|
|
Соответствия между множествами. Взаимно однозначные соответствия.ГЛАВА 1 СООТВЕТСТВИЯ. ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА СООТВЕТСТВИЯ МЕЖДУ МНОЖЕСТВАМИ Множества и операции над ними Основными неопределяемыми понятиями математики являются «множество», «элемент множества». Множества представляют собой совокупность каких-либо предметов (объектов), обладающих общим свойством. Эти объекты бывают разной природы: числовые, геометрических фигур, людей и т.д. Договоримся называть их «элементами множества». Множества принято обозначать большими буквами латинского алфавита А,В, С,…, Х, У, Z, а элементы множеств – маленькими буквами латинского алфавита a, b, c, …, x, y, z. Если некоторый объект a является элементом некоторого множества A, то говорят, что «элемент а принадлежит множеству А» и обозначают а А= {x| свойство, которым обладают все элементы}. В нашем курсе мы будем изучать в основном числовые множества. Далее будем использовать следующие кванторы · · и общепринятые математические символы вместо слов: · А · А · ˄ знак конъюнкции, заменяет союз «и» · ˅ знак дизъюнкции, заменяет союз «или» Множества могут находиться или не в следующих отношениях: ü пересечения – множества А и В находятся в отношении пересечения (А∩В), если существуют элементы, принадлежащие и одному и другому множествам одновременно и существуют элементы, принадлежащие только множеству А и только множеству В; ü включения – множества А и В находятся в отношении включения, если каждый элемент множества А принадлежит множеству В, говорят, что множество А является подмножеством множества В и обозначают AÌB; ü равенства – множества A и B называются равными (A = B), если они состоят из одних и тех же элементов. Следствия 1.1. Каждое множество является подмножеством самого себя: A Ì А. 1.2. Пустое множество является подмножеством любого множества A: Æ Ì A. Множества A и Æ называют несобственными подмножествами множества A, все остальные – собственными подмножествами множества A. Операции над множествами Пусть А и В — некоторые множества. Определение 1.1. Объединением двух множеств А и В называется множество, состоящее из тех и только тех элементов, которые принадлежат хотя бы одному из этих множеств. Обозначается: АÈВ. На рис. 1 показано объединение множеств А и В при помощи диаграммы Эйлера–Венна. Рис. 1 Прежде, чем рассмотреть примеры объединения множеств, заметим, что согласно определению объединения х Î А È В Û х Î А ˅ х Î В. Свойства объединения множеств Из определения следует, что в А È А входят те же самые элементы, т.е. А È А = А. Вообще, когда B Ì A, то А È В = А. В частности, А È Æ = А. Операция объединения подчиняется переместительному закону: А È В = В È А. Операцию объединения можно распространить на любое число множеств. Когда А, В, С — три произвольные множества, то (А È В)È С есть множество элементов, каждый из которых принадлежит хотя бы одному из множеств А, В, С. В общем случае объединение совокупности множеств Операция объединения подчиняется сочетательному закону: (А È В)È С = А È (В È С). Определение 1.2. Пересечением множеств A и B называется множество, состоящее их тех и только тех элементов, которые одновременно принадлежат множествам A и B. Обозначается: АÇВ. Согласно определению пересечения х Î АÇ В Û х Î А ˄ х Î В. Пересечение множеств А и В иллюстрируется на рис. 2. Рис. 2 Свойства пересечения множеств Очевидно, что А Ç А = А; вообще, когда В Ì А, то В Ç А = В. Из определения пересечения следует: А Ç В = В Ç А, т.е. операция пересечения коммутативна. Имеет место и следующее равенство: А Ç Æ = Æ. Операцию пересечения легко распространить и на случай больше двух множеств. Рассмотри три множества А, В, С. Пересечение А Ç В есть множество общих элементов множеств А и В, поэтому (А Ç В) Ç С есть множество элементов, принадлежащих одновременно трём множествам А, В, С. Аналогично определяется и операция пересечения любого числа множеств. Из приведенного правила пересечения трех множеств следует, что операция пересечения ассоциативна: (А Ç В) Ç С = А Ç (В Ç С). Поэтому используется запись А Ç В Ç С. В общем случае пересечение совокупности множеств Заметим, что относительно двух операций пересечения и объединения множеств выполняются два дистрибутивных (распределительных) закона: 1) (А Ç В) È С = (А È С) Ç (В È С); 2) (А È В) Ç С = (А Ç С) È (В Ç С). Докажем второй из этих законов (первый доказывается аналогично). Пусть х Î (А È В) Ç С. Значит, х Î А È В и х Î С. Из того, что х Î А È В, следует, что обязательно выполняется по крайней мере одно из двух утверждений: х Î А или х Î В. Когда х Î А, то из того, что х Î С, следует, что х Î А Ç С. Значит, х Î (А Ç С) È (В Ç С). Когда же х Î В, то из того, что х Î С, следует, что х Î В Ç С, но тогда х Î (А Ç С) È (В Ç С). Таким образом, любой элемент множества (А È В) Ç С является элементом и множества (А Ç С) È (В Ç С). Докажем теперь обратное. Пусть х Î (А Ç С) È (В Ç С). Возможен один из случаев: х Î А Ç С или х Î В Ç С, т.е. х Î А и х Î С, или х Î В и х Î С. Отсюда получаем, что х Î С и х Î А È В, а это свидетельствует о том, что х Î (А È В)Ç С. Таким образом, второй дистрибутивный закон доказан полностью. Определение 1.3. Разностью двух множеств A и B называется множество, состоящее из тех и только тех элементов, которые принадлежат A и не принадлежат В. Обозначается: А \ В. Согласно определению разности х Î А \ В Û х Î А ˄ х Ï В. Графическое изображение разности А \ В множеств А и В показано на рисунке 3 (заштрихованная область — это А \ В). Рис. 3 Из определения разности следует, в частности, что А \ А = Æ; А \ В ¹ В \ А. Определение 1.4. Если множество B является подмножеством множества A, то разность множеств A и B называется дополнением множества B до множества A. Обозначается: А \ В=САВ или Графическое изображение дополнения Рис. 4 Соответствия между множествами. Взаимно однозначные соответствия. Основным объектом математического анализа является «функция». Введем это понятие через понятие «соответствие». Пусть заданы два множества X и Y. Если для каждого элемента а Î Х указан (один, или несколько, или ни одного) элемент b Î Y, с которым сопоставляется а, то говорят, что между множествами X и Y установлено соответствие (бинарное отношение). В основе понятия «соответствия» лежит «упорядоченная пара» (короче «пара»). Определение 1.5. Упорядоченной парой называется множество, состоящее из двух элементов, для которых указан порядок следования. Обозначают (х;у); элемент х называют первой компонентой (координатой), у – второй компонентой (координатой) пары. Основное свойство пары: две пары равны Не следует путать множество {х;у} и пару (х;у): (х;у) Определение 1.6. Упорядоченной тройкой (тройкой) называется пара ((х;у), z), первая координата которой – пара (х;у), а вторая – z . Обозначают (х;у; z). Аналогично определяются упорядоченные четвёрки, пятёрка, и т. д. n-ки. Определение 1.7. Декартовым (прямым) произведением множеств Х и Y называется множество, состоящее из всех возможных пар (х;у), где C помощью символов это определение можно записать так:
Пример 1.1. Пусть Х = {1, 2, 3}, Y = {k, l}. Найти Х ´ Y и Y ´ Х. Решение. Декартовое произведение Х ´ Y состоит из шести элементов: Х ´ Y = {(1, k), (2, k), (3, k), (1, l), (2, l), (3, l)}. Выпишем теперь декартовое произведение Y ´ Х = {(k, 1), (k, 2), (k, 3), (l, 1), (l, 2), (l, 3)}. Таким образом, Х ´ Y ¹ Y ´ Х (не выполняется ассоциативный закон). Результат декартового произведения зависит от порядка сомножителей. Принято считать, что для любого множества Х справедливы равенства: · · Множество Если множества X и Y – числовые, то пары элементов (x; y) можно рассматривать как координаты точек на плоскости. В этом случае декартово произведение можно изобразить в декартовой системе координат. Определение 1.8. Любое подмножество декартового произведения множеств Будем обозначать соответствия маленькими буквами латинского f, g,.. и греческого φ, ψ… алфавитов. Множество всех первых компонент пар из соответствия f называют областью определения соответствия f, а множество всех вторых компонент пар из соответствия f называют областью значения соответствия f, и обозначают, соответственно D(f) и E(f). Пусть f – соответствие между множествами Х и Y. Если Пример 1.2.Между элементами множеств X = {2, 3, 5, 11} и Y = {6, 7, 9, 10} задано соответствие f : «число x является делителем числа y». Очевидно, что множество f ={(2, 6), (2, 10), (3, 6), (3, 9), (5, 10)} – пар элементов, находящихся в заданном отношении, является подмножеством декартова произведения множеств X´Y = {(2, 6), (2, 7), (2, 9), (2, 10), (3, 6), (3, 7), (3, 9), (3, 10), (5, 6), (5, 7), (5, 9), (5, 10), (11, 6), (11, 7), (11, 9), (11, 10)}. Полным образом элемента a из множества X называется множество всех элементов из Y, которые соответствуют элементу а. Обозначают f(а). В частности, для примера 1 f(2)={6, 10}, f(3)={6, 9}, f(5)={10}, f(11)= Æ . Полным прообразом элемента b из множества Y называется множество всех элементов из Х, которым b соответствует. Обозначают f –1(b). В частности, для примера 1.2 f –1 (6)={2, 3}, f –1 (7)= Æ, f –1 (9)={3}, f –1 (10)= {2, 5} . Множество всех элементов из X, имеющих непустые образы, называется множеством (областью) определения соответствия, и обозначают D(f), а множество всех элементов из Y, имеющих непустые прообразы – множеством (областью) значений соответствия и обозначают Е(f). Так, в примере 1.2 область определения соответствия f есть множество D(f) ={2, 3, 5}, а множество значений соответствия f есть множество Е(f) = {6, 9, 10}. Если множества X и Y совпадают, то говорят об отношении между элементами множества X. Замечание 1.1. Соответствие между множествами можно задавать а) перечислением пар б) таблицей
в) графами
г) с помощью графика (если множества числовые) Соответствия могут быть различных видов. Приступим к их изучению. Пусть f соответствие между элементами множеств X и Y. Соответствие f называется всюду определенным, если множество D(f) = Х. Если E(f) = Y. Если же E(f) = Y, то соответствие называют сюръективным. На рис. 5 а и 5 б представлено всюду определенное сюръективное соответствие. Соответствия, представленные на рис. 5 в и 5 г, не сюръективны, а соответствие, изображенное на рис. 5 г, не всюду определенное. Рис. 5 Соответствие называется инъективным, если любой элемент из E(f) соответствует единственному элементу из D(f). На рис. 5 а изображено инъективное соответствие. Особое место занимают функциональные соответствия. Определение 1.9. Соответствие f между множествами Х и Y, при котором каждому Определение 1.10. Если область определения функции f состоит из некоторого множества действительных чисел, то f называется функцией одной действительной переменной. Если область определения функции f состоит из упорядоченных n-ок действительных чисел, то f называется функцией n действительных переменных. Если область значений функции f состоит из некоторого множества действительных чисел, то f называется действительной функцией. Пример 1.3.Среди соответствий, изображенных на рис. 6, функциями будут f и p. Их областями определения будут, соответственно, D(f) = {a, b, c}, D(p) = {a, b, c}, а множествами значений E(f) = {1, 3}, E(p) = {1, 2, 3}. Если
Определение 1.7. Соответствие между элементами множеств Х и Y, при котором каждому элементу множества Х соответствует единственный элемент множества Y, и каждый элемент множества Y соответствует только одному элементу из множества Х, называется взаимно однозначным(или биективным). Определение 1.8. Множества Х и Y называются эквивалентными, или равномощными, если между ними каким-либо способом можно установить взаимно однозначное соответствие. Эквивалентность двух множеств обозначается так: X ~ Y. Пусть задано соответствие f между множествами X и Y. Обратным ему называется соответствие f –1между множествами Y и X, состоящее из таких пар (у; х), для которых верно, что (х; у) ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА Из СШ известны следующие обозначения: N – множество натуральных чисел, Z – множество целых чисел, Z0 – множество целых неотрицательных чисел, Q – множество рациональных чисел, I – множество иррациональных чисел, R – множество действительных чисел. В курсе СШ под действительным числом понимают бесконечную десятичную дробь без 9 в периоде. Если бесконечная десятичная дробь – периодическая, то это рациональное число, а если бесконечная десятичная дробь – непериодическая, то это иррациональное число. Из курса математики СШ известно, что множество, состоящее и рациональных и иррациональных чисел, называется множеством действительных чисел (R). На множестве R вводятся операции «сложения», «умножения», отношение порядка (сравнение). Формулируются 3 группы аксиом: I. Аксиомы сложения и умножения 1. a+ b = b + a 2. a+ (b + c )= (a + b) + c 3. a ∙ b = b ∙ a 4. a ∙ (b ∙ c )= (a ∙ b) ∙ c 5. (a + b) ∙ c= a ∙ c + b ∙ c 6. Существует число 0 такое, что а + 0 = а для любого действительного числа а 7. Для любого действительного числа а существует число – а такое, что а + (– а) = 0 8. Существует число 1≠0 такое, что а ∙ 1 = а для любого действительного числа а 9. Для любого действительного числа а≠0существует число а –1 такое, что а ∙ а –1 = 1 II. Аксиомы порядка Для любых 1. Для любых 2. Если 3. Если 4.Если х≤у, то для любого z выполняется х + z ≤ у + z 5.Если х≤у, то для любого z > 0 выполняется х ∙ z ≤ у ∙ z, а для любого z < 0 выполняется х ∙ z ≥ у ∙ z. III. Аксиома непрерывности.Пусть X и Y два непустых множества действительных чисел. Если Все остальные свойства можно получить из этих аксиом. Такой подход к определению множества действительных чисел называется аксиоматическим, действительные числа – это множество, элементы которого удовлетворяют аксиомам групп I–III. Между множеством действительных чисел и точками любой прямой можно установить взаимно однозначное соответствие. Рассмотрим любую прямую и отметим на ней произвольно точку 0 – начало отсчёта. Точка 0 разбивает данную прямую на два луча. Один из них назовём положительным и обозначим стрелкой, а другой отрицательным. От точки 0 отложим на положительном луче произвольный отрезок и назовём его единичным (его длину примем за единицу измерения длин). Из СШ известно, что прямая, с выбранным на ней началом отсчёта 0, положительным направлением и единичным отрезком, называется координатной прямой. Возьмем произвольное действительное число х. Возможны случаи: 1) x>0. Отложим на положительном луче координатной прямой от точки 0 отрезок длины x. Правый конец полученного отрезка – соответствующая x точка. 2) x<0. Отложим на отрицательном луче координатной прямой от точки 0 отрезок длины (– x). Левый конец полученного отрезка – соответствующая x точка. 3) x=0, соответствующая ему точка – точка 0. Таким образом, установили взаимно однозначное соответствие между множеством действительных чисел и точками координатной прямой. Поэтому в математике принято множество R (действительных чисел) называть числовой прямой, а его элементы, т.е. действительные числа, точками числовой прямой. Часто для наглядности вместо действительного числа х рассматривают ту точку на координатной прямой, которая соответствует этому действительному числу. Эту точку называют геометрическим изображением числа х и обозначают так же через х.
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
А. Таким образом, множества состоят из элементов и в зависимости от их числа бывают конечными и бесконечными, пустыми (Æ). Для записи множеств используют фигурные скобки, в которых через запятую перечисляются все элементы. Но если множество бесконечное, то перечислить все его элементы мы не сможем. В таких случаях мы будем использовать такую запись:
общности вместо слов «для любых» или «для всех (каждого)»
существования вместо слов «существует» или «есть»
В «если А, то В» или «из А следует В»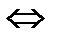
В «А тогда и только тогда, когда В» или «А равносильно В»
обозначается 
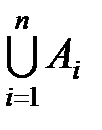и состоит из элементов, принадлежащих хотя бы одному из множеств 
.
и состоит из элементов, принадлежащих сразу всем множествам 
, 
.
или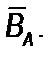 
множества В до множества А показано на рис. 4.
(у;х), а {х;у}={у;х}.
, 
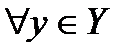и обозначают 
.
;
.
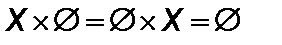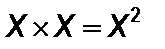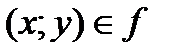, то говорят, что «при соответствии f элемент x соответствует элементу y». В этом случае элемент у называется образом элемента х, а элемент x – прообразом элемента y при соответствии f.
соответствует один и только один 
называется функциональным (функцией). Элемент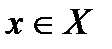 
называется аргументом функции f, а соответствующий ему элемент 
или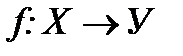 
f. Соответствия f и f –1 называют взаимно обратными.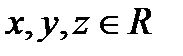
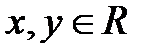либо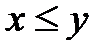 
, либо 
.
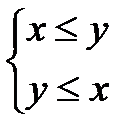, то x=y.
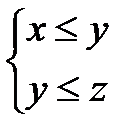, то 
.
выполняется неравенство 
, такое, что 