
|
|
Операция замыкания и предполные классыЗамыканием множества М ÍР2, обозначается [M], называется множество всех булевых функций, полученных суперпозициями из М. Основные свойства замыкания:
Например, [{&,®,Ø}]=P2, так как согласно доказанной ранее теореме произвольная булева функция может быть представлена булевой формулой. Замыкание одноэлементного множества {
Таким образом, замыкание рассматриваемого множества содержит ровно две функции: тождественную функцию х и саму функцию отрицания Замыкание двухэлементного множества {0,1} не содержит никаких новых функций кроме констант 0 и 1, поскольку это нульместные функции и никакие подстановки не возможны. Поэтому [{0,1}]={0,1}; Замыкание двухэлементного множества
Тогда Пусть МÍР2. Операция получения множества [M] из М называется операцией замыкания. Множество М называется функционально замкнутым классом, если [M]=M. Множество всех булевых функций является функционально замкнутым классом. Пусть М – замкнутый класс в Р2. DÌM называется функционально полной системой в М, если [D] = M. Множество D называется неприводимой системой, если замыкание любого его собственного подмножества отлично от замыкания D. Например, множество Функции f1 и f2 называются конгруэнтными, если одна из них может быть получена из другой заменой переменных (без отождествления). Например, функции Множество функций QÍР2 называется предполным классом, если [Q]ÌP2, и Теорема. Предполный класс замкнут. Доказательство от противного. Пусть В математической логике рассматривается пять предполных классов. Класс функций, сохраняющих 0, Т0 Определение функции, сохраняющей 0:
Пусть функция Приведенное выше рассуждение, определяющее мощность класса Т0 означает замкнутость класса. Докажем это явно. Пусть имеется множество
Элементарные булевы функции f(x1,x2,…,xn)ÎT0(n)Ûf(0,0,…,0)=0. T0= Лемма о функции, не сохраняющей 0: Если fÏТ0, то отождествлением ее переменных или подстановкой функций, сохраняющих 0, из нее можно получить константу 1 или функцию отрицания Øх. Пример. Получим константу 1 и функцию отрицания из импликации.
Класс функций, сохраняющих 1, Т1 f(x1,x2,…,xn)ÎP2(n) Û f(1,1,…,1)=1.
Доказательство замкнутости класса Т1 аналогично доказательству замкнутости класса Т0. Мощность класса T1(n)=|P2(n)|/2. Неполнота класса Т1 следует из существования функций, не сохраняющих 1. Лемма о функции, не сохраняющей 1: Если fÏТ1, то отождествлением ее переменных или подстановками функций, сохраняющих 1, из нее можно получить константу 0 или функцию отрицания Øх. Пример. Получим константу 0 и функцию отрицания из функции Å. Тождественная функция и константа 1 сохраняют 1 и, следовательно, могут участвовать в подстановках при доказательстве. Произведем отождествление переменных, т.е. подстановку переменной x в формулу:
Следующая подстановка позволяет получит функцию отрицания.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
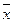 } определим единственной возможной подстановкой:
} определим единственной возможной подстановкой:
 .
. может быть получено подстановками:
может быть получено подстановками: и
и 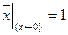 .
. .
. , а множества
, а множества  и {0} не являются.
и {0} не являются. и
и  - конгруэнтные, а функции x&y и z&z – нет.
- конгруэнтные, а функции x&y и z&z – нет. .
. и пусть имеется функция
и пусть имеется функция  . Тогда
. Тогда  . Но
. Но  , следовательно,
, следовательно,  т.е.
т.е. 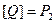 , что противоречит определению предполного класса. Следовательно, такой функции не существует, т.е. предполный класс замкнут.
, что противоречит определению предполного класса. Следовательно, такой функции не существует, т.е. предполный класс замкнут. .
. сохраняет 0. Тогда на нулевом наборе значений переменных значение функции равно 0, а на всех остальных наборах значений переменных функция может принимать произвольные значения. Поскольку число строк таблицы равно 2n, то число строк, на которых функция может принимать произвольные значения равно 2n-1, число n-местных булевых функций, сохраняющих 0, равно числу слов длины 2n-1 в двоичном алфавите, те равно числу размещений с повторениями из 2 по 2n-1. Таким образом, число n-местных булевых функций, сохраняющих 0 равно половине от числа всех n-местных булевых функций. |T0(n)|=
сохраняет 0. Тогда на нулевом наборе значений переменных значение функции равно 0, а на всех остальных наборах значений переменных функция может принимать произвольные значения. Поскольку число строк таблицы равно 2n, то число строк, на которых функция может принимать произвольные значения равно 2n-1, число n-местных булевых функций, сохраняющих 0, равно числу слов длины 2n-1 в двоичном алфавите, те равно числу размещений с повторениями из 2 по 2n-1. Таким образом, число n-местных булевых функций, сохраняющих 0 равно половине от числа всех n-местных булевых функций. |T0(n)|=  .
. . Покажем, что произвольная суперпозиция этих функций также будет сохранять 0. Пусть суперпозиция
. Покажем, что произвольная суперпозиция этих функций также будет сохранять 0. Пусть суперпозиция  получена подстановкой функций из заданного множества вместо аргументов функции F. Очевидно, что на нулевом наборе значений переменных каждая из функций суперпозиции обращается в 0. В свою очередь
получена подстановкой функций из заданного множества вместо аргументов функции F. Очевидно, что на нулевом наборе значений переменных каждая из функций суперпозиции обращается в 0. В свою очередь  Следовательно, суперпозиция функций, сохраняющих 0 также сохраняет 0. Т.е. класс функций, сохраняющих 0, замкнут и включает функции всех возможных арностей: T0=
Следовательно, суперпозиция функций, сохраняющих 0 также сохраняет 0. Т.е. класс функций, сохраняющих 0, замкнут и включает функции всех возможных арностей: T0=  . Способ построения таблицы всех n-местных булевых функций подтверждает, что
. Способ построения таблицы всех n-местных булевых функций подтверждает, что .
. сохраняют 0. Функция отрицания
сохраняют 0. Функция отрицания  . Неполнота класса Т0 следует из существования функций, не сохраняющих 0.
. Неполнота класса Т0 следует из существования функций, не сохраняющих 0. .
. .
. .
. , а
, а  .
.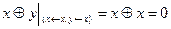 . Отождествлением переменных получили константу 0.
. Отождествлением переменных получили константу 0. .
.