
|
|
Элементарные булевы функцииБулевы векторы и единичный n-мерный куб Множество На множестве вершин единичного n-мерного куба задаются следующие характеристики: · Вес вектора, равный · Номер вектора, равный десятичному числу, записанному в двоичной системе счисления: · Расстояние Хемминга между двумя булевыми векторами, равное числу разрядов, в которых эти векторы различаются, определяемое как · На множестве булевых векторов длины n определено отношение предшествования: Функции алгебры логики (булевы функции) n-местной булевой функцией называется отображение Множество всех n-местных булевых функций равна Переменная Двойственные функции Функция
Соответствующие таблицы представлены ниже.
Примеры элементарных двойственных функций:
Очевидно выполнение тождественного равенства
Элементарные булевы функции Элементарными булевыми функциями называются функции с арностью 0, 1 и 2. При этом нужно заметить, что множество функций двух переменных включают в себя все 0-местные и 1-местные функции, в описании которых присутствует две или одна фиктивная переменная соответственно. Множество всех элементарных булевых функций может быть представлено в виде таблицы, содержащей 4 строки и 16 столбцов. Каждый столбец определяет одну из элементарных булевых функций. Наиболее употребимыми являются двуместные функции: {&,Ú,®,«,Å,ê,¯}, одноместные функции f(x)=x и f(x)=`x, и две 0-местные функции: константа 0 и константа 1, не имеющие ни одной существенной переменной (других таких функций в множестве элементарных булевых функций нет). Элементарные булевы функции используются для аналитического задания булевых функций произвольной местности формулами. При этом используется принцип суперпозиции функций. Согласно этому принципу формула определяется индуктивно: · Пропозициональная переменная есть формула. · Если А и В формулы, то любое слово А·В – формула, если ·Î{&,Ú,®,«,Å,ê,¯}. Слово `А также является формулой. · Других формул нет. Для формулы может быть построена таблица истинности, которая является ее интерпретацией. Говорят, что пропозициональная формула задает булеву функцию. Соответственно, булева функция реализует ту формулу, которая задает функцию. Очевидно, формула задает единственную булеву функцию. Обратное не справедливо. Формулы, определяемые суперпозицией функций, могут преобразовываться как алгебраические выражения с использованием множества аксиом и тождеств. Основными из них являются аксиомы тождественности (идемпотентности), коммутативности, ассоциативности, дистрибутивности, поглощения, закон двойного отрицания, правило де-Моргана. Целью преобразования формул является приведение их к каноническому виду. В теории булевых функций используются канонические представления: дизъюнктивная нормальная форма (ДНФ), конъюнктивная нормальная форма (КНФ), полиномиальная нормальная форма. (ПНФ). Для выполнения преобразований используется правило подстановки, которое формулируется следующим образом: если формула образована суперпозицией функций над некоторым множеством функций, то замена вхождения какой-либо функции на равносильную ей не меняет логическое значение функции. Это можно представить как 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 называется единичным n-мерным кубом. Упорядоченная последовательность (кортеж) длины n называется вершиной единичного n-мерного куба. Мощность множества вершин единичного n-мерного куба равна
называется единичным n-мерным кубом. Упорядоченная последовательность (кортеж) длины n называется вершиной единичного n-мерного куба. Мощность множества вершин единичного n-мерного куба равна  .
. ;
; если разряды двоичного вектора нумеруются справа налево, начиная с 0, т.е.
если разряды двоичного вектора нумеруются справа налево, начиная с 0, т.е.  .
. . Два вектора
. Два вектора  называются соседними, если расстояние Хемминга между ними равно 1, и противоположными, если расстояние Хемминга между ними равно n.
называются соседними, если расстояние Хемминга между ними равно 1, и противоположными, если расстояние Хемминга между ними равно n. . Нетрудно доказать, что отношение предшествования является отношением частичного порядка на множестве вершин единичного n-мерного куба.
. Нетрудно доказать, что отношение предшествования является отношением частичного порядка на множестве вершин единичного n-мерного куба. , где n-местность (арность) функции. Это отображение может быть иначе записано как
, где n-местность (арность) функции. Это отображение может быть иначе записано как  . Переменные
. Переменные  называются пропозициональными переменными.
называются пропозициональными переменными. . n-местная булева функция может быть представлена таблицей, содержащей
. n-местная булева функция может быть представлена таблицей, содержащей  строк, расположенных по возрастанию сверху вниз номера строки. Таким образом, вектор n-местной булевой функции имеет длину
строк, расположенных по возрастанию сверху вниз номера строки. Таким образом, вектор n-местной булевой функции имеет длину  , а множество вершин, в которых функция принимает значение 0,
, а множество вершин, в которых функция принимает значение 0, 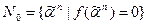 , то очевидно, что
, то очевидно, что  . Для задания полностью определенной булевой функции достаточно указать одно из этих множеств.
. Для задания полностью определенной булевой функции достаточно указать одно из этих множеств.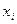 называется существенной, если выполняется условие:
называется существенной, если выполняется условие:  , т.е. существует хотя бы одна пара наборов, соседних по переменной
, т.е. существует хотя бы одна пара наборов, соседних по переменной 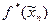 , определенная как отрицание функции
, определенная как отрицание функции  от отрицания ее аргументов называется двойственной функции
от отрицания ее аргументов называется двойственной функции  . Согласно определению таблица двойственной функции получается инвертированием столбца функции
. Согласно определению таблица двойственной функции получается инвертированием столбца функции  .
.

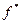
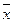
 .
. , если
, если  с точностью до фиктивных переменных.
с точностью до фиктивных переменных.