
|
|
Найдем взаимную корреляционную функцию по свойству 7) п.8
10. Дана корреляционная функция kX (τ) стационарного с. п. X(t). Найти корреляционную функцию
а) kX (τ)= 72/(1+9τ 2). б) kX (τ)= Решение. а) Обозначим
Подставив эту функцию в (5), получим
Найдем дисперсию свойству 10) п. 8:
Найдем взаимную корреляционную функцию по свойству 11) п. 8
б) При t ³ 0 имеем По формуле (5) имеем
=
При условии 0 £ t2£ t1 по формуле 11) п.8 имеем
Заметим, что это вычисление верно и при более слабых условиях: t2 £ t1, 0£ t1. 11. kX (τ) - корреляционная функция стационарного с. п. X(t). Найти его спектральную плотность. а) kX (τ)= б) kX (τ)= 12exp(-4|τ|)(1+4|τ|). Решение. а) Воспользуемся формулой (10) п. 10.
По формуле 15 приложения 1 при a = 4, m = w имеем
б) По формуле (10) п. 10 имеем
Первый из этих интегралов вычислим по формуле 19, а второй - по формуле 20 приложения 1:
12. Найти корреляционную функцию стационарного с. п. X(t), если его спектральная плотность а) SX (w) = б) SX (ω) = Решение. а) Воспользуемся формулой (11) п. 10
Для нахождения интеграла
если t ¹0. При t =0 получим
б) Воспользуемся формулой (9) п. 10
При t ³ 0 эти интегралы вычислим при помощи вычетов по формуле (4) приложения 2. Сначала найдем полюсы подынтегральных функций с положительной мнимой частью: 4 + (3 - ω)2 = 0 ═> ω1 = 3 + 2i, 4 + (3 + ω)2 = 0 ═> ω2 = -3 + 2i. Имеем
Вычеты вычислим по формуле (1) приложения 2
Из-за четности функции kX (τ) при всех
13. На вход стационарной линейной динамической системы, описываемой дифференциальным уравнением y″ + 8y′+ 15y =5x′ +10x, подается стационарный случайный процесс X(t) с математическим ожиданием mX = 5и спектральной плотностью SX (ω) = sin7ω/ω. Найти математическое ожидание и дисперсию случайного процесса Y(t) на выходе системы в установившемся режиме. Решение. По формуле 1) п. 11 найдем математическое ожидание
Дисперсию будем вычислять по формуле 2) п. 11:
Сначала составим передаточную функцию
Затем найдем амплитудно-частотную характеристику системы
Подставив это выражение в формулу дисперсии, получим
Для вычисления этого интеграла разложим амплитудно-частотную характеристику на сумму простейших дробей.
Таким образом,
Каждый из этих интегралов вычислим по формуле 8 приложения 1 (в первом интеграле положим m = 7, a =3, во втором - m = 7, a = 5):
14. На вход стационарной линейной динамической системы, описываемой дифференциальным уравнением y″+ 4y′+ 4y =5x′, подается стационарный случайный процесс X(t) с корреляционной функцией kX (τ)=16exp(-4|τ|)cos3τ. Найти спектральную плотность SY (ω) случайного процесса Y(t) на выходе системы в установившемся режиме. Решение. Сначала найдем спектральную плотность с. п. X(t) по формуле (10) п. 10
По формуле 22 приложения 1 при a = 4, m =3, n = ω имеем
Найдем передаточную функцию и амплитудно-частотную характеристику
Наконец, по формуле 3) п. 11 получим
15. На вход стационарной линейной динамической системы, описываемой данным дифференциальным уравнением, подается стационарный с. п. X(t) со спектральной плотностью SX (ω). Найти корреляционную функцию kY (τ) с. п. Y(t) на выходе системы в установившемся режиме. а) б)
Решение. а) Воспользуемся формулой 4) п. 11.
Найдем амплитудно-частотную характеристику системы
Во втором интеграле сделаем замену
Последний интеграл вычислим по формуле (4) приложения 2. Найдем все полюса подынтегральной функции с положительными мнимыми частями: ω2 +1= 0 ═>ω0 = i , 4 + (3 -ω)2 = 0 ═> ω1 = 3 + 2i. Все они являются простыми полюсами.
Таким образом,
Из-за четности функции kX(τ) при всех действительных значениях τ получаем
б) Найдем амплитудно-частотную характеристику системы
По формуле 4) п. 11 получаем
Дробь в подынтегральном выражении разложим на сумму простейших дробей методом неопределенных коэффициентов.
Приравняем числители:
Решив ее, найдем
В случае t ³ 0 первые два интеграла вычислим по формуле 1, а третий – по формуле 11 из приложения 1.
Из-за четности функции kY (τ) при всех действительных значениях τ имеем
ПРИЛОЖЕНИЕ 1 Табличные интегралы
ПРИЛОЖЕНИЕ 2

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 =
= 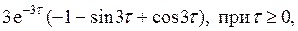
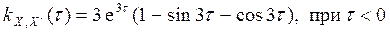
 , дисперсию
, дисперсию  случайного процесса
случайного процесса  , взаимную корреляционную функцию kX,Z (t1, t2) (в случае б) –лишь при 0 £ t2£ t1 )
, взаимную корреляционную функцию kX,Z (t1, t2) (в случае б) –лишь при 0 £ t2£ t1 ) .
. . Тогда по формуле (5) п. 8 имеем
. Тогда по формуле (5) п. 8 имеем .
.
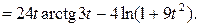
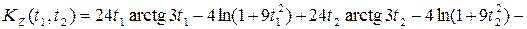

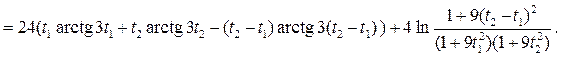
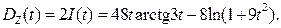
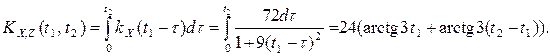
 (интеграл вычислен по частям).
(интеграл вычислен по частям). =
=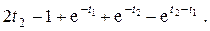
 .
.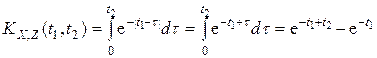 .
.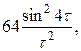
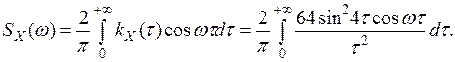
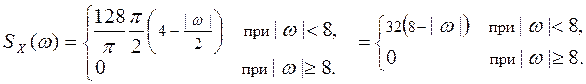
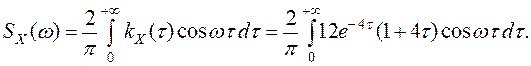
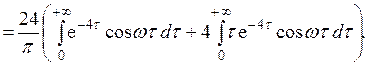
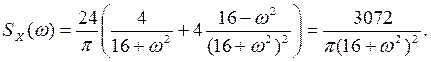

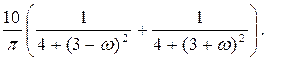
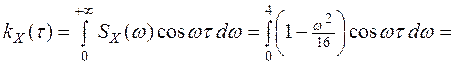

 воспользуемся формулой 25 приложения 1.
воспользуемся формулой 25 приложения 1.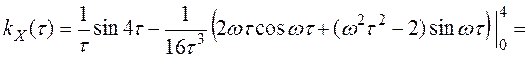
 ,
,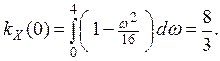
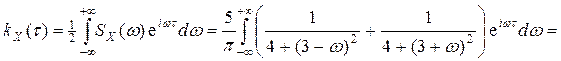
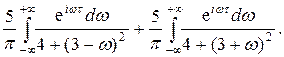
 .
.
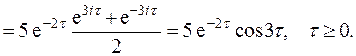
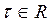 получаем
получаем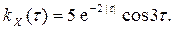
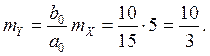
 .
.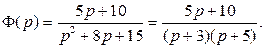
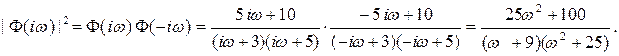
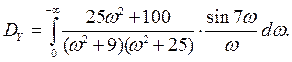
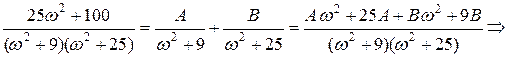
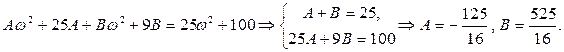
 и, следовательно,
и, следовательно,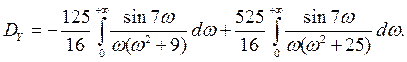


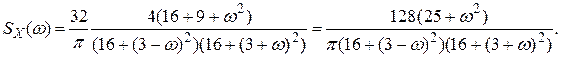

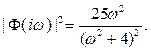
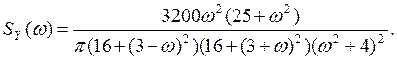
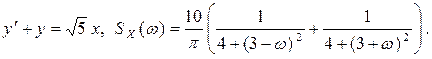

 .
.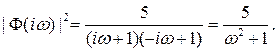
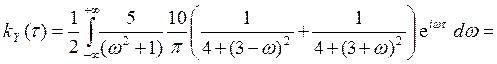

 Тогда
Тогда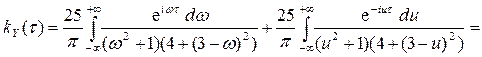
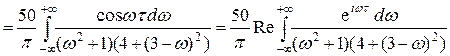 .
.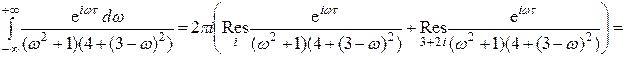
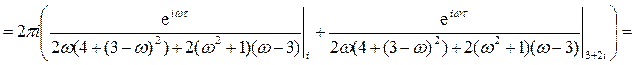
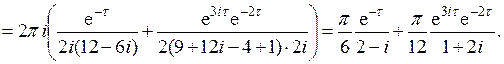


 .
.
 .
.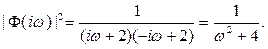
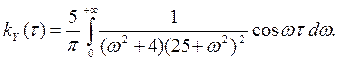
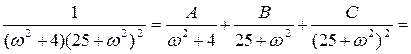
 .
. Подставляя в это уравнение поочередно значения ω = 0, ω = 5i, ω = 2i, получим систему уравнений
Подставляя в это уравнение поочередно значения ω = 0, ω = 5i, ω = 2i, получим систему уравнений
 Таким образом,
Таким образом,
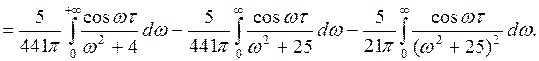

 .
. 

 .
. , a > 0, m ≥ 0.
, a > 0, m ≥ 0.
 a > 0, m ≥ 0.
a > 0, m ≥ 0.
 a > 0, m ≥ n ≥ 0.
a > 0, m ≥ n ≥ 0.
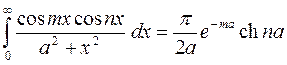 , a > 0, m ≥ n ≥ 0.
, a > 0, m ≥ n ≥ 0.

 , a ≥ 0, m > 0.
, a ≥ 0, m > 0.
 a > 0, m ≥ 0.
a > 0, m ≥ 0.
 , a > 0, m ≥ 0.
, a > 0, m ≥ 0.
 a > 0, m ≥ 0.
a > 0, m ≥ 0.
 , a > 0, m ≥ 0.
, a > 0, m ≥ 0.
 , a > 0, m ≥ 0
, a > 0, m ≥ 0
 , a, b>0, m≥0, a ≠ b.
, a, b>0, m≥0, a ≠ b.
 , a, b>0, m≥0, a ≠ b.
, a, b>0, m≥0, a ≠ b.



 , a > 0.
, a > 0.
 a > 0.
a > 0.
 a > 0.
a > 0.
 a > 0.
a > 0.
 , a > 0.
, a > 0.
 , a > 0.
, a > 0.
 , a > 0.
, a > 0.
 a ≠ 0.
a ≠ 0.
 , a ≠ 0.
, a ≠ 0.
 a ≠ 0.
a ≠ 0.
 a ≠ 0.
a ≠ 0.