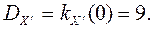|
|
Корреляционная функция с.п.Пусть Корреляционной функцией с.п. X(t) называется неслучайная функция от двух аргументов t1, t2
Нормированной корреляционной функцией с.п. X(t) называется неслучайная функция
Свойства корреляционной функции с.п. Пусть X(t) - случайный процесс, U - случайная величина, φ(t) - неслучайная функция.
1) 2) 3) 4) 5) 6) 7) 8)
5. Взаимная корреляционная функция с.п.Пусть X(t), Y(t) - случайные процессы. Взаимной корреляционной функцией с. п. X(t), Y(t) называется неслучайная функция от двух аргументов t1, t2
Два с.п. X(t), Y(t) называются некоррелированными, если
Нормированной взаимной корреляционной функцией с.п. X(t), Y(t) называется неслучайная функция
Свойства взаимной корреляционной функции. Пусть X(t), Y(t) - случайные процессы, φ(t), ψ(t) - неслучайные функции.
1) 2) 3) 4) 5) 6) Теорема. Если
Следствие. Если
Для двух случайных процессов
Если с.п.
6. Характеристики производной случайного процесса.Пусть X(t) - случайный процесс, 1) 2) 3) Замечание. Рекомендуем ознакомиться с понятиями предела, производной и интеграла в среднеквадратическом смысле в пособиях /2,5,8/.
7. Характеристики интеграла от случайного процесса. Пусть X(t) - случайный процесс,
Тогда выполняются следующие свойства. 1) 2) 3)
Стационарные случайные процессы. С.п. X(t) называется стационарным (в широком смысле), если его м. о. постоянно, а корреляционная функция зависит только от Таким образом,
Два стационарныхс.п. X(t) и Y(t) называются стационарно связанными, если взаимно корреляционная функция
Основные свойства и формулы для стационарных с.п.Пусть X(t) - стационарныйслучайный процесс. 1) 2) 3) 4)
Характеристики производной стационарного случайного процесса.Пусть X(t) - дифференцируемый стационарный с.п. Тогда
5) 6) 7) 8) Характеристики интеграла от стационарного случайного процесса.Пусть X(t) - интегрируемый стационарный с.п. и 9) 10) 11) Рассмотрим функцию
Заметим, что функция I(t) – четная, а для функции
Эргодическое свойство стационарного случайного процесса. Определение. Стационарный с.п. X(t) называется эргодическим относительно математического ожидания mX , если для любой его реализации
Стационарный с.п X(t) называется эргодическим относительно корреляционной функции kX(τ), если для любой его реализации
Спектральное разложение стационарного случайного процесса. Пусть X(t) - стационарный с.п., kX(τ) - его корреляционная функция, интегрируемая абсолютно на (-∞, +∞). Преобразование Фурье
называется спектральной плотностью с.п. X(t). Корреляционная функция kX(τ) выражается через спектральную плотность при помощи обратного преобразования Фурье
Соотношения (8) и (9) называется формулами Винера–Хинчина.
Свойства спектральной плотности стационарного с. п. 1) 2) 3) Из-за четности функций kX(τ) и SX(ω) формулы (8) и (9) можно представить в виде
Преобразование стационарного с.п. стационарной линейной динамической системой. Стационарная линейная динамическая система описывается линейным дифференциальным уравнением с постоянными коэффициентами
Введем обозначение
Обозначим
Функция Если на вход устойчивой стационарной линейной динамической системы (12) подается стационарный с.п. X(t), то в установившемся режиме на выходе будет стационарный с.п. Y(t). При этом верны следующие формулы.
1) 2) 3) 4)
РЕШЕНИЯ ЗАДАЧ 1. Найти математическое ожидание mX(t), корреляционную функцию КX(t1,t2), дисперсию DX(t) случайного процесса Х(t) = U sht – 3е-3t V + t2, где U, V - некоррелированные случайные величины, U Решение. Сначала вычислим м. о. и дисперсии случайных величин U и V: По свойству 2) п.2 м.о. от суммы с.п. равно сумме м.о. от слагаемых:
По свойству 1) п.2 м.о. неслучайной функции равно самой функции. Поэтому
В итоге получим
Теперь найдем корреляционную функцию. По свойству 3) п. 4 прибавление к с.п. неслучайной функции t2 не влияет на корреляционную функцию. Поэтому
Так как с.п. U sht и –3е-3t V некоррелированы из-за некоррелированности случайных величин U, V, то по формуле (2) получаем
Теперь по свойству 4) и 5) пункта 4 имеем
Таким образом,
Дисперсию найдем по свойству 6) пункта 4:
2. Найти корреляционную функцию КZ (t1,t2) и дисперсию DZ (t), если X(t), Y(t) – некоррелированные с.п., Z(t) = t2X(t) - Y(t) sin2t+ cost, и даны корреляционные функции КX (t1,t2) = 1+cos(t2–t1), КY (t1,t2) = exp(–|t2–t1|). Решение. По свойству 3) п.4 прибавление к с.п. неслучайной функции cost не влияет на корреляционную функцию. Далее, из-за некоррелированности с.п. t2X(t) и -Y(t) sin2t по формуле (2) имеем
Теперь по свойству 4) п.4 получаем
Дисперсию найдем по свойству 6) п.4 :
3. X(t), Y(t) – центрированные с. п., KX(t1, t2) = 4sint1sint2, KY(t1, t2) = 81sint1sint2, KX,Y (t1, t2) = 18sint1sint2. Найти математическое ожидание mZ (t), корреляционную функцию KZ (t1, t2), дисперсию DZ (t), нормированную корреляционную функцию ρZ (t1, t2) случайного процесса Z(t) = sin4t + e– 2 t X(t) - e–tY(t). Решение. Так как X(t), Y(t) – центрированные с. п., то их математические ожидания равны нулю. По свойствам 1), 2), 5) п.2 получаем
По свойству 3) п.4 прибавление неслучайной функции
По свойству 4) п.4 получаем
По свойству 4) п. 5 получаем
В итоге имеем
Дисперсию найдем по свойству 6) п.4:
По определению нормированной корреляционной функции (п. 4)
При этом ρZ (t1,t2) =1, если
4. Х(t) = ch2t – U sh2t, случайная величина U Решение. Найдем математическое ожидание и дисперсию случайной величины U: Найдем математическое ожидание с.п. X(t)
Найдем корреляционную функцию с.п. X(t)
Найдем дисперсию с.п. X(t ) по свойству 6) п. 4:
По свойству 1) из п.6 получаем
По свойству 2) из п.6 получаем
Дисперсию найдем по свойству 6) п.4
Найдем нормированную корреляционную функцию
Найдем взаимную корреляционную функцию KX,Y (t1, t2) по свойству 3) п.6:
Найдем нормированную взаимную корреляционную функцию:
5. X(t) = t+1+ t2U - V cos2t,где U Решение. Сначала найдем м. о. и дисперсии случайных величин U, V:
Найдем математическое ожидание с. п. X(t)
Найдем корреляционную функцию с.п. X(t) по формуле (2)
Найдем математическое ожидание производной с. п. X(t)
Найдем корреляционную функцию производной с. п. X(t)
Найдем взаимные корреляционные функции с. п. X(t) и его производной:
Найдем математическое ожидание с. п. Y(t)
Найдем корреляционную функцию с. п. Y(t) по формуле (1)
Найдем дисперсию с. п. Y(t) по свойству 6) п. 4:
6. Дан с. п. X(t) = (t 2 +1)U, U Решение. Найдем математическое ожидание и дисперсию случайной величины U: Найдем математическое ожидание с. п. X(t)
Найдем корреляционную функцию с.п. X(t)
Найдем математическое ожидание с. п. Z(t) формуле 1) п. 7:
Найдем корреляционную функцию с. п. Z(t) по формуле 2) п. 7:
Найдем дисперсию с. п. Z(t) по свойству 6) п. 4:
Найдем взаимные корреляционные функции по формуле 3) п. 7:
7. Решение. Найдем дисперсию случайной величины U : Найдем корреляционную функцию с.п. X(t)
Найдем корреляционную функцию с. п. Z(t) по формуле 2) п. 7:
Найдем взаимные корреляционные функции с. п. X(t), Z(t) по формуле 3) п. 7:
Найдем корреляционную функцию с. п. Y(t) по формуле (1):
Найдем дисперсию с. п. Y(t) по свойству 6) пункта 4:
Найдем нормированную корреляционную функцию с. п. Y(t)
При этом знак
8. Доказать, что с. п.
стационарен в широком смысле. Проверить свойство эргодичности для м. о. и корреляционной функции. Решение.Найдем Проверим равенства (3) и (4) п. 8. Найдем математическое ожидание с. п. X(t): Найдем корреляционную функцию с.п. X(t):
Таким образом, Проверим свойство эргодичности относительно математического ожидания mX . Пусть x(t) = ucos7t - vsin7t - реализация с. п. X(t). Преобразуем ее по известной формуле где Проверим равенство (6) п. 9:
Следовательно, с. п. X(t) эргодичен относительно м. о. Проверим свойство эргодичности относительно корреляционной функции.
что не совладает с Таким образом, равенство (7) п. 9 выполняется не для всякой реализации x(t) с.п. X(t), следовательно, с. п. X(t) не является эргодическим относительно корреляционной функции.
9. Дана корреляционная функция kX (τ) = exp(-3|τ|)(1+sin3|τ|) стационарного случайного процесса X(t). Найти корреляционную функцию, дисперсию производной X ¢(t), взаимную корреляционную функцию kX,X ¢(τ). Решение. Пусть По свойству 7) п. 8 имеем
Так как функция В итоге имеем Дисперсию найдем по свойству 1) п. 8 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 -центрированный с.п.
-центрированный с.п. .
. .
.
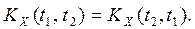
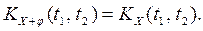
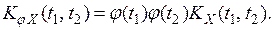
 .
.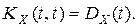
 .
. ,
,  .
. .
. .
. .
.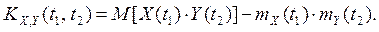
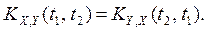
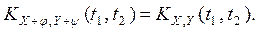

 .
. .
. , то
, то .
. попарно некоррелированы, то
попарно некоррелированы, то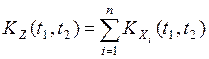 .
. и
и  теорема и следствие выглядят следующим образом.
теорема и следствие выглядят следующим образом. . (1)
. (1) и
и  некоррелированы, то
некоррелированы, то . (2)
. (2) - его производная. Тогда верны следующие свойства.
- его производная. Тогда верны следующие свойства. .
. .
. ,
,  .
. .
. .
. .
. ,
,  .
. .
. = const, (3)
= const, (3) , где
, где  . (4)
. (4) , где
, где  .
.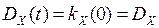 = const.
= const. .
.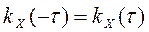 - четность функции.
- четность функции. , где
, где  - нормированная корреляционная функция с.п. X(t).
- нормированная корреляционная функция с.п. X(t). стационарный случайный процесс.
стационарный случайный процесс. .
. .
. ,
,  –
–  и
и  стационарно связаны
стационарно связаны . Тогда
. Тогда .
.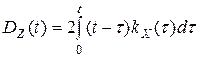 .
. ,
,  .
.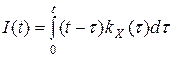 . Тогда по свойству 9) имеем
. Тогда по свойству 9) имеем . (5)
. (5) выполняется соотношение
выполняется соотношение  . Это можно доказать, сделав замену переменной t = –s в обоих интегралах I(–t) и
. Это можно доказать, сделав замену переменной t = –s в обоих интегралах I(–t) и  .
.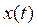
 . (6)
. (6) . (7)
. (7) (8)
(8) . (9)
. (9)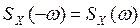 - четность спектральной плотности.
- четность спектральной плотности. .
. .
. (10)
(10) (11)
(11) . (12)
. (12) . Тогда уравнение (12) принимает вид
. Тогда уравнение (12) принимает вид .
.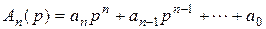 ,
,  .
. называется передаточной функцией стационарной линейной динамической системы (12). Функция
называется передаточной функцией стационарной линейной динамической системы (12). Функция  называется амплитудно-фазовой частотной характеристикой, а
называется амплитудно-фазовой частотной характеристикой, а  называется амплитудно-частотной характеристикой стационарной линейной динамической системы.
называется амплитудно-частотной характеристикой стационарной линейной динамической системы. .
. .
. .
.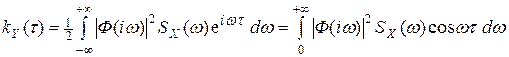 .
. R(-3; 3), V
R(-3; 3), V 

 .
. .
. . По свойству 5) п.2 множитель с. п. в виде неслучайной функции выносится за знак м.о. Следовательно,
. По свойству 5) п.2 множитель с. п. в виде неслучайной функции выносится за знак м.о. Следовательно,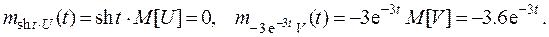

 .
. .
. ,
, 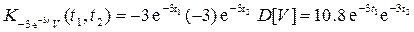 .
. .
. .
. .
.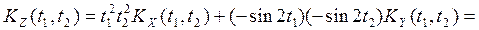
 .
. .
.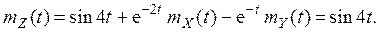
 к случайному процессу e– 2 t X(t) - e–tY(t) не меняет его корреляционной функции, то по формуле (1) получаем
к случайному процессу e– 2 t X(t) - e–tY(t) не меняет его корреляционной функции, то по формуле (1) получаем .
.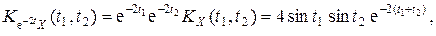
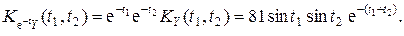
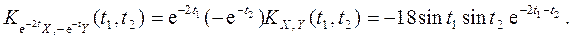
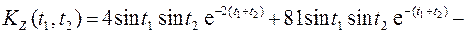
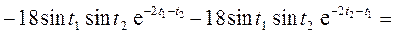
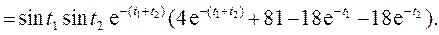
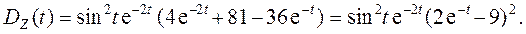
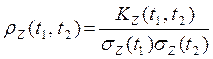 .
.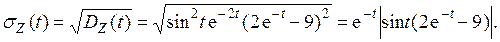
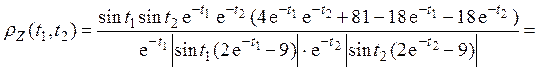
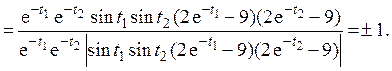
 , и ρZ (t1,t2) = -1, если
, и ρZ (t1,t2) = -1, если  .
. E(0.4), Y(t) = X¢(t). Найти математическое ожидание mY (t), корреляционную функцию KY (t1, t2), дисперсию DY (t), нормированную корреляционную функцию ρY (t1, t2) случайного процесса Y(t), не дифференцируя X(t). Найти взаимную корреляционную функцию KX,Y (t1, t2) и нормированную взаимную корреляционную функцию ρX,Y (t1, t2).
E(0.4), Y(t) = X¢(t). Найти математическое ожидание mY (t), корреляционную функцию KY (t1, t2), дисперсию DY (t), нормированную корреляционную функцию ρY (t1, t2) случайного процесса Y(t), не дифференцируя X(t). Найти взаимную корреляционную функцию KX,Y (t1, t2) и нормированную взаимную корреляционную функцию ρX,Y (t1, t2).
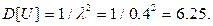
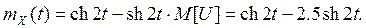
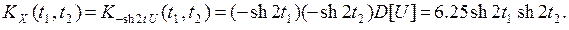
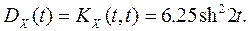
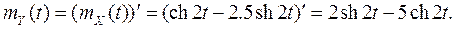
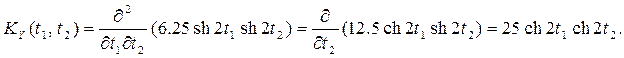
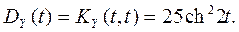
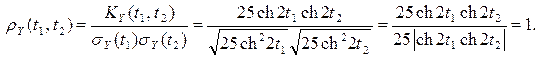
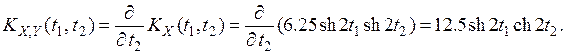
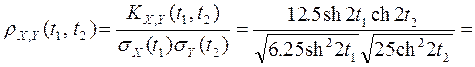
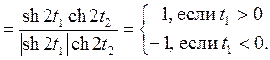
 В(10, 0.2) ,V
В(10, 0.2) ,V 
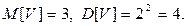
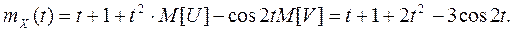
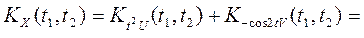
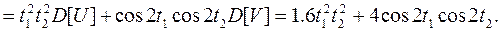
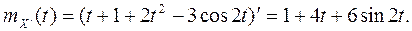
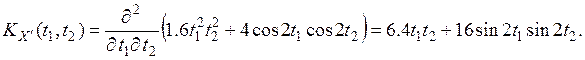
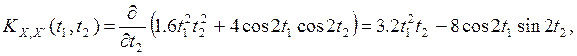
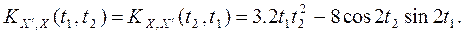
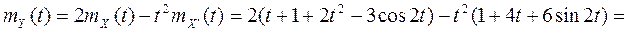
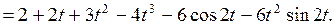
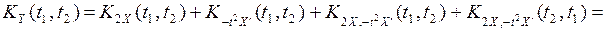
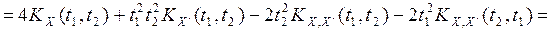
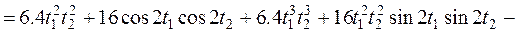

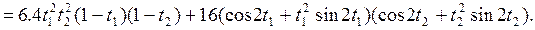

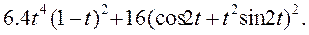
 Найти математическое ожидание mZ (t), корреляционную функцию КZ (t1,t2), дисперсию DZ (t), взаимные корреляционные функции KZ,X (t1,t2), KX,Z (t1,t2), не интегрируя X(t).
Найти математическое ожидание mZ (t), корреляционную функцию КZ (t1,t2), дисперсию DZ (t), взаимные корреляционные функции KZ,X (t1,t2), KX,Z (t1,t2), не интегрируя X(t).

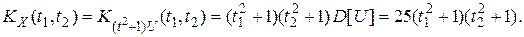
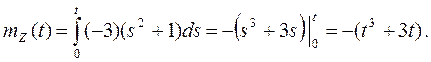

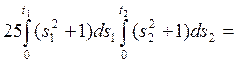
 .
.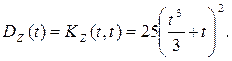
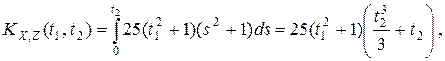
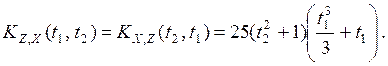
 Найти корреляционную функцию КY (t1,t2), дисперсию DY (t), нормированную корреляционную функцию ρY (t1,t2) случайного процесса Y(t)= X(t) + Z(t), не интегрируя X(t).
Найти корреляционную функцию КY (t1,t2), дисперсию DY (t), нормированную корреляционную функцию ρY (t1,t2) случайного процесса Y(t)= X(t) + Z(t), не интегрируя X(t).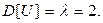
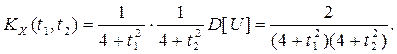
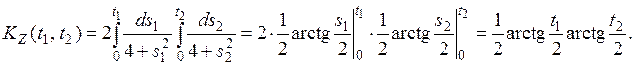
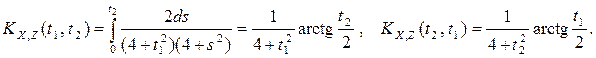
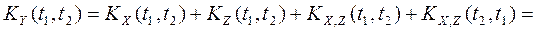
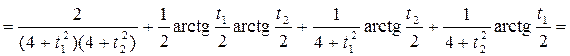


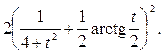
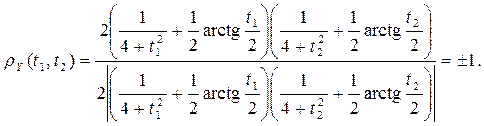
 совпадает со знаком выражения
совпадает со знаком выражения .
. , где
, где 
 ,
,

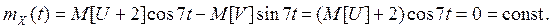
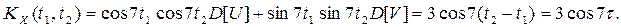
 , а корреляционная функция зависит только от t2 -t1, следовательно, с. п. X(t) стационарен ( в широком смысле).
, а корреляционная функция зависит только от t2 -t1, следовательно, с. п. X(t) стационарен ( в широком смысле). ,
, .
.
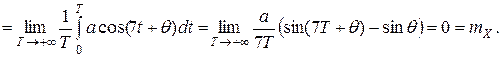

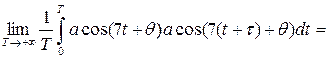
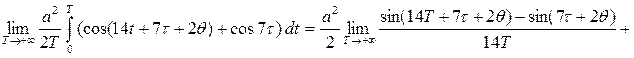
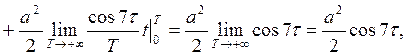
 при
при 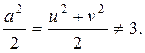
 . Тогда kX (τ) = exp(-3τ)(1+sin3τ).
. Тогда kX (τ) = exp(-3τ)(1+sin3τ).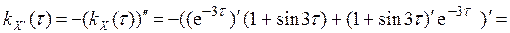
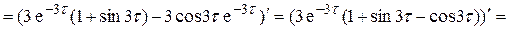
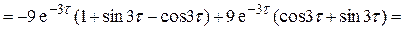

 – четная, то, доопределив полученную функцию по четности на интервале (-¥; 0), получим
– четная, то, доопределив полученную функцию по четности на интервале (-¥; 0), получим  .
.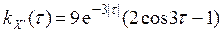 при tÎ (-¥; ¥)
при tÎ (-¥; ¥)