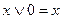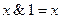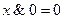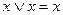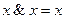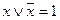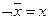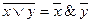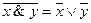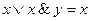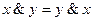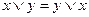|
|
Формулы логики высказываний12 Формула логики высказываний – это сложное высказывание, которое получено из простых высказываний, связанных между собой логическими операциями. С помощью введенных операций можно строить различные булевы функции. Порядок выполнения операций указывается скобками. Для упрощения принят ряд соглашений: 1. Действия в скобках; 2. Отрицание; 3. Конъюнкция; 4. Дизъюнкция; 5. Импликация; 6. Эквивалентность. Любая булева функция полностью определяется своей таблицей истинности. Пример 2. Определим таблицу истинности булевой функции Переменных: две (xи y), т.е. n = 2 Þ количество строк: 2n=22=4. с заголовком: 5 Количество столбцов: 2 переменные + 5 операций (&,, Порядок операций: 4 3 5 1 2
Искомая таблица истинности:
Задача 2. Определить значение истинности высказываний: а) 7 является простым числом, или 19 является простым числом. б) 2 + 3 = 6, и Архангельск расположен на Северной Двине. в) Если 12 делится на 6, то 12 делится на 4. г) 11 делится на 3 тогда и только тогда, когда 20 делится на 5. Решение: а) Данное высказывание является сложным, поэтому обозначим x - 7 является простым числом, a y - 19 является простым числом. Имеем, что x = 1, y = 1. Составим формулу x v y и, используя таблицу истинности, найдем логическое значение формулы. Получим x v y = 1. б) Данное высказывание является сложным, поэтому обозначим x - 2 + 3 = 6, а y - Архангельск расположен на Северной Двине. Имеем, что x = 0, y = 1. Составим формулу x Ù y и, используя таблицу истинности, найдем логическое значение формулы. Получим x Ù y = 0. в) Данное высказывание является сложным, поэтому обозначим x - 12 делится на 6, a y - 12 делится на 4. Имеем, что x = 1, y = 1. Составим формулу x ® y и, используя таблицу истинности, найдем логическое значение формулы. Получим x ® y = 1. г) Данное высказывание является сложным, поэтому обозначим x - 11 делится на 3, а y - 20 делится на 5. Имеем, что x = 0, y= I. Составим формулу x « y и, используя таблицу истинности, найдем логическое значение формулы. Получим x « y =0. Самостоятельно задача 3. Определите истинность составного высказывания:
А= {Принтер – устройство вывода информации}, B= {Процессор – устройство хранения информации}, C= {Монитор – устройство вывода информации}, D= {Клавиатура – устройство обработки информации}. Решение: сначала на основании знания устройств компьютера устанавливаем истинность простых высказываний: А=1, В=0, С=1, D=0. Определим теперь истинность составного высказывания, используя таблицы истинноcти логических операций: ( Составное высказывание ложно. Самостоятельно задача 4. Постройте таблицу истинности для функции F = x Ú y Ù z Переменных: три (x, y и z), т.е. n = 3 Þ количество строк: 2n=23=8. с заголовком: 9 Количество столбцов: 3 переменные + 3 операции (Ú,Ù,). итого 6 Порядок операций: 3 2 1 F = x Ú y Ù z
Задача 5. Даны значения: x = 0, y = 1, z = 1. Определите логические значения высказываний (x Ù y) « (z Ú y) (x Ù y) « (z Ú 1) (x Ù y) « (z Ú 0) (0 Ù 1) « (1 Ú 0) 0 « 1 0 (ложь) Тавтология и противоречие. Формула F(x1, x2, …, xn) называется тавтологией или тождественно истиной формулой, если при любых значения высказываний x1, x2, …, xn значение F=1. Формула F(x1, x2, …, xn) называется противоречием или тождественно ложной формулой, если при любых значения высказываний x1, x2, …, xn значение F=0. Задача 5. Определить, является ли формула тавтологией, противоречием или ни тем, ни другим: 1. x → (y → x); 2. x Ù ( (x Ú y).
Равносильные функции. Две функции называются равносильными, если они принимают одинаковые значения на любом наборе значений входящих в эти функции переменных, то есть у этих функций одинаковые таблицы истинности. Пример 3Используя таблицы истинности импликации и примера 2, получаем, что функции Пример 4. Являются ли формулы (x Ù y) и (x) Ú ( y) равносильными.
Задача 6Равносильны ли функции Основные равносильности: 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. Решение логических задач 
12 Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
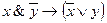
 ,Ú). итого 7
,Ú). итого 7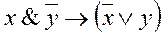



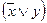


 &
&  ) & (C V D), состоящего из простых высказываний:
) & (C V D), состоящего из простых высказываний: &
&  ) & (1 V 0) = (0 & 1) & (1 V 0) = 0
) & (1 V 0) = (0 & 1) & (1 V 0) = 0 и
и  и
и