|
|
Основные логические операции12 Элементы алгебры логики. Использование логических законов при работе с информацией Математика является наукой, в которой все утверждения доказываются с помощью умозаключений, то есть путем законов человеческого мышления. Изучение законов человеческого мышления является предметом логики. Применение математики к логике позволило представить логические теории в новой удобной форме и применить вычислительный аппарат к решению задач, малодоступных человеческому мышлению, и это, конечно, расширило область логических исследований. Высказывания. Логика высказываний. Основным понятием математической логики является понятие «высказывания». Высказывание– это всякое повествовательное предложение, о котором можно однозначно сказать, что оно истинно или ложно. Пример 1. Высказывание «Пекин – столица летних Олимпийских игр 2008 года» истинно. Высказывание «21>23» ложно. Задача 1. Определить, какие из следующих предложений являются высказываниями: а) Студенты университета. б) 2 + 5 = 8. в) Сегодня плохая погода. г) Всякий человек имеет сестру. д) Для всех действительных чисел х и у верно равенство ху = ух. е) Треугольник ABC равен треугольнику А*В*С*. Решение: а) Предложение не является высказыванием, так как оно ничего не утверждает о студентах. б) Предложение является высказыванием, так как мы можем сказать, что оно ложно. в) Предложение не является высказыванием, так как мы не можем определить, истинно оно или ложно, потому что не знаем, где и когда это должно произойти. г) Предложение является высказыванием, так как оно принимает ложное значение. д) Предложение является высказыванием, так как оно принимает истинное значение. е) Предложение не является высказыванием, так как мы не можем определить, истинно оно или ложно, потому что не знаем, о каких именно треугольниках идет речь. Элементарное (простое) высказывание– это одно утверждение. Будем обозначать элементарные высказывания малыми буквами латинского алфавита x, y, z,…, истинное высказывание – цифрой 1, ложное высказывание – цифрой 0. Мы будем рассматривать функции на множестве переменных x и y. Переменные и функции могут принимать только значения 0 и 1. Это булевы функции. Высказывания, которые получаются из элементарных с помощью грамматических связок «не», «и», «или», «если .... , то ...», «тогда и только тогда», называются сложными или составными. Обозначаются F(x,y,z…) Также могут принимать значения «ИСТИНА» или «ЛОЖЬ» в зависимости от того, какие значения имеют входящие в их состав логические переменные и от действий над ними. Основные логические операции Значение функции можно задать с помощью таблицы истинности, которая показывает, чему равна функция на всех возможных комбинациях значений ее переменных. Отрицание Присоединение частицы «НЕ» к высказыванию называется операцией логического отрицания, или инверсией. Логическое отрицание (инверсия) делает истинное высказывание ложным, а ложное – истинным F(x) = x или F(x) = Таблица истинности этой функции имеет следующий вид:
Мы видим, что отрицание меняет возможные значения переменной на противоположные. Дизъюнкция Объединение двух или более высказываний в одно с помощью союза «ИЛИ» называется операцией логического сложения, или дизъюнкцией. Логическая функция, полученная в результате дизъюнкции, истинна тогда, когда истинна хотя бы одна из входящих в него логических переменных F(x, y) = x Ú y или F(x, y) = x + y или F(x, y) = x or y Таблица истинности этой функции имеет следующий вид:
Мы видим, что дизъюнкция равна 1, если хотя бы один из ее аргументов равен 1. Конъюнкция Объединение двух или более высказываний в одно с помощью союза «И» называется операцией логического умножения, или конъюнкцией Логическая функция, полученная в результате конъюнкции, истинна тогда и только тогда, когда истинны все входящие в него логические переменные. F(x, y) = x & y или F(x, y) = x Ù y или F(x, y) = x * y или F(x, y) = x and y Таблица истинности этой функции имеет следующий вид:
Мы видим, что конъюнкция равна 1 тогда и только тогда, когда оба ее аргумента равны 1. Импликация Объединение двух высказываний, из которых первое является условием, а второе – следствием из него, называется импликацией. Импликация ложна тогда и только тогда, когда условие истинно, а следствие ложно Пример: Если выучишь материал, то сдашь зачет Это высказывание ложно только тогда, когда материал выучен, а зачет не сдан, т.к. сдать зачет можно и случайно, например если попался единственный знакомый вопрос или удалось воспользоваться шпаргалкой Таблица истинности этой функции имеет следующий вид:
Импликация как булева функция ложна лишь тогда, когда посылка истинна, а следствие ложно. Эквиваленция ( или эквивалентность) x~y (x « y) (читается «x тогда и только тогда, когда y»). Эквивалентность – это логическая операция, объединяющая два простых высказывания в одно составное и которое является истинным Таблица истинности этой функции имеет следующий вид: 
12 Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
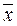( читается «не x»).
или F(x) = not x
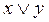(читается «x или y»).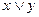
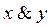(читается «x и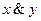 y»)..
(читается «если x, то y»).