
|
|
Распределение мощности нагрузки между параллельно работающими агрегатами электрических станцийРасходные характеристики агрегатов (зависимость затрат на производство электрической энергии как функции мощности генерирующего агрегата) существенно различаются в зависимости от типа агрегата, времени его изготовления, вида и типа используемого топлива и др. Поскольку суммарная мощность агрегатов, как правило, больше мощности нагрузки, то появляется возможность перераспределить нагрузку между агрегатами, загружая при этом более экономичные. Однако что такое "более экономичные"? Можно подумать, что это те, которые имеют меньшие удельные издержки (себестоимость производства электроэнергии). Однако при оптимальном распределении нагрузки агрегаты загружаются не в порядке увеличения себестоимости. Рассмотрим задачу оптимального распределения нагрузки в математической постановке. В качестве критерия оптимальности логично принять минимум суммарных затрат на топливо. Отсюда поставленная задача формулируется следующим образом. Требуется определить мощность Pi генераторов, реализующих минимум суммарных затрат на топливо:
при условии
где сi - цена топлива на станции; Вi(Рi) - расходная характеристика блока i; Рн - мощность нагрузки ЭЭС, которая в данной задаче считается постоянной величиной; π - потери мощности в ЭЭС, в общем случае, безусловно, зависящие от Рi. Задачи подобного типа решаются методами нелинейного программирования. Аналитическое решение можно получить, если пренебречь условиями - неравенствами (9.10). В этом случае решение может быть найдено методом Лагранжа, согласно которому отыскивается минимум функции Лагранжа:
где λ - неопределенный множитель Лагранжа. Выражение (9.11) можно представить в виде L(Р1,Р2,...,Рn)= ∑сiВi(Рi)+ λ(∑Рi - Рн- π) Решение задачи определяется приравниванием к нулю частных производных от функции Лагранжа:
где Выражая λ из (9.12), легко получаем условие оптимального распределения нагрузки:
Если считать потери мощности неизменными, π = const;. а топливо однотипным, то условие (9.14) преобразуется к виду:
Таким образом, для оптимального распределения нагрузки необходимо равенство относительных приростов (ОП) затрат на топливо. В первую очередь экономически выгодно загружать те агрегаты, которые имеют меньший относительный прирост, а не меньшие удельные затраты, как можно было бы ожидать. Это следует даже из простых рассуждений. Относительный прирост определяет приращение расхода топлива на каждый МВт прироста мощности. Отсюда, безусловно, в первую очередь необходимо загружать тот агрегат, который обеспечивает наименьший прирост затрат, т.е. имеющий наименьший относительный прирост. Критерий равенства ОП можно реализовать путем использования табличного метода. Каждая ХОП представляется в виде обратной функции Р(ε). Относительный прирост записывается строкой с заданной дискретностью, например, Δε =0,05 (табл. 9.1). Ниже записываются соответствующие значения мощностей каждого блока (в таблице второму блоку мощности 160 МВт соответствует ОП, равный 0,45). Исходя из критерия равенства ОП, можно составить ХОП системы в целом путем суммирования мощностей. Распределение любой нагрузки Рн (с учетом потерь мощности) между блоками можно выполнить путем определения ОП, соответствующего Рс=Рн (выбор строки) и определения всех мощностей блоков, записанных в данной строке. Например, если Рс=Рн=250 МВт, то Р1=70 МВт, а Р2=180 МВт (все величины соответствуют ε = 0,5). В случае необходимости можно применить линейную аппроксимацию. Таблица 9.1
Примеры. I. Определить оптимальное распределение нагрузки Рн = 400 МВт между параллельно работающими агрегатами с заданными расходными характеристиками: В1(Р1) = 0,02 В2(Р2) = 0,01 Решение. Распределение нагрузки выполняется по критерию равенства относительных приростов. В простых случаях (два агрегата) оказывается возможным решить заданную задачу путем непосредственного дифференцирования расходных характеристик с последующим приравниванием ХОП. Характеристики относительных приростов агрегатов: ε1 (Р1) = 0,04·Р1, + 0,2 ; ε2 (Р2) = 0,02·Р2 + 0,1. Система уравнении для определения Р1,Р2: 0,04·Р1 + 0,2 = 0,02·Р2 + 0,1 ; Р1 + Р2 = 400. Отсюда Р1 =132 МВт, Р2 = 268 МВт (соответствуют ограничениям). Замечание. Если 200 ≤ Р1 ≤300 МВт, 100≤ Р2 ≤ 200 МВт, то полученное решение не удовлетворяет системе ограничений. В этом случае следует выполнить коррекцию решения: Р1 = 200 МВт (минимум), Р2 = 200 МВт (остаток). 2. Определить оптимальное распределение нагрузки Рн = 180 МВт между параллельно работающими агрегатами с линейными расходными характеристиками (нереальная ситуация): В1 (Р1) = 0,35·Р1+ 250, 100 ≤ Р1 ≤300 МВт. В2(Р2) = 0,3·Р2+300, 50 ≤ Р2 ≤200 МВт. Решение. Характеристики относительных приростов в данном примере не зависят от мощности: ε1 (Р1) = 0,35; ε2 (Р2) = 0,З. Равенство относительных приростов невозможно. Здесь в первую очередь загружается до максимума второй агрегат с меньшим относительным приростом. При этом необходимо учитывать ограничение на минимальную мощность первого агрегата. Окончательное решение: Р1 =100 МВт (минимум), Р2 = 80 МВт. 9.3. Изменение роли переменных x и u в функции Лагранжа Для практического использования метода Лагранжа следуют отметить некоторую специфику представления функции Лагранжа в различных задачах оптимизации. В качестве основной принимается форма (9.6) для функционала (9.4) при условии (9.5)
где Аналогичную структуру имеет функция Лагранжа в случае, когда 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
 - так называемая характеристика относительных приростов (ХОП) агрегата, определяемая путем дифференцирования расходной характеристики
- так называемая характеристика относительных приростов (ХОП) агрегата, определяемая путем дифференцирования расходной характеристики  ;
;  - частная производная потерь мощности в ЭЭС по мощности агрегата i, имеющая сложную функциональную зависимость. Здесь мы будем считать ее постоянной заданной величиной.
- частная производная потерь мощности в ЭЭС по мощности агрегата i, имеющая сложную функциональную зависимость. Здесь мы будем считать ее постоянной заданной величиной.
 .
.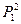 + 0,2
+ 0,2  + 250, 100 <= Р1 <=200 МВт.
+ 250, 100 <= Р1 <=200 МВт. + 0,1 Р2· + 300, 200 <= Р2 <=300 МВт.
+ 0,1 Р2· + 300, 200 <= Р2 <=300 МВт.
 -вектор множителей Лагранжа
-вектор множителей Лагранжа . Остальные формы следуют из (9.15) исходя из соотношений
. Остальные формы следуют из (9.15) исходя из соотношений  ,
,  . При этом следует помнить, что если
. При этом следует помнить, что если  -любое, то
-любое, то  , и наоборот если
, и наоборот если  .
.