
|
|
Произвольная плоская система сил
Под произвольной системой сил понимают совокупность сил, расположенных в одной плоскости, линии действия которых не пересекаются в одной точке. Произвольную плоскую систему сил можно значительно упростить, приведя силы к одному центру приведения О. В результате чего в этом центре будет приложена сила Главный вектор
Численное значение главного вектора определяется по его проекциям на координатные оси:
где
Направление главного вектора находят по косинусам направляющих углов:
где Условиями равновесия тела под действием произвольной плоской системы сил являются равенство нулю главного вектора и главного момента относительно любого центра О:
Эти условия выполняются, если
Уравнения (1) называются основными уравнениями равновесия. Существуют еще две формы уравнений равновесия:
В системе уравнений (2) ось х не должна быть перпендикулярной к прямой, проходящей через центры А и В, а центры А, В и С в системе (3) не должны лежать на одной прямой.
Пример С1. Жесткая рама АDСВ (рис. С1) имеет в точке А неподвижную шарнирную опору, а в точке В – подвижную шарнирную опору на катках. Все действующие нагрузки и размеры показаны на рисунке. Дано: F = 25 кН, a = 60°, Р = 18 кН, g = 75°, М = 50 кН×м, b = 30°, а = 0,5 м. Определить: реакции в точках А и В, вызываемые действующими нагрузками. Решение. 1. Рассмотрим равновесие рамы. Проведем координатные оси ху и изобразим действующие на раму силы: силу
Рис. С1
2. Для полученной плоской системы сил составим три уравнения равновесия. При вычислении момента силы
Из уравнения (6) находим:
Из уравнения (4):
Из уравнения (5):
Ответ:
Знаки указывают, что реакции Для проверки правильности полученных результатов составим и решим проверочное уравнение равновесия в форме моментов всех сил относительно точки С.
Пример С2. Конструкция состоит из жесткого угольника АЕС и стержня СК, которые в точке С (рис. С2а) соединены друг с другом с помощью цилиндрического шарнира. Внешними связями являются: в точке А - шарнирно-неподвижная опора, в точке В - невесомый стержень ВВ¢, в точке D - шарнирно-подвижная опора. К конструкции приложена сила Дано: F = 10 кН, a = 60°, q = 20 кН/м, М = 50 кН×м, а = 0,5 м. Определить реакции связей в точках А, В, С и D, вызванные заданными нагрузками.
Рис. С2а
Решение.1. Для определения реакций расчленим систему по шарниру С и рассмотрим сначала равновесие стержня КС (рис. С2б). Проведем координатные оси ху и изобразим действующие на стержень силы: равномерно распределенную нагрузку заменим силой
Рис. С2б Для полученной плоской системы сил составляем три уравнения равновесия:
При вычислении момента силы Из уравнения (9) находим:
Из уравнения (7):
Из уравнения (8):
2. Теперь рассмотрим равновесие угольника (рис. С2в).
Рис. С2в На него действуют: сила
В уравнении (12) при вычислении момента силы Из уравнения (12) находим:
Из уравнения (10):
Из уравнения (11):
Ответ: RAx = - 3,08 кH, RAу = 18,685 кH, RD = 6,645 кH, RB = 30,8 кH, RCx = 1,92 кH, RCy = 16,67 кH. Знаки указывают, что сила реакции Система сходящихся сил Пример С3. . Конструкция состоит из невесомых стержней 1, 2, ..., 6, соединенных друг с другом (в узлах K и М) и с неподвижными опорами А, В, С, D шарнирами (рис. С3). В узлах K и М приложены силы Дано: Р = 100 Н, a1 = 60°, b1 = 60°, g1 = 45°; Q = 50 H, a2 = 45°, b2 = 60°, g2 = 60°, y = 30°, j = 60°, d = 74°. Определить усилия в стержнях 1-6.
Рис. С3
Решение. 1. Рассмотрим равновесие узла K, в котором сходятся стержни 1, 2, 3. На узел действуют сила
Из уравнения (15) находим:
Из уравнения (13):
Из уравнения (14):
N1 = P×cos b1 - N2×cos y.
N1 = 100×cos 60° - (-345)×cos 30° = 348,78 Н.
2. Рассмотрим равновесие узла М. На узел действуют сила
При определении проекций силы Решая уравнение (17), находим:
Из уравнения (16):
Из уравнения (18):
Ответ: N1 = 348,78 H, N2 = - 345 H, N3 = 141 H, N4 = 49,79 H, N5 = 328,86 H, N6 = 65,48 H. Знаки показывают, что стержень 2 сжат, остальные растянуты.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 , называемая главным вектором, и к телу в целом будет приложена пара сил с моментом МО, называемым главным моментом относительно этого центра.
, называемая главным вектором, и к телу в целом будет приложена пара сил с моментом МО, называемым главным моментом относительно этого центра. ,
, 
 ,
, и
и 


 ,
,  - орты осей Ох и Оу.
- орты осей Ох и Оу. (1)
(1) (2)
(2) (3)
(3) , пару сил с моментом М, натяжение троса
, пару сил с моментом М, натяжение троса  (по модулю Т = Р) и реакции связей
(по модулю Т = Р) и реакции связей  ,
,  ,
,  (реакцию неподвижной шарнирной опоры А изображаем двумя ее составляющими, реакция шарнирной опоры на катках направлена перпендикулярно опорной плоскости).
(реакцию неподвижной шарнирной опоры А изображаем двумя ее составляющими, реакция шарнирной опоры на катках направлена перпендикулярно опорной плоскости).
 ,
,  (
( 
 ) и учтем, что
) и учтем, что 
 . Получим:
. Получим: (4)
(4) (5)
(5) (6)
(6)








 и
и  направлены противоположно показанным на рисунке.
направлены противоположно показанным на рисунке.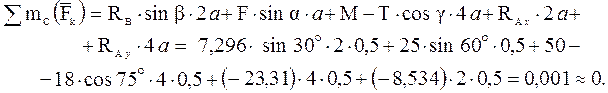
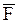 , пара сил с моментом М и равномерно распределенная на участке КВ нагрузка интенсивности q.
, пара сил с моментом М и равномерно распределенная на участке КВ нагрузка интенсивности q.
 , приложенной в середине участка ВК (численно Q = q×2а = 20 кН), реакцию
, приложенной в середине участка ВК (численно Q = q×2а = 20 кН), реакцию 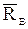 стержня ВВ¢ направим вдоль этого стержня, а действие отброшенного угольника АЕС представим составляющими
стержня ВВ¢ направим вдоль этого стержня, а действие отброшенного угольника АЕС представим составляющими  и
и  реакции шарнира С.
реакции шарнира С.
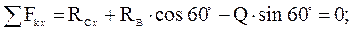 (7)
(7) (8)
(8) (9)
(9) и
и  и применяем теорему Вариньона (
и применяем теорему Вариньона (  ,
,  ).
).




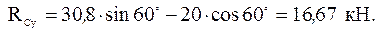

 шарнирно-подвижной опоры D, составляющие
шарнирно-подвижной опоры D, составляющие  и
и  реакции шарнирно неподвижной опоры А и составляющие
реакции шарнирно неподвижной опоры А и составляющие  и
и  реакции
реакции  , направленные противоположно соответствующим реакциям
, направленные противоположно соответствующим реакциям  и
и  =
=  и
и  =
=  , в силу равенства действия и противодействия. Для этой плоской системы сил тоже составляем три уравнения равновесия:
, в силу равенства действия и противодействия. Для этой плоской системы сил тоже составляем три уравнения равновесия: (10)
(10) (11)
(11) (12)
(12) ) и применена теорема Вариньона.
) и применена теорема Вариньона.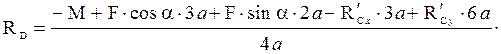





 направлена противоположно показанной на рис. С2в.
направлена противоположно показанной на рис. С2в. и
и 
 ,
,  ,
,  стержней, которые направим по стержням от узла, считая стержни растянутыми. Составим уравнения равновесия этой пространственной системы сходящихся сил:
стержней, которые направим по стержням от узла, считая стержни растянутыми. Составим уравнения равновесия этой пространственной системы сходящихся сил: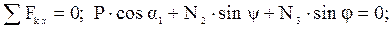 (13)
(13) (14)
(14) (15)
(15)


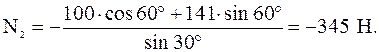
 ,
,  ,
,  ,
,  стержней. При этом по закону о равенстве действия и противодействия реакция
стержней. При этом по закону о равенстве действия и противодействия реакция  , численно же
, численно же  = N2. Составим уравнения равновесия:
= N2. Составим уравнения равновесия: (16)
(16)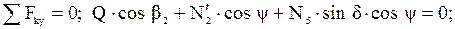 (17)
(17) (18)
(18) этой силы на плоскость хОу (по числовой величине
этой силы на плоскость хОу (по числовой величине  ), а затем найденную проекцию на плоскость спроектировать на оси х, у.
), а затем найденную проекцию на плоскость спроектировать на оси х, у.




