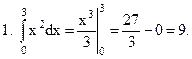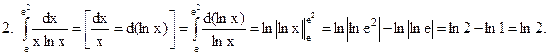|
|
Вопрос 3. Определенный интеграл как функция верхнего предела12 ОСНОВНАЯ ФОРМУЛА ИНТЕГРАЛЬНОГО ИСЧИСЛЕНИЯ
На сегодняшней лекции мы продолжим изучение определенного интеграла и получим формулу для его вычисления. Как мы увидим позже, определенный интеграл равен приращению первообразной, и представляет собой постоянное число, равное площади криволинейной трапеции. Поэтому все методы вычисления неопределенного интеграла справедливы и для определенного интеграла.
Вопрос 1. Основные свойства определенного интеграла Интеграл
был введен для случая a < b. Обобщим понятие определенного интеграла на случай, когда пределы интегрирования совпадают или нижний предел больше верхнего. Свойство 1. Эта формула получается из (1) при условии, что все Δxi = 0.
Свойство 2. Эта формула получается из (1) при условии, что отрезок [a;b] пробегается в обратном направлении (от b к а), т.е. все Δxi < 0.
Свойство 3. (свойство аддитивности) Если функция f(x) интегрируема на отрезке [a;b] и a < c < b, то
Равенство (2) справедливо при любом расположении точек а, b и с (считаем, что функция f(x) интегрируема на большем из получающихся отрезков).
Свойство 4. Постоянный множитель можно выносить за знак определенного интеграла, т.е.
где k = const. Свойство 5. Определенный интеграл от алгебраической суммы двух функций равен алгебраической сумме интегралов этих функций, т.е.
Замечание
Вопрос 2. Оценки интеграла. Теорема о среднем Будем считать, что всюду a < b. 1. Если всюду на отрезке [a;b] функция f(x) ≥ 0, то 2. Если всюду на отрезке [a;b] f(x) ≥ g(x), то 3. Для функции f(x), определенной на отрезке [a;b], имеет место неравенство В частности, если всюду на отрезке [a;b] 4.Если m и М – соответственно наименьшее и наибольшее значения функции f(x) на отрезке [a;b], то Т.2.1. (теорема о среднем) Если функция f(x) непрерывна на отрезке [a;b], то на этом отрезке существует точка с, такая, что
Равенство (3) называется формулой среднего значения, а величина f(c) - называется средним значением функции f(x) на отрезке [a;b]. Вопрос 3. Определенный интеграл как функция верхнего предела
Если функция y = f(x) интегрируема на отрезке [a;b], то она интегрируема и на любом меньшем отрезке, т.е. для "xÎ[a;b] существует интеграл
Для того чтобы не смешивать обозначения предела и переменной интегрирования, обозначим переменную интегрирования через t. Тогда интеграл (4) запишется в виде
Функция Ф(х) называется интегралом с переменным верхним пределом.
Рассмотрим некоторые свойства функции Ф(х).
Т.3.1.(непрерывность функции Ф(х)) Если функция f(x) непрерывна на отрезке [a;b], то функция Ф(x) будет так же непрерывна на отрезке [a;b].
Т.3.2.(дифференцирование функции Ф(х)) Если функция f(x) непрерывна на отрезке [a;b], то функция Ф(x) дифференцируема в любой внутренней точке х этого отрезка, причем справедливо равенство
Следствие Если функция f(x) непрерывна на отрезке [a;b], то для этой функции существует первообразная на данном отрезке, причем функция Ф(x) - интеграл с переменным верхним пределом – является первообразной для функции f(x).
Так как всякая другая первообразная для функции f(x) отличается от Ф(x) только на постоянное слагаемое, то можно установить связь между неопределенным и определенным интегралами:
где С – произвольная постоянная. Вопрос 4. Вычисление определенного интеграла. Формула Ньютона-Лейбница Вычисление определенных интегралов методом, основанным на определении интеграла как предела интегральных сумм, как правило, связано с большими трудностями. Существует более удобный метод вычисления определенных интегралов, который основан на установленной связи между неопределенным и определенным интегралами.
Т.4.1. Если функция f(x) непрерывна на отрезке [a;b] и F(x) - любая первообразная для функции f(x) на [a;b], то справедлива формула
Формула (6) называется формулой Ньютона – Лейбница.
Если ввести обозначение
Формула Ньютона – Лейбница дает удобный способ вычисления определенных интегралов. Чтобы вычислить определенный интеграл Пример

12 Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
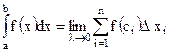 (1)
(1) .
.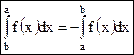 .
.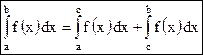 . (2)
. (2) ,
,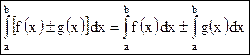 .
.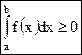 .
. .
. .
.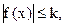 то
то  и
и 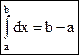 .
.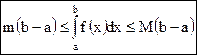 .
.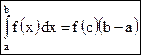 . (3)
. (3)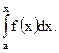 (4)
(4)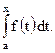 Величина этого интеграла является функцией верхнего предела х и обозначается Ф(х):
Величина этого интеграла является функцией верхнего предела х и обозначается Ф(х):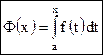 . (5)
. (5)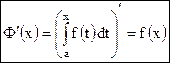 .
.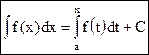 ,
,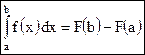 . (6)
. (6)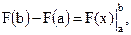 то формулу Ньютона-Лейбница (6) можно переписать в виде
то формулу Ньютона-Лейбница (6) можно переписать в виде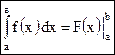 .
.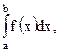 необходимо найти любую первообразную функцию F(x) для f(x) и взять разность F(b) ‒ F(a) на концах отрезка [a;b].
необходимо найти любую первообразную функцию F(x) для f(x) и взять разность F(b) ‒ F(a) на концах отрезка [a;b].