
|
|
Задача о кратчайших путях между всеми парами узлов.В предыдущих параграфах этой главы рассматривались задачи нахождения оптимальных в том или ином смысле путей от некоторого фиксированного узла до всех остальных узлов сети. Здесь мы рассмотрим задачу построения кратчайших путей между всеми парами узлов. Под длиной пути, также как и ранее в параграфах 1-3, понимаем сумму весов дуг, образующих этот путь. Ясно, что эту задачу можно решать, используя n раз (поочередно для каждого узла) один из описанных ранее алгоритмов нахождения расстояний от фиксированного узла. Таким образом, мы получаем алгоритмы сложности O(n4) (при использовании алгоритма Форда-Беллмана) и O(n3) для сетей с неотрицательными весами (алгоритм Дейкстры) или для бесконтурных сетей (алгоритм 6.6). Однако, для общего случая сетей с произвольными весами имеются более эффективные алгоритмы, чем метод, основанный на п-кратном применении алгоритма Форда-Беллмана. Один из таких алгоритмов, предложенный в 1962 году Флойдом, мы здесь и разберем. Пусть сеть G=(V,E,c) задана матрицей весов А, где А| i,j | c(vi,vj), и A[i,j]=+∞, если дуги (vi,vj) в сети нет. Обозначим через dk(i,j) длину кратчайшего пути из vi и vj, все промежуточные узлы которого содержатся в множестве {v1,...,vk}, то есть содержатся в первых к узлах. Будем считать, что d1(i,j)=A[i,j]. Пусть dk(i,j) вычислено для всех i,j=l,...,n, и некотором k≥1. Докажем равенство dk+1(i,j) = min(dk(i,j), dk(i,k+l) + dk(k+l, j)). (6.5) Действительно, рассмотрим кратчайший vi-vj-путь р с промежуточными узлами из множества {v1,…,vk,vk+1}. Возможны две ситуации: либо узел vk+1 входит в этот путь, либо нет. Если узел vk+1 не входит в путь р, то, как легко видеть, справедливо равенство dk+1(i,j)= dk(i,j). Если же узел vk+1 входит в путь р, то разбивая это путь на пути от v, до vk+1 и от vk+1 до vj, получаем два новых пути, все промежуточные узлы которых входят во множество {v1,...,vk}. Поскольку всякий подпуть кратчайшего пути сам является кратчайшим путем между соответствующими узлами, то справедливо равенство dk+1(i,j) = dk(i,k+l) + dk(k+l,j)), что завершает обоснование равенства (6.5). Равенство (6.5) позволяет легко вычислять расстояния между всеми парами узлов, последовательно вычисляя для всех пар узлов значения d1(i,j). d2(i,j),..., dn(i,j), так как расстояние от v1 до vj равно dn(i,j). Для нахождения самих кратчайших путей будем использовать аналог неоднократно применявшегося ранее массива ОТЕЦ, а именно, заведем матрицу ПРЕД размера n Детали изложены в алгоритме 6.9, где предполагается, что A[i,i]=0, A[i,j]=+∞, если (vi,vj)
АЛГОРИТМ 6.10 ФЛОЙД (* Вычисление расстояний между всеми парами узлов *) Данные: Сеть G=(V,E,c), заданная матрицей весов А[...n, 1...n]. Результаты: Расстояния D[i,j] для всех пар vi, vj
Понятно, что сложность алгоритма 6.10 определяется сложностью цикла в строках 5-9, который состоит из трех вложенных циклов, выполняемых n раз каждый. Отсюда следует
Теорема 6.7. Алгоритм Флойда имеет сложность O(n3). Здесь интересно отметить, что точно такую же сложность имеет алгоритм Форда-Беллмана вычисления расстояний от фиксированного узла до всех остальных узлов сети. В настоящее время не известен ни один алгоритм вычисления расстояния между фиксированной парой узлов, который был бы существенно эффективнее (то есть имел бы меньшую вычислительную сложность), чем алгоритм вычисления расстояний между всеми парами узлов. Впрочем, неизвестно также существует или нет такой алгоритм. Формальное описание процедуры построения самих кратчайших путей, использующее в качестве исходных данных матрицу ПРЕД, не составляет никаких трудностей, и мы предоставляем его читателям в качестве несложного упражнения для самостоятельной работы.
Результаты работы цикла в строках 2-6: D= Результаты работы цикла в строках 7-13 при k=1 D= Результаты работы цикла в строках 7-13 при k=2 D= Результаты работы цикла в строках 7-13 при k=3 D= Нетрудно проверить, что обе эти матрицы останутся неизменными в результате работы цикла 7-13 при k = 4. Вот кратчайшие пути для некоторых пар узлов: 2-4: 2-3-1-4; 1-3: 1-2-3; 3-2: 3-1-2.
ЗАДАЧИ 1.Пути в орграфе с взвешенными узлами. Пусть G=(V,E) — орграф с заданной функцией весов узлов: d: V -» R. Для s-t-пути р: v0=s,vi,...,vk=t в орграфе G, положим d(p)=∑{d(vr): r=l,2,...k}. Свести задачу о построении s-t-пути р в G с минимальным значением d(p) к задаче о построении кратчайшего пути между s и t в подходяще построенной сети. 2.Пути в сетях с взвешенными узлами. Пусть G=(V,E,c) — сеть с заданной функцией весов узлов d: V→R. Для s-t-пути р: v0=s,v1,...,vk=t в сети G положим f(p)= ∑{c(vr-1,vr) + d(vr)}. Свести задачу о построении s-t-пути в G с минимальным значением f(p) к задаче о построении кратчайшего пути в подходяще построенной сети. 3.Пути между фиксированными множествами узлов. Пусть в сети G=(V,E,c) зафиксировано два множества узлов S и T, S 4.Напишите алгоритм сложности О(m), осуществляющий топологическую сортировку узлов бесконтурного орграфа, заданного списками СЛЕД. Указание: докажите, что каждый такой орграф содержит хотя бы один узел, степень захода которого равна нулю. Начните нумерацию по возрастанию номеров со всех таких узлов, удаляя каждый раз пронумерованный узел вместе со теми дугами, из него выходящими. Предложите алгоритм сложности О(n2), осуществляющий топологическую сортировку узлов беcконтурного орграфа, заданного матрицей смежности. 5.Напишите алгоритм сложности О(m), вычисляющий расстояния от v до всех остальных узлов в бесконтурной топологически отсортированной сети, заданной списками смежностей СЛЕД, и алгоритм сложности O(n2) для сети, заданной матрицей несом. 6.Промышленная компания планирует начать производство кондиционеров, состоящих из трех основных частей: корпуса, вентилятора и мотора. Затраты на оборудование предприятия станками, производящими корпуса, вентиляторы и моторы, составляют 20000, 50000 и 80000 руб. соответственно. Если вначале наладить выпуск вентиляторов, то затраты на оборудование предприятия станками, производящими корпуса и моторы, будут уменьшены на 5%. Если вначале пустить в производство моторы, то затраты на оснащение предприятия станками двух других типов уменьшатся на 10%. Если же в первую очередь будет налажен выпуск корпусов, то остальные затраты уменьшатся на 5%. После того, как будет налажен выпуск двух компонентов, затраты на производство третьего компонента дополнительно уменьшатся на 5% Как организовать производство с наименьшими затратами? 7.Промышленной компании нужно составить план замены оборудования на ближайшие 4 года. На данный период ожидаются следующие расходы и амортизационные стоимости. Существующая цена станка составляет 20000 ед. Ожидается ежегодное увеличение цен па станки на 10%. В первые два года станки изнашиваются на 25%, а в последующие два года — на 15%. Издержки на техническое обслуживание и текущий ремонт в ближайшие 4 года составят 1200, 1500, 1900 и 2400 ед. соответственно. Станки можно заменять каждый год или каждые 2, 3 и 4 года. Составить план замены оборудования, при котором общие издержки на ближайшие 4 года были бы минимальными. 8.Крупную партию груза требуется доставить из пункта А в пункт В. Вывезти груз из А можно двумя способами: либо грузовыми самолетами до пункта С, либо морским путем до порта D. Из пункта С до В груз можно доставить автотранспортом, стоимость перегрузки 1 тонны с самолетов в автомобили составляет 0,4 ед. Из порта D продукция может быть либо доставлена в пункт В по железной дороге, в этом случае стоимость перегрузки 1 тонны с морских барж в железнодорожные вагоны составляет 0,2 ед., либо транзитом через пункт С доставлена автотранспортом. при этом стоимость перегрузки с морских барж в автомобили составляет 0,3 ед. за 1 тонну. Стоимость перевозки 1 тонны груза дана в таблице:
Найти наиболее экономичный способ доставки груза из пункта А в пункт В. 9.На схеме дана информационная сеть. Числа в скобках дают вероятность искажения информации при использовании данного канала.
Найти самый надежный путь пересылки сообщения из s в t, считая, что искажения информации при использовании разных каналов не зависят друг от друга. 10.Напишите процедуру, строящую кратчайший vi-vj -путь, использующую в качестве исходных данных матрицу ПРЕД (см. алгоритм 6.9). 11.Найдите кратчайшие пути между всеми парами узлов в сети, заданной матрицей: A= 12.Модифицируйте алгоритм Флойда для нахождения максимальных путей между всеми парами узлов в заданной сети. Сформулируйте условия, которым должна удовлетворять сеть, при которых имеет смысл решать эту задачу. 13.Предложите алгоритм вычисления minmax расстояний между всеми парами узлов заданной сети, имеющий сложность O(n3). Аналогичный вопрос для вычисления maxmin расстояний. Опишите процедуру построения соответствующих кратчайших путей между всеми парами узлов. Предполагается, что сеть задана матрицей ПРЕДШ. 14.Исследуйте задачу построения минимального по числу дуг пути в maxmin-задаче о кратчайшем пути. 15.Предложите алгоритм, который по данной (n 16.Предложите алгоритм, который распознавал бы, имеется или нет в данной сети с произвольными весами дуг контур отрицательной стоимости.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
 n, в которой ПРЕД[i,j] дает номер узла, являющегося предпоследним в кратчайшем vi-vj- пути (понятно, что последним узлом в таком пути является узел vj). Если k=ПРЕД[i,j], то, посмотрев значение ПРЕД[i,k], получим следующий узел в vi-vj-пути. Таким образом, двигаясь по элементам матрицы ПРЕД, легко построить путь для любой пары узлов.
n, в которой ПРЕД[i,j] дает номер узла, являющегося предпоследним в кратчайшем vi-vj- пути (понятно, что последним узлом в таком пути является узел vj). Если k=ПРЕД[i,j], то, посмотрев значение ПРЕД[i,k], получим следующий узел в vi-vj-пути. Таким образом, двигаясь по элементам матрицы ПРЕД, легко построить путь для любой пары узлов.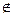 Е. Еще раз повторим, что неотрицательность весов дуг не предполагается, но считается, что в сети нет контуров отрицательной длины.
Е. Еще раз повторим, что неотрицательность весов дуг не предполагается, но считается, что в сети нет контуров отрицательной длины. V. матрица ПРЕД, в которой ПРЕД[v] равно номеру предпоследнего узла в кратчайшем vi-vj -пути.
V. матрица ПРЕД, в которой ПРЕД[v] равно номеру предпоследнего узла в кратчайшем vi-vj -пути.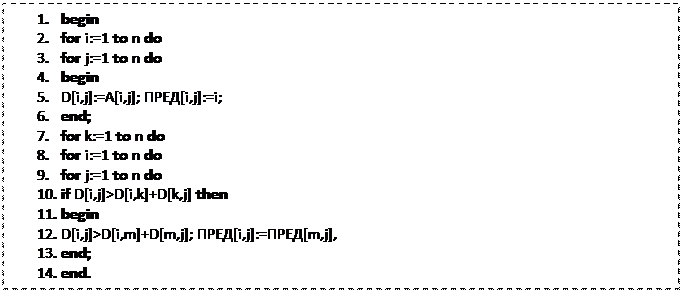
 Завершим главу рассмотрением примера, иллюстрирующего работу алгоритма Флойда.
Завершим главу рассмотрением примера, иллюстрирующего работу алгоритма Флойда.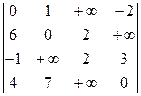 ПЕРЕД=
ПЕРЕД= 
 ПЕРЕД=
ПЕРЕД= 
 ПЕРЕД=
ПЕРЕД= 
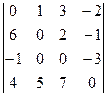 ПЕРЕД=
ПЕРЕД= 
 T=Ø. Требуется среди всех путей, начинающихся в каком-нибудь узле множества S и заканчивающихся в каком-нибудь узле из множества Т. найти путь минимальной стоимости. Свести эту задачу к задаче о кратчайшем пути между фиксированными узлами.
T=Ø. Требуется среди всех путей, начинающихся в каком-нибудь узле множества S и заканчивающихся в каком-нибудь узле из множества Т. найти путь минимальной стоимости. Свести эту задачу к задаче о кратчайшем пути между фиксированными узлами.
