|
|
Сложность задачи сортировкиРассмотрим задачу сортировки в общем виде, когда информацию о последовательности элементов можно получать только с помощью операции сравнения двух элементов. Пусть а1,...,аn - последовательность сортируемых элементов. Не ограничивая общности, можно считать, что элементы заданной последовательности помещены в некоторый массив А в том же порядке, m есть A[i] = a, (i = 1,2,...,n). Начнем с простейшего алгоритма сортировки данных, называемого алгоритмом сортировки выбором. Формализованное описание этого алгоритма представлено ниже.
АЛГОРИТМ 3.1. СОРТИРОВКА ВЫБОРОМ Данные: массив А[1..n]. Результат: массив А[1..n] такой, что А[1] ≤ А[2] ≤ ... ≤ A[n]. 1. begin 2. procedure MIN(i): 3. begin for j = i to n do 4. if A[i] < A[j] then A[i]↔A[j]; 5. end; 6. begin (* главная программа *) 7. for i := 1 to n-1 do MIN(i); 8. end; 9. end. Алгоритм 3.1 имеет следующую структуру. Процедура MIN(i) выбирает минимальный элемент из массива аi,...,аn и ставит его на первое место, т.е. на место ai. Алгоритм начинает работу с вызова процедуры MIN(l), которая перемещает на первое место наименьший элемент исходного массива. Далее процедура повторяется для массива а2,...,аn и т.д.
Теорема 3.1.Алгоритм СОРТИРОВКА ВЫБОРОМ имеет вычислительную сложность O(n2). □ Действительно, в процедуре MIN(i) осуществляется (n-i) операции сравнения и, в худшем случае, (n-i) операции обмена. Значит, общее число шагов, выполняемое процедурой MIN(i) пропорционально (n-i). Отсюда, число шагов алгоритма пропорционально (n - 1) + (n — 2) + ... + 1 = n(n - 1 )/2, то есть сложность алгоритма есть O(n2). Легко видеть, что число сравнений в алгоритме СОРТИРОВКА ВЫБОРОМ в точности равно n(n- 1)/2 , т.е. имеет порядок n2,как и сложность всего алгоритма. Ситуация эта не случайна, так как мы рассматриваем задачу сортировки в предположении, что информацию об элементах можно получать только с помощью операций сравнения. Поэтому в дальнейшем, оценивая сложность того или иного алгоритма, будем учитывать только операции сравнения, поскольку именно они и определяют сложность алгоритма. Следующая теорема дает оценку снизу сложности любого алгоритма сортировки. Теорема 3.2.В любом алгоритме, упорядочивающем с помощью сравнений, на упорядочение последовательности из n элементов тратится не менее c∙n∙loqn сравнений при некотором с > 0 и достаточно большом n. Любой алгоритм, упорядочивающий с помощью сравнений, можно схематично представить в виде корневого дерева (см. параграф 2.1.), называемого двоичным деревом решений. Это дерево можно рассматривать как блок-схему алгоритма сортировки, в котором показаны все сравнения элементов и исходы алгоритма. Вершины дерева (кроме листьев) соответствуют сравнениям элементов, при этом корень дерева соответствует первому сравнению, осуществляемому алгоритмом. Сыновья вершин изображают возможные исходы сравнения отца. Листья соответствуют исходу алгоритма. На рис 3.1 изображено дерево решений алгоритма СОРТИРОВКИ ВЫБОРОМ для сортировки последовательности из трех элементов а1,а2,а3. Здесь запись а:b означает сравнение элементов а и b. После сравнения а и b идем по левой дуге при а ≤ b и по правой при а ≥ b. Вообще говоря, исходом работы алгоритма явится последовательность из трех элементов такая, что а1 ≤ а2 ≤ а3, однако окончательное значение а1 может (за счет операции переприсваивания) отличаться от исходного. На рис. 3.1 листья изображают возможные исходы относительно начальных значений переменных.
В любом таком дереве решений каждая перестановка определяет единственный путь от корня к листу. Поскольку алгоритм сортировки должен различать все возможные перестановки, получаем, что дерево решений должно содержать как минимум n! листьев. При каждом входе алгоритм проходит весь путь от корня до листа, соответствующего данному входу. Следовательно, число операций сравнения, осуществляемое алгоритмом, равно длине пути от корня до листа, то есть равно высоте двоичного дерева решений. Таким образом, высота этого дерева дает оценку снизу сложности алгоритма. Поскольку, всякое двоичное дерево высоты к имеет не более 2к листьев (лемма 2.1), то получаем, что должно выполняться неравенство 2к > n!, так как листьев в двоичном дереве решений должно быть не меньше, чем перестановок из n элементов. Отсюда, k > logn!. Осталось заметить, что при n > 1 справедлива следующая цепочка неравенств:
n! ≥ n(n - 1 )(n - 2)... ( log n! ≥ log( n/2 )n/2 = n/2 log n/2 ≥ n/4 log n Итак, k ≥ n/4 logn — полученное неравенство завершает доказательство теоремы 3.2.
Алгоритм СОРТДЕРЕВО Оказывается, полученная оценка снизу для сложности алгоритмов сортировки не может быть улучшена, а именно, существуют алгоритмы сортировки, имеющие сложность O(nlogn). Один из таких алгоритмов, называемый СОРТДЕРЕВО, мы сейчас разберем. Помимо того, что это полезный алгоритм упорядочения, к тому же теоретически наилучший, в нем используется интересная структура данных, полезная и в других ситуациях. Алгоритм СОРТДЕРЕВО был предложен в 1964 году независимо Уильямсом (под названием Heapsort) и Флойдом (Treesort). Иногда, например, в [6], этот алгоритм называют алгоритмом пирамидальной сортировки. В массиве А[1..n] введем структуру корневого двоичного дерева. считая, что в корне находится элемент А[1], и элемент A[i] имеет двух сыновей: A[2i] (если 2i ≤ n) и A[2i+1] (если 2i+1 < n).- Такую структуру назовем двоичным деревом массива А.
Лемма 2.1.Двоичное дерево массива длины n имеет высоту □ Напомним (см. гл.2), что высота корневого дерева есть по определению длина самого длинного пути из корня до какого-нибудь листа. Например, на рис.3.2 это путь до листа, в котором находится число 7. Легко видеть, что длина этого пути равна 3.
Пусть k - высота двоичного дерена массива длины n. Для всех s < k в дереве имеется ровно 2s вершин глубины s. Пусть h — количество вершин глубины k. Тогда справедливо неравенство 1 < h < 2k. Поскольку число вершин равно n — длине массива, то справедливо равенство: n = 1 + 2 + ... + 2k-1 + h = 2k - 1 + h. Учитывая, что h ≤ 2k, получаем, что n = 2k - 1 + h ≤ 2k - 1 + 2k < 2k+1. Отсюда n < 2k+1. С другой стороны, так как h ≥ 1, то n= 2k - 1 + h ≥ 2k. Таким образом, справедливо неравенство 2k ≤ п ≤ 2k+1. Отсюда, k ≤ logn ≤ k+1, то есть k = Двоичное дерево массива А называется сортирующим деревом массива А, если выполняются условия: А[k] ≥ А[2 k] и А[k] ≥ А[2 k +1] для к = l,2,... Непосредственно из определения вытекает, что наибольший элемент массива находится в корне его сортирующего дерева. Легко видеть также, что двоичное дерево, изображенное на рис. 3.2, не является сортирующим. Именно на представлении массива сортирующим деревом основан один из теоретически наилучших алгоритмов сортировки данных — СОРТДЕРЕВО. Изложим вначале основные принципы работы этого алгоритма. На первом этапе элементы массива А переставляются так, чтобы выполнялось свойство (*) сортирующего дерева, иначе говоря, двоичное дерево массива А преобразуется в сортирующее. Процедуру, осуществляющую это преобразование, будем называть ПСД. Затем, поскольку по свойству сортирующего дерева, элемент в корне, а именно, А[1] является наибольшим в А, то, переставляя А[1] и А[n], и удаляя А[n] из дерева, получим массив А[1..п-1] и A[n] = max А[1..n]. Теперь преобразуем А[1..n-1] в сортирующее дерево, затем переставим А[1] и А[n-1] и удалим А[n-1]. Процесс продолжается до тех пор, пока в сортирующем дереве не останется один элемент. Тогда А[1],...,А[n] — упорядоченная по неубыванию последовательность. Перейдем к формальному описанию алгоритма СОРТДЕРЕВО. Начнем с описания процедуры ПСД (построение сортирующего дерева). В его основе лежит рекурсивная процедура ПЕРЕСЫПК(i,j), имеющая параметры i и j. Они задают область ячеек массива А, которая в результате процедуры ПЕРЕСЫПКА будет обладать свойством сортирующего дерева, при этом его корень помещается в вершину i. Неформально можно сказать, что построение сортирующего дерева идет снизу вверх, начиная с листьев, и справа налево, строя при этом все большие и большие сортирующие поддеревья. Действительно, все листья уже являются сортирующими поддеревьями. В общем случае, когда мы находимся в вершине i, поддеревья с корнями 2i и 2i+l уже являются сортирующими. Если выполняются неравенства A[i] ≥ A[2i] и A[i] ≥ A[2i+1], то дерево с корнем в i является сортирующим, и его построение с корнем в вершине i закончено. Если хотя бы одно из этих неравенств не выполнено, то переставляем A[i] и А[к], где к — тот сын i, который содержит наибольшего из элементов A[2i] и A[2i+1], Пусть, например, k = 2i, тогда поддерево с корнем в вершине 2i + 1 останется сортирующим, но может «испортиться» поддерево с корнем в вершине 2i. Для него мы повторяем эту процедуру, которая и называется ПЕРЕСЫПКА(i,j). Второй параметр j задает длину массива, в котором выполняется эта процедура. Разумеется, при перестройке двоичного дерева в сортирующее этот параметр равен n, так как работа выполняется для всего массива А. В дальнейшем, при упорядочении массива А второй параметр j будет меняться. Ниже дано формальное описание процедур ПЕРЕСЫПКА и ПСД. Без формального описания используется функция MAXCЫH(i), значением которой является тот сын i, который содержит наибольший из элементов A[2i] и A[2i+1], Структура этой процедуры следующая. В строке 2 осуществляется проверка, является ли узел с номером i листом или нет. В строке 4 проверяется условие (*) для дерева с корнем в узле с номером i, и если оно не выполнено, то переставляется элемент в корне дерева с наибольшим из элементов в его сыновьях, и вновь вызывается процедура ПЕРЕСЫПКА, но уже с другим параметром. procedure ПЕРЕСЫПКА( i ,j); 1. begin 2. if i ≤ 3. begin k := MAXCЫH(i); 4. if A[i] < A[k] then 5. begin 6. A[i]↔ A[k]; ПЕРЕСЫПКА(k,j) 7. end; 8. end; 9. end; Процедура ПСД, строящая сортирующее дерево массива А, выглядит следующим образом. procedure ПСД; 1. begin 2. for i := 3. end Разберем пример, иллюстрирующий работу обеих этих процедур Пусть задан числовой массив А[1…10]:
Все перестановки элементов массива, осуществляемые процедурой ПЕРЕСЫПКА, будем отображать в двоичном дереве изменяющегося массива. Для краткости, на схеме вместо ПЕРЕСЫПКА(i,10) будем писать П(i).
Изобразим окончательный результат в виде таблицы:
Алгоритм упорядочения, основанный на понятии сортирующего дерева, может быть формально записан следующим образом:
АЛГОРИТМ 3.2. СОРТДЕРЕВО Данные: массив элементов А[1..n]. Результат: массив элементов А[1..n], упорядоченный по неубыванию, то есть А[1] ≤ А[2] ≤ ... ≤ А[n]. 1. begin 2. ПСД; (* вначале строится сортирующеедерево *) 3. for i := n downto 2 do 4. begin 5. A[l] ↔ A[i]; 6. ПЕРЕСЫПКА( 1,i-1) 7. end; 8. end
На рис.3.4 дерево f) является сортирующим деревом исходного массива А, полученным в результате работы процедуры ПСД. Затем происходит перестановка А[1] и А[10] (дерево g) ). К дереву g) применяется процедура ПЕРЕСЫПКА(1,9), в результате которой число 3 проходит путь по правым ветвям из корня дерева до листа. Затем вновь происходит перестановка корня с листом и т.д. В результате получится массив А, упорядоченный по возрастанию.
Теорема 3.3.Алгоритм упорядочения СОРТДЕРЕВО имеет вычислительную сложность O(nlogn). □ Естественно считать размером задачи сортировки длину массива элементов — n. Найдем вначале сложность процедуры ПСД. Пусть k — высота двоичного дерева исходного массива А. По лемме 3.1 имеем равенство к = Через T(k-i) обозначим сложность процедуры ПЕРЕСЫПКА, выполняемой из всех вершин глубины k-i. Тогда сумма Σ = Т(k-1) + Т(k-2) + ... +Т(0) равна сложности всей процедуры, строящей сортирующее дерево, поскольку ПЕРЕСЫПКА начнет выполняться с вершин глубины k-1. Пусть вершина i имеет глубину k-1 и (возможно) двух сыновей: 2i и 2i+l. Пересыпка из вершины заключается в сравнении трех чисел: A[i], A[2i], A[2i+1] и, если это необходимо, перестановки A[i] с наибольшим из A[2i] и A[2i+1], Ясно, что сложность пересыпки из вершины i не зависит от п и оценивается сверху константой с. Тогда справедливо неравенство Т(k — 1) ≤ с 2k-1, так как имеется ровно 2k-1 вершина глубины k-1. Переходя на более высокий уровень, т.е. рассматривая вершины глубины k-2, заметим, что справедливо неравенство Т(к - 2) ≤ с 2k-2 + 1/2 Т(k — 1), так как после сравнения этого элемента в вершине глубины k-2 с элементами в ее сыновьях дальнейшая пересыпка пойдет только не более, чем из одного сына. Аналогично, T(k - i) ≤ с 2k-1 + 1/2 Т(к - i + 1) для всех i ≤ k. Отсюда, Σ = Т(k - 1) + Т(k - 2) +...+ Т(0) ≤ с 2k-1 + с 2k-2 +...+ с + +1 /2 Т(k - 1) + 1 /2 Т(k - 2)+...+1 /2 Т(1) ≤ с (2k-1 +2k-2+...+1)+1 /2Σ. Значит, Σ ≤ с (2k-1 + 2k-2 +...+1) < 2с 2k < 2 с n, так как 2k ≤ n. Итак, доказано неравенство: Σ ≤ 2сn. Это означает, что сложность процедуры ПСД есть О(n), то есть она линейна. Осталось оценить сложность основного цикла в строках 3-7 алгоритма СОРТДЕРЕВО. Для этого достаточно оценить сложность процедуры ПЕРЕСЫПКА(1 ,n-1). Элемент в корне А[1] сравнивается с элементами в его сыновьях А[2] и А[3]. Эту сложность мы ранее обозначали константой с. Затем (если произошла перестановка) нужно повторить операции сравнения, считая корнем того сына, в котором произошла перестановка. В худшем случае перестановки и сравнения будут происходить до тех пор, пока элемент не вытолкнется в лист. Путь, пройденный элементом, имеет длину Отсюда, сложность цикла в строках 3-7 есть O(nlogn). Окончательно, сложность алгоритма СОРТДЕРЕВО есть О(n) + O(logn) = O(nlogn). □
ЗАДАЧИ 1. (Алгоритм БЫСТРОСОРТ) Заданную последовательность элементов S = {а1,а2,...,аn} можно упорядочить следующим образом. Выбрать произвольный элемент а, разбить S на три последовательности S1, S2, соответственно меньших а, равных а и больших а. Затем повторить ту же процедуру к S1 и к S3 . Напишите на упрощенном Паскале рекурсивную и нерекурсивную версии этого алгоритма. Докажите, что его сложность есть O(n2). Несмотря на то, что сложность алгоритма БЫСТРОСОРТ есть O(n2), то есть хуже, чем у алгоритма СОРТДЕРЕВО, БЫСТРОСОРТ предпочтительней, вообще говоря, с точки зрения практики. Дело в том, что сложность вычисляется в худшем случае, однако в среднем БЫСТРОСОРТ имеет сложность O(nlogn). Понятие сложности в среднем изложено в книге [6], там же дано детальное описание как рекурсивной, так и нерекурсивной версий этого алгоритма. 2. а) (Сортировка обменами) Последовательным просмотром элементов а1,...,аn найти первое к такое, что аk > аk+1. Поменять аk и аk+1 возобновить просмотр последовательности, начиная с аk+1 и так далее. В результате наибольший элемент передвинется на последнее место. Следующие просмотры начинать с а1 уменьшая на единицу количество просматриваемых элементов. Последовательность будет упорядочена после просмотра, в котором либо не произошло ни одной перестановки, либо участвовали первый и второй элементы. б) (Сортировка простыми вставками) Просматривать последовательно а2,...,аn, и каждый новый элемент аk вставлять на подходящее место в уже упорядоченную последовательность a1,...,ak-1. Это место определяется последовательным сравнением аk с элементами a1,...,ak-1. Напишите на упрощенном Паскале алгоритмы сортировки обменами и простыми вставками. Докажите, что сложности этих алгоритмов — О(n2). 3. Исследовать число сравнений и число перестановок элементов a1,...,an для алгоритмов сортировки выбором, обменами и простыми вставками. Докажите, что число перестановок в алгоритме сортировки выбором есть О(n). В то же время и число сравнений для сортировки выбором, и обе указанные характеристики для сортировок обменами и простыми вставками есть O(n2). В частности, это означает, что сортировка выбором предпочтительней сортировки обменами и сортировки простыми вставками в тех случаях, когда перестановка элементов является существенно более сложным делом, чем их сравнение. Например, такая ситуация имеет место в задаче: упорядочить строки заданной матрицы размером n 4. Даны пять попарно различных чисел: а, b, с, d, е. Упорядочить их по возрастанию, используя для этого не более семи сравнений. 5. (Сортировка вычерпыванием). Дана последовательность целых чисел a1,a2,...,an, заключенных между 0 и m-1. Если т не очень велико, то ее можно упорядочить следующим образом: 1. Организуем m пустых очередей: по одной для каждого целого числа от 0 до m-1. 2. Последовательно просматривая исходную последовательность a1,a2,...,an, помещаем элемент аk в очередь с номером k. 3. Сцепим очереди (содержимое (k+1)-ой очереди припишем к концу k-ой очереди). В результате получим упорядоченную по возрастанию последовательность. Докажите, что этот алгоритм имеет сложность О(п). 6. Пусть двоичное дерево массива А[1..n] является его сортирующим деревом, и все А[k] попарно различны. Как найти второй по величине элемент этого массива? А третий? Какую глубину может иметь в сортирующем дереве вершина, содержащая k-ый по величине элемент массива А?
Глава IV Поиск в графе Многие алгоритмы на графах основаны на систематическом переборе всех вершин графа, при котором каждая вершина просматривается в точности один раз, при этом переход от уже рассмотренной вершины к еще не рассмотренной вершине осуществляется по ребрам графа. В этой главе мы рассмотрим два стандартных, широко используемых на практике метода такого перебора: поиск в глубину и поиск в ширину. Опишем оба этих метода поиска только для неориентированных графов. Модификация этих методов для случая орграфов тривиальна.
Поиск в глубину. Идея этого метода поиска состоит в следующем. Поиск начинается с некоторой фиксированной вершины v, называемой корневой вершиной поиска или корнем. При этом считаем v просмотренной вершиной. Затем выбираем какое-нибудь ребро {v,w}, инцидентное v, проходим его и попадаем в вершину w. Тот факт, что в процессе поиска использовано именно ребро {v,w} отмечается обычно следующим образом. Ребро {v,w} ориентируется из v в w. полученную дугу (v,w) считают дугой корневого дерева с корнем v. Такое дерево называется ПВГ-деревом с корнем v, или короче ПВГ(v)—деревом. При переходе от v к w, вершина v объявляется отцом вершины w и обозначается OTEЦ[w], вершина w объявляется просмотренной, и поиск продолжается из вершины w. В общем случае, когда мы находимся в некоторой вершине v, возникают две возможности: 1. Все вершины, смежные с v, уже просмотрены. В этом случае возвращаемся к вершине ОТЕЦ[v] и продолжаем поиск из нее, а вершину v с этого момента считаем использованной. 2. Существует еще не просмотренная вершина w, смежная с вершиной v. Тогда ребро {v,w} превращаем в дугу (v,w), добавляя ее к ПВГ(v)-дереву; полагаем ОТЕЦ[w]=v; проходим по дуге из v в w и продолжаем поиск из w. Поиск в глубину завершается тогда, когда все вершины графа будут просмотрены. Здесь возможны две ситуации: 1. Корневая вершина использована (т.е. все смежные с ней вершины просмотрены), однако в графе еще есть непросмотренные вершины. В этом случае выбираем произвольную непросмотренную вершину, объявляем ее корнем и вновь начинаем поиск уже из этой вершины. Такая ситуация возникает только в случае несвязного графа. 2. Корневая вершина и все другие использованы. Поиск на этом заканчивается. Представим формальное описание изложенного алгоритма. Массив МЕТКА, используемый в алгоритме имеет по одному элементу для каждой вершины графа и служит указателем на то, что просмотрена или нет данная вершина. Считаем, что METKA[v]=0, если v не просмотрена, и METKA[v]=l в противном случае. Массив ОТЕЦ описан ранее. Понятно, что он имеет длину n, где n — число вершин в графе. В множестве Т будем хранить дуги ПВГ-деревьев. Вначале изложим версию алгоритма поиска в глубину, основанную на рекурсивной процедуре ПВГ(v) — поиск в глубину из вершины v.В рассматриваемом алгоритме связность графа непредполагается.
АЛГОРИТМ 4.1. ПОИСК В ГЛУБИНУ Данные: неориентированный граф G=(V,E), заданный списками смежностей ЗАПИСЬ[v]. Результаты: массив ОТЕЦ, множество Т. 1. procedureПВГ (v); (*поиск в глубину с корнем v) 2. beginMETKA[v]:=1; 3. for w 4. ifMETKA[w]=0 then 5. beginOTEЦ[w]:=v; T:=T 6. end; 7. end; 8. begin (*Главная программа) T := Ø; 9. forv 10. forv 11. ifMETKA[v]=0 then 12. beginOTEЦ[v]:=nil; ПВГ(v); 13. end; 14. end.
В просмотренном графе G дуги ПВГ-деревьев обозначены стрелками в соответствии с ориентацией, полученной в ходе поиска. Такие дуги часто называют прямыми дугами поиска. Прочие ребра графа, называемые иногда обратными дугами поиска, обозначены на рисунке пунктирами. Числа в скобках, стоящие у вершин просмотренного графа, соответствуют очередности, в которой они просматривались в ходе поиска. Отметим, что вершины с номерами 1, 9 и 11 являются корнями ПВГ-деревьев. Разберем теперь нерекурсивную версию процедуры ПВГ(v). Рекурсия устраняется стандартным способом с помощью стека. Каждая вершина помещается в стек сразу, как только будет достигнута, то есть просмотрена, и удаляется из стека после того, как будет использована. Поиск новой непросмотренной вершины ведется из той вершины, которая последней попала в стек. Для организации такого процесса понадобится дополнительно массив указателей УКАЗ длины n, где n=|V|. Предполагается, что в начале работы процедуры поиска выполняются равенства УKA3[v]=HAЧAЛO[v], для всех v из V, иначе говоря, УКАЗ[v] дает адрес первой записи в списке ЗАПИСЬ[v]. В процессе работы процедуры поиска УКАЗ[v] меняется таким образом, что указывает на следующую запись в списке ЗАПИСЬ[v] после той, которая содержит последнюю просмотренную из нее вершину. Смысл переменных МЕТКА, ОТЕЦ и Т тот же, что и ранее.
Теорема 4.1.Сложность алгоритма 4.1 ПОИСК В ГЛУБИНУ есть O(n+m). Понятно, что цикл в строке 10 (инициализация) требует n операций. Далее, проверка условия, стоящего в строке 13, осуществляется ровно n раз. Вызов процедуры ПВГ(v) влечет за собой просмотр всех вершин связной компоненты графа, содержащей v При этом каждая вершина из связной компоненты просматривается ровно один раз, поскольку просматриваются (т.е, выполняется строка 5) только те вершины w, для которых справедливо равенство METKA[w]=0, а сразу после просмотра, в результате вызова ПВГ(w), имеем равенство METKA[w]=l. В тот момент, когда мы находимся в какой-либо вершине v, для поиска новой, еще не просмотренной вершины w, смежной с v, требуется анализировать ребра, инцидентные v. В процедуре ПВГ1(v) подробно описано, что это можно сделать, используя массив УКАЗ так, что каждое ребро графа анализируется ровно два раза: от v к w и от w к v. Следовательно, при работе алгоритма 4.1 анализируются все ребра и все вершины графа, каждое не более двух раз. При каждом анализе количество операций ограничено константой. Отсюда сложность алгоритма 4.1 есть O(n+m). Как уже отмечалось выше алгоритм 4.1 различает связные и несвязные графы. Легко модифицировать этот алгоритм (а именно, каждый раз при выполнении условия в строке 13 заводить новое множество Т) так, чтобы он вычислял связные компоненты графа. Из этого замечания и теоремы 4.1 вытекает Следствие. Связные компоненты неориентированного графа могут быть найдены за время O(n+m). Поиск в глубину в ориентированном графе отличается от поиска в неориентированном графе только тем, что ребра проходятся в соответствии с их ориентацией. Поскольку в главе 2 мы условились считать, что в списке ЗАПИСЬ[у] встречаются только те вершины w, для которых (v,w)
Поиск в ширину. Другое название этого популярнейшего метода — волновой алгоритм. Причины появления такого названия станут ясны из дальнейшего. Поиск в ширину начинается с некоторой фиксированной вершины v, называемой корнем. Вершину v считаем просмотренной и помещаем ее в организуемую нами очередь. Считаем также, что вершина v образует нулевой фронт распространения волны. Затем проходим все ребра {v,w}, инцидентные v, в каком-нибудь порядке и ориентируем их из v в w. Вершины w, смежные с v, считаем просмотренными и размещаем их в порядке просмотра ребер в очередь. Для всех таких вершин w полагаем OTEЦ [w]:=v и говорим, что w просмотрена из v. Ориентированные ребра (v,w) будем называть ребрами ПВШ(v)-дерева. Говорят часто, что все такие вершины w образуют первый фронт распространения волны. Вершина v после этих действий считается использованной и удаляется из очереди. Дальнейший поиск продолжается следующим образом. Берем очередную вершину v из очереди, проходим по всем ребрам, инцидентным v, которые соединяют вершину v с еще непросмотренными вершинами w. Все такие вершины w объявляются просмотренными, для них полагают OTEЦ[w]:=v, ребра (v,w) относят к ПВШ(v)-дереву. После этих действий вершина v считается использованной и удаляется из очереди. Говорят также, что вершины, просмотренные из вершин, принадлежащих фронту с номером k, образуют (k+1)-ый фронт распространения волны. Завершается поиск в ширину с корнем в заданной вершине таким же образом, как и поиск в глубину, а именно тогда, когда ни одной новой вершины просмотреть не удается.
Отметим, что в ПВШ(1) - дереве поиска вершины 2, 3, 4 образуют первый фронт распространения волны, вершины 5, 6 и 7 — второй, а вершина 8 — третий.
АЛГОРИТМ 4.2. ПОИСК В ШИРИНУ Данные: неориентированный граф G=(V,E), заданный списками смежностей. Результаты: массив ОТЕЦ, множество D.
В приведенном формальном описании алгоритма поиска в ширину переменная МЕТКА имеет тот же смысл, что и ранее в алгоритме 4.1. Дуги ПВШ-деревьев хранятся в множестве D. Смысл переменной ОТЕЦ объяснен выше. Просмотренные вершины помещаются в ОЧЕРЕДЬ и удаляются оттуда сразу после их использования (строка 4 алгоритма). В алгоритме 4.2 связность графа не предполагается. Для корневых вершин поиска и только для них выполняется равенство ОТЕЦ[v]=nil. Точно также как и ранее теорема 4.1 доказывается Теорема 4.2.Алгоритм 4.2 ПОИСК В ШИРИНУ имеет вычислительную сложность O(n+m). Цепи и пути в графах. В этом разделе будем рассматривать только связные неориентированные графы. Нетрудно проверить, что и ПВГ-дерево, и ПВШ-дерево действительно являются деревьями, и более того — корневыми деревьями (см. гл.2), причем корнями этих деревьев являются те вершины, с которых начинался поиск (собственно поэтому они и в ПВГ и в ПВШ названы корневыми вершинами). Ранее, в главе 2, мы условились считать, что если в ориентированном графе имеется дуга (v,w), то v — отец w, a w — сын v. Легко видеть, что даваемые алгоритмами 4.1 и 4.2 значения переменных ОТЕЦ[w] согласуются с ранее введенным понятием, а именно, если v=ОТЕЦ[w], то (v,w) Напомним, что вершина v называется предком вершины w. и, соответственно, w — потомком v, если в корневом дереве существует путь от v до w. Например, в корневом дереве ПВШ(1) из рис.4.2 вершина 8 является потомком вершины 2. В следующей теореме формулируются полезные свойства ПВГ-деревьев. Теорема 4.3.Пусть Т — ПВГ-дерево связного неориентированного графа G=(V,E), и пусть {u,w} Предположим без ограничения общности, что вершина и будет просмотрена раньше, чем w. Рассмотрим процесс поиска в глубину, начиная с первого вызова процедуры ПВГ(u) (см. алгоритм 4.1.), и до первого вызова ПВГ(w). Это означает, что мы прошли по некоторым ребрам из вершины u в w. Но именно эти пройденные ребра мы и относим в ПВГ-дерево Т. Они образуют путь из u в w, следовательно, вершина u является предком вершины w в корневом дереве Т. Понятно, что ПВШ-дерево не обладает свойством, сформулированным в теореме 4.3. Например, в ПВШ(1)-дереве, изображенном на рис.4.2, ни вершина 3 не является потомком вершины 6, ни вершина 6 не является потомком вершины 3 (говорят, что такие вершины несравнимы в корневом дереве). Как в ПВГ-дереве, так и в ПВШ-дереве для каждой вершины w, существует единственный путь из корня v в w. Как построить этот путь? Это несложно делается с помощью массива ОТЕЦ. Отметим только, что под путем в орграфе мы договорились понимать в зависимости от степени удобства, либо последовательность ребер, либо последовательность вершин (см.гл.2). В предлагаемом ниже алгоритме 4.3 требуемый путь идентифицируется последовательностью вершин. Предполагается, что перед работой этого алгоритма работала либо процедура ПВГ(v), либо процедура ПВШ(v).
АЛГОРИТМ 4.3. ПОСТРОЕНИЕ ПУТИ Данные: корневая вершина поиска v, вершина w. массив ОТЕЦ.
Понятно, что последовательность вершин v=v0,v1,...,vk=w, полученная считыванием СТЕКА, образует как v-w-путь в корневом дереве Т (или D), так и v-w-цепь в исходном графе G. Оказывается, что пути, построенные поиском в ширину, обладают очень полезным свойством, а именно, справедлива. Теорема 4.4.Пусть D — ПВШ-дерево с корнем v связного неориентированного графа G=(V,E). Тогда для любой вершины w Пусть кратчайшая по числу ребер v-w-цепь в графе G содержит t ребер. (Будем говорить, что вершина w находится на расстоянии t от v). Докажем теорему индукцией по расстоянию t. Пусть t=l. Тогда всякая вершина u, находящаяся на расстоянии 1 от v, будет просмотрена из v, то есть для всех таких вершин u справедливо равенство ОТЕЦ[u]=v. Одновременно v — единственная вершина связного графа, для которой OTEЦ,[v]=nil. Значит, как это следует из алгоритма 4.3, поиск в ширину правильно определяет кратчайшие цепи до всех вершин, находящихся на расстоянии 1 от вершины v. Пусть ПВШ-дерево правильно определяет кратчайшие цепи до всех вершин, находящихся на расстоянии t ≤ k от v. Пусть вершина w находится на расстоянии k+1 от v и путь v=v0,v1...,vk+1=w — кратчайшая v-w-цепьв графе G. Ясно, что цепь v=v0,v1,...,vsявляется кратчайшей v-vs-цепью в графе G для всех s=l,...,k. В частности, вершина vkнаходится на расстоянии k от v. Рассмотрим ПВШ(v)-дерево в тот момент, когда просматривается вершина w, и пусть u=OTEЦ[w]. В силу предположения индукции достаточно доказать, что и находится на расстоянии k от v. Если u=vk то теорема доказана. Пусть u≠vk. Так как ребро {vk,w} Заметим, что пути, определяемые поиском в глубину, вообще говоря, не являются кратчайшими. Например, на рис.4.1 путь от вершины 1 до вершины 8 проходит через вершины 2,3,4,7,6 и имеет длину 6, а поиск в ширину (см.рис.4.2) определяет путь, проходящий через вершины 4,7, длиной 3. Пути в лабиринте. Под лабиринтам будем понимать множество точек на плоскости Р={(х,у) : 1≤х≤n, 1≤у≤m} с целочисленными координатами. Каждая точка р 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
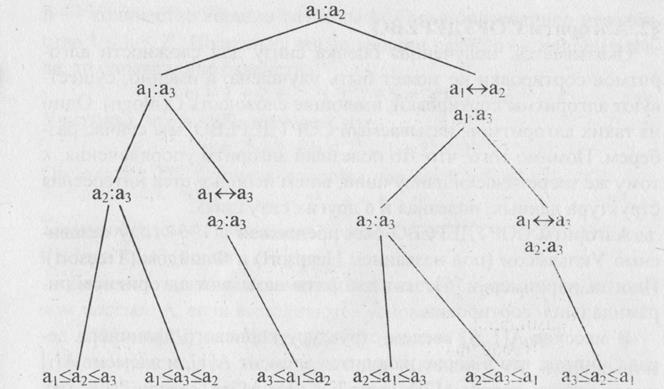Рис. 3.1. Двоичное дерево решений для сортировки трех элементов
) ≥ (n/2)n/2, так что
.
. (*)
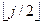then (* если i — не лист *)
Обращаем внимание на работу процедур П(2) и П(1). В процедуре П(2) вначале были переставлены числа 3 и 9 в дереве d), затем была вызвана процедура 11(5), которая переставила 3 и 4. Процедура П( 1) в дереве е) переставила 9 и 2. затем вызвала процедуру П(2), которая переставила 2 и 7 и вызвала П(4), но П(4) уже ничего не переставляла.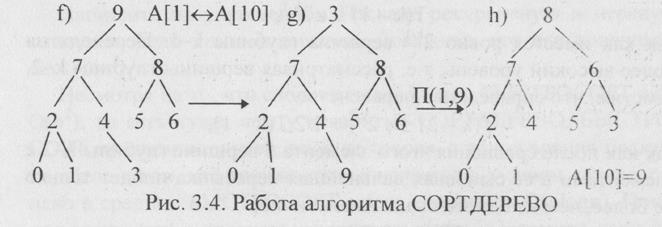
Продолжим рассмотрение ранее начатого примера.
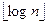,в частности, отсюда следует, что 2k ≤ n.
m в порядке неубывания первых элементов.
ЗАПИСЬ[v] do
{(v,w)}; ПВГ(w);
На рис.4.1 показано, как поиск в глубину исследует неориентированный граф G. Предполагается, что в списках смежности этого графа вершины встречаются в порядке возрастания номеров, и, что цикл в строках 11-14 алгоритма 4.1 выполнялся в порядке возрастания номеров вершин.
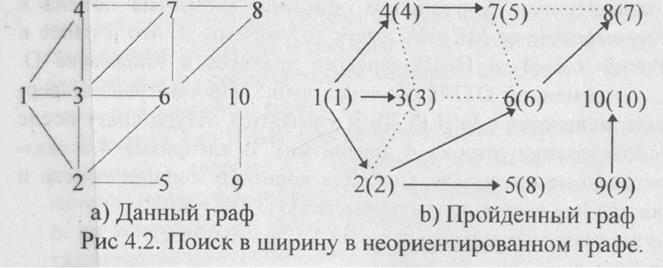На рисунке 4.2 показано, как поиск в ширину исследует граф G, изображенный ранее на рис.4.1. Дуги ПВШ-деревьев изображены стрелками в соответствии с ориентацией, полученной в ходе поиска. Прочие ребра исходного графа изображены пунктиром. Предполагалось, что вершины в ходе поиска просматривались в порядке возрастания их номеров.
Результат: СТЕК, содержащий последовательность вершин, образующих v-w-путь.