
|
|
Определение нагрузок на плитуРасчетные значения нагрузок Fd определяют путем умножения их нормативного значения Fk на частный коэффициент безопасности по нагрузке gF , значения которого приведены в [1, Приложение А, таб.А2]. За приведенную высоту плиты принимаем отношение объема бетона в ней к её площади: hred = 1,69 / 23,8 = 0,07 м.
Таблица 2.1 - Нагрузка на плиту
Напряженно-деформированное состояние ребристой плиты в целом имеет сложный характер, поэтому в практических расчетах плиту расчленяют на отдельные элементы – полку, поперечные и продольные ребра и рассчитывают как самостоятельные элементы.
Расчет полки плиты
Расстояние между осями поперечных ребер равно 1400 мм. Полка представляет собой многопролетную конструкцию с наибольшими размерами поля: l1 = 1400 – 2 × 120 / 2 = 1280 мм,
Рисунок 2.2 - Расчетная модель полки
Соотношение сторон: l2 / l1 = 2670 / 1280 = 2,09. Т.к. l2 / l1 = 2,09 < 3, расчетную модель полки ребристой панели принимаем в виде плиты (одной ячейки рассматриваемой ребристой плиты) с защемлением по четырем сторонам (в рёбрах). На этом основаниирассматриваемую плиту целесообразно армировать сеткой с рабочей арматурой вдоль обоих пролетов.
Таблица 2.2 - Нагрузка на полку плиты
Рассчитываем плиту методом предельного равновесия (кинематический способ) [6, парагр.4]. Плита рассматривается в состоянии предельного равновесия как система плоских звеньев, соединенных между собой по линии излома пластическими шарнирами, возникающими в пролетах снизу - по биссектрисам углов, на опорах сверху - вдоль балок, в середине пролета – вдоль длинной стороны плиты.
Рисунок 2.3 - К расчету плиты, опертой по контуру
Воспользуемся готовой формулой [6, формула (3.30)], выведенной из условия равенства работ внешней нагрузки и внутренних усилий на возможных перемещениях: F × l12 × (3 × l2 - l1) / 12 = (2 × M1 + M3 + M4) × l2 + (2 × M2 + M5 + M6) × l1, (7) где F – полная нагрузка на полку плиты, М1, М2, М3, М4, М5, М6 – моменты на 1 п.м. ширины плиты (рис.2.3). Значения этих моментов находим, пользуясь рекомендуемыми соотношениями между расчетными моментами согласно [6, таб.3.7]. М2 / М1 = 0,4; М3 / М1 = М4 / М1 = 1,6; М5 / М1 = М6 / М1 = 0,6. Подставляя данные значения в формулу (7), получим: 4,879×1,282 × (3×2,67-1,28)/12 = (2×M1+1,6×M1+1,6×M1)×2,67 + (2×0,4×M1+0,6×M1+0,6×M1) ×1,28; 4,483 = 16,444 × M1; M1 = 0,273 кН/м; М2 = 0,273 × 0,4 = 0,109 кН/м; М3 = М4 = 0,273×1,6 = 0,437 кН/м; М5 = М6 = 0,273 × 0,6 = 0,164 кН/м. Арматуру рассчитываем по вычисленным значениям моментов как для изгибаемых элементов прямоугольного сечения. Используя упрощенный деформационный метод расчета сечений, в качестве расчетного момента выбираем наибольший из действующих вдоль каждой стороны плиты. Подберем рабочую арматуру, которая будет располагаться параллельно поперечным рёбрам плиты для полосы шириной 1 м. Вычисляем значение коэффициента αm: αm = Msd / (α · fcd · b · d2). (8) Расчетную рабочую высоту сечения d определяем с учетом толщины защитного слоя и половины диаметра рабочей арматуры (принимая во внимание указания табл.11.4 [1, изм. 3], ориентировочно примем с = 17 мм): d = h – c = 40 – 17 = 23 мм. αm = 0,164 ·106 / 1·20·1000·232 = 0,016. Сравниваем полученное значение с αm,lim: αm,lim = ωс· (εcu/( εsy+ εcu)) · (1- k2 · (εcu/( εsy+ εcu))); (9) εsy = fyd / Еs = 417 / 2·105 = 2,085·10-3; αm,lim = 0,81· (3,5 / (2,085+3,5)) · (1-0,416·(3,5 / (2,085+3,5))) = 0,375; αm = 0,016 < αm,lim = 0,375 => растянутая арматура достигла предельных деформаций. Определяем относительное плечо пары сил η:
Требуемая площадь сечения растянутой арматуры Ast1 = Msd / η · fyd · d; Ast1 = 0,164 · 106 / 0,992· 417·23 = 17,24 мм2. Минимальная площадь рабочей арматуры назначаем с учетом коэффициента армирования ρmin [1, изм.3, таб.11.1]: ρmin = 26 · ρmin = 26· Принимая ρmin = 0,15%, получим: As,min = ρmin · b · d; (11) As,min = 0,0015·1000·23 = 34,5 мм2. As,min = 34,5 мм2 > Ast1 = 17,24 мм2 , принимаем Ast1 = 34,5 мм2. С учетом конструктивных требований (шаг S ≤ 200 мм) принимаем 5Ø4 мм общей площадью 62,8 мм2 с шагом 200 мм. Аналогично подберем рабочую арматуру, которая будет располагаться параллельно продольным рёбрам плиты: αm = 0,437 · 106 / 1· 20 · 1000 · 232 = 0,041; αm = 0,041 < αm,lim = 0,375;
Ast2 = 0,437 · 106 / 0,978 · 417·23 = 46,59 мм2. As,min = 34,5 мм2 ≤ Ast2 = 46,59 мм2. С учетом конструктивных требований (шаг S ≤ 200мм) принимаем 5Ø4 мм общей площадью 62,8 мм2 с шагом 200 мм. Назначаем сетку С-1 из проволоки класса S500 Ø4 мм с шагом S = 200 мм продольных стержней и с шагом S = 200 мм поперечных стержней (15 продольных стержней и 40 поперечных).
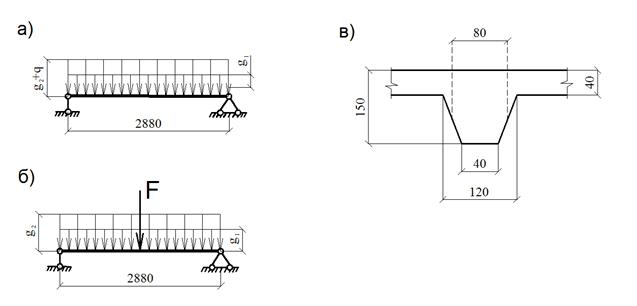
Расчет поперечного ребра Поперечное ребро рассматривается как балка на двух свободных опорах с расчетным пролетом, равным расстоянию между осями продольных рёбер leff = 2,98 - 0,10 = 2,88 м (рис 2.4в).
Рисунок 2.4 - Расчетные схемы и сечение поперечного ребра
Расчетная схема ребра при действии постоянной и снеговой нагрузок приведена на рис.2.4а. Постоянная расчетная нагрузка на ребро: - от собственного веса ребра (без учета полки) g1 = 0,08 · 0,11 · 2500 · 10 · 1 · 1,35 = 297 Н/м = 0,297 кН/м; - передаваемая полкой плиты g2 = 3,079 · 1,4 = 4,31 кН/м; - расчетная снеговая нагрузка на ребро gsd = 1,2 · 1,4 = 1,68 кН/м; Расчетный изгибающий момент в пролете: Мsd = ((g1 + g2 + gsd) · leff2) / 8; (12) Мsd = ((0,297 + 4,31 + 1,68) · 2,882) / 8 = 6,52 кНм. Поперечная сила у опор: Vsd = (( g1 + g2 + gsd) · leff) / 2; (13) Vsd = (( 0,297 + 4,31 + 1,68) · 2,88) / 2 = 9,05 кН. Расчетные усилия в ребре от постоянной нагрузки и сосредоточенной от веса рабочего с инструментом Fsd = 1 · 1,5 = 1,5 кН (рис 2.4б). Мsd = ((g1 + g2) · leff2) / 8 + (Fsd · leff) / 5; (14) Мsd = ((0,297 + 4,31) · 2,882) / 8 + (1,5 · 2,88) / 5 = 5,64 кНм. Vsd = (( g1 + g2) · leff) / 2 + Fsd; (15) Vsd = (( 0,297 + 4,31) · 2,88) / 2 + 1,5 = 8,13 кН. Наиболее невыгодной по изгибающему моменту и поперечной силе является 1-ая комбинация нагрузок. Ребро армируется одним плоским каркасом. Рабочая арматура стержневая класса S500 (fyd = 435 МПа). Ширину полки тавра определяем по формуле: bf′ = bsb + 2 · bсвеса, (16) где bсвеса - ширина свеса, которая не должна превышать 1/6·leff = 1/6·2,88 = 0,48 м. В принятом ранее сечении bсвеса= (1,4 - 0,08) / 2 = 0,66 м > 0,48 м, поэтому в расчет принимаем bсвеса = 480 мм. bf′ = 80 + 2 · 480 = 1040 мм. Расчетную рабочую высоту сечения d определяем с учетом толщины защитного слоя и половины диаметра рабочей арматуры (принимая во внимание указания табл.11.4 [1, изм. 3], ориентировочно примем с = 30 мм): d = h – c =150 – 30 =120 мм. Предполагая, что нейтральная ось проходит по нижней грани полки, определяем область деформирования для прямоугольного сечения шириной bf′ = 1040 мм и положение нейтральной оси при расчете тавровых сечений:
Для арматуры S500 при Еs=2·105 МПа
Проверим выполнение условия:
Условие выполняется, т.е. нейтральная ось проходит в полке и расчетное сечение – прямоугольное с шириной bf′ =1040 мм.
Определяем значение коэффициента αm: αm = 6,52 · 103 / 1 · 20 · 10-3 · 1040 · 1202 = 0,022 < αm,lim = 0,371. Т.к. αm < αm,lim, то арматура в сечении используется полностью. Далее определяем значение коэффициента η:
Требуемая площадь растянутой арматуры: Ast = Msd / (fyd · η · d) = 6,52 · 106 / (435 · 0,989 · 120) = 126,29 мм2. Принимаем 1 Ø14 мм S500 площадью 153,9 мм2. Прочность железобетонных элементов на действие поперечных сил при отсутствии поперечной арматуры, согласно требованиям норм [1], проверяем по условию: Vsd ≤ VRd,ct, где Vsd – расчетная поперечная сила от внешних воздействий; VRd,ct – поперечная сила, воспринимаемая железобетонным элементом без поперечного армирования. Находим поперечную силу, воспринимаемую железобетонным элементом без поперечного армирования: Vrd,ct = (0,12 · k · (100 · ρ · fck)⅓ - 0,15 · σср) · bsb · d, (18) где
ρ – коэффициент армирования; ρ = Ast / (bw · d) ≤ 0,02; (20) ρ = 153,9 / (80 · 120) = 0,016 < 0,02; σср – напряжения в бетоне, вызванные наличием осевого усилия, σср = 0; Vrd,ct = (0,12 · 2 · (100 · 0,016 · 30)⅓ - 0,15 · 0) · 80 · 120 · 10-3 = 8,37 кН. Но не менее VRd,ct,min = (0,4 ∙ fctd - 0,15 ∙ σср) ∙ bw ∙ d, (21) VRd,ct,min = (0,4 ∙ 1,33) ∙ 0,08 ∙ 0,12 · 103 = 5,11 кН. Поскольку Vsd = 9,05 кН > VRd,ct = 8,37 кН, поперечную арматуру необходимо устанавливать по расчету. Проверяем условие обеспечения прочности по наклонной полосе между наклонными трещинами: VSd ≤ VRd,max, (22) где VRd,max должно быть в пределах: VRd,max = 0,3· ηw1 · ηc1 · ƒcd · bw ·d, (23) где ηw1 - коэффициент, учитывающий влияние поперечной арматуры, нормальной к продольной оси элемента, ηw1 = 1 + 5 · αE · ρsw ≤ 1,3, (24) αE - коэффициент перехода от арматуры к бетону; αE = Еs/ Еc; (25) где Еs - модуль упругости арматуры, Еs = 2·105 МПа; Еc - модуль упругости бетона, Еc = 36,9·103 МПа(см. п.2.1); αE = 2·105 / (36,9·103) = 5,42; ρsw - коэффициент армирования поперечной арматурой; ρsw = Asw / (bw · S); (26) Asw - площадь поперечной арматуры, пересекаемая наклонной полосой бетона; bw - минимальная ширина поперечного сечения элемента в растянутой зоне; ρsw = 28,3 / (80 · 150) = 0,0024. Подставляем найденные значения αE и ρsw в формулу (24): ηw1 = 1 + 5 · 5,42 · 0,0024 = 1,07 < 1,3; ηс1 = 1 - β4 · ƒcd; (27) β4 = 0,01- для тяжелых бетонов; ηс1 =1 - 0,01· 20 = 0,8. Проверяем условие (22), подставив найденные значения: VRd,max = 0,3· 1,07 · 0,8 · 20 · 80 ·120 = 49,31 кН. Vsd = 9,05 кН < VRd,max = 49,31 кН. Следовательно, диаметр хомутов и их шаг выбраны верно. Теперь необходимо произвести расчет поперечного ребра с поперечной арматурой по наклонной трещине. Вычисляем поперечную силу, которую могут воспринимать бетон и поперечная арматура:
где ηс2 = 2 - для тяжелых бетонов; ηf - коэффициент, учитывающий влияние сжатых полок в тавровых и двутавровых элементах: ηf = 0,75 · ( bf´ - bw) · hf´ / ( bw · d) ≤ 0,5; (29) причем должно выполняться условие: bf - bw ≤ 3 · hf´; (30) bf - bw = 1040 – 80 = 960 > 3 · hf´ = 3 · 40 = 120. Условие не выполняется, поэтому вместо ( bf´ - bw) вводим в расчет 3· hf = 120 мм. ηf = 0,75 · 120 · 40 / (80 · 120) = 0,375 ≤ 0,5; ηN - коэффициент, учитывающий влияние продольных сил, ηN =0. Находим линейное усилие, которое может воспринять поперечная арматура: Vsw = asw · nw · fywd / Sw , (31) где asw - площадь поперечного сечения стержня Ø 6 мм; nw - количество пересекаемых наклонной полосой бетона стержней поперечной арматуры; fywd = 174 МПа – расчетное сопротивление поперечной арматуры [1,изм.4, таб.6.5]; Sw - шаг хомутов; Vsw = 28,3 · 1 ·174 / 150 = 32,83 Н/мм. Подставляя найденные значения в формулу (28), находим значение Vrd:
Поперечная сила, которую могут воспринять хомуты и бетон Vsd = 9,05 кН < Vrd = 23,55 кН, следовательно, прочность наклонных сечений обеспечена. Среднее поперечное ребро высотой 250 мм рассчитывается аналогично. Постоянная расчетная нагрузка на ребро: - от собственного веса ребра (без учета полки) g1 = 0,08 · 0,21 · 2500 · 10 · 1 · 1,35 = 567 Н/м =0,567 кН/м; - передаваемая полкой плиты g2 = 3,079 · 1,4 = 4,31 кН/м; - расчетная снеговая нагрузка на ребро gsd = 1,2 · 1,4 = 1,68 кН/м. Расчетный изгибающий момент в пролете: Мsd = ((g1 + g2 + gsd) · leff2) / 8 = ((0,567 + 4,31 + 1,68) · 2,882)/8 = 6,8 кНм. Поперечная сила у опор: Vsd = (( g1 + g2 + gsd) · leff) / 2 = ((0,567 + 4,31 + 1,68) · 2,88) / 2 = 9,44 кН. Расчетные усилия в ребре от постоянной нагрузки и сосредоточенной от веса рабочего с инструментом Fsd =1·1,5 = 1,5 кН Мsd = ((g1+g2)·leff2)/8+(Fsd·leff)/5=((0,567+4,31)·2,882)/8+(1,5·2,88)/5 = = 5,92 кНм. Vsd = (( g1+g2)·leff)/2+Fsd = (( 0,567+4,31)·2,88)/2+1,5 = 8,52 кН. Наиболее невыгодной по изгибающему моменту и поперечной силе является 1-ая комбинация нагрузок. Ребро армируется одним плоским каркасом. Рабочая арматура стержневая класса S500 (fyd = 435 МПа). Определяем ширину полки. В принятом ранее сечении bсвеса = (1,4 - 0,08) / 2 = 0,66 м > 1/6 · leff = 1 / 6 · 2,88 = 0,48 м, поэтому в расчет принимаем bсвеса = 480 мм. bf′ = 80 + 2 · 480 =1040 мм. Рабочая высота сечения: d = h – c = 250 – 30 = 220 мм. Предполагая, что нейтральная ось проходит по нижней грани полки, определяем область деформирования для прямоугольного сечения шириной bf′ =1040 мм и положение нейтральной оси при расчете тавровых сечений:
Проверим выполнение условия:
Условие выполняется, т.е. нейтральная ось проходит в полке и расчетное сечение – прямоугольное с шириной bf′ = 1040 мм. Тогда
Определяем значение коэффициента αm: αm = 6,8 · 103 / 1 · 20 · 10-3 · 1040 · 2202 = 0,007 < αm,lim = 0,371. Т.к. αm < αm,lim, то арматура в сечении используется полностью. Далее определяем значение коэффициента η:
Требуемая площадь растянутой арматуры: Ast = Msd / (fyd · η·d) = 6,8 ·106 / (435 · 0,996 · 220) = 71,34 мм2. Принимаем 1 Ø10 мм S500 площадью 78,5 мм2. Прочность железобетонных элементов на действие поперечных сил при отсутствии поперечной арматуры, согласно требованиям норм [1], проверяем по условию: Vsd ≤ VRd,ct. Находим поперечную силу, воспринимаемую железобетонным элементом без поперечного армирования:
ρ = As t/ (bw · d) ≤ 0,02 = 78,5 / (80 · 220) = 0,004 < 0,02. Vrd,ct = (0,12·k·(100·ρ·fck)⅓-0,15·σср)·bsb·d = (0,12·2·(100·0,004·30)⅓- -0,15·0)·80·220·10-3 = 9,67 кН. Но не менее VRd,ct,min=(0,4∙fctd-0,15∙σср)∙bw∙d=(0,4∙1,33)∙0,08∙0,22·103= 9,36 кН. Поскольку Vsd = 9,44 кН < VRd,ct=9,67 кН, поперечная арматура устанавливается конструктивно. Принимаем с учетом технологии точечной сварки поперечную арматуру из проволоки Ø6 S240 с шагом 150 мм.
Расчет продольного ребра 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
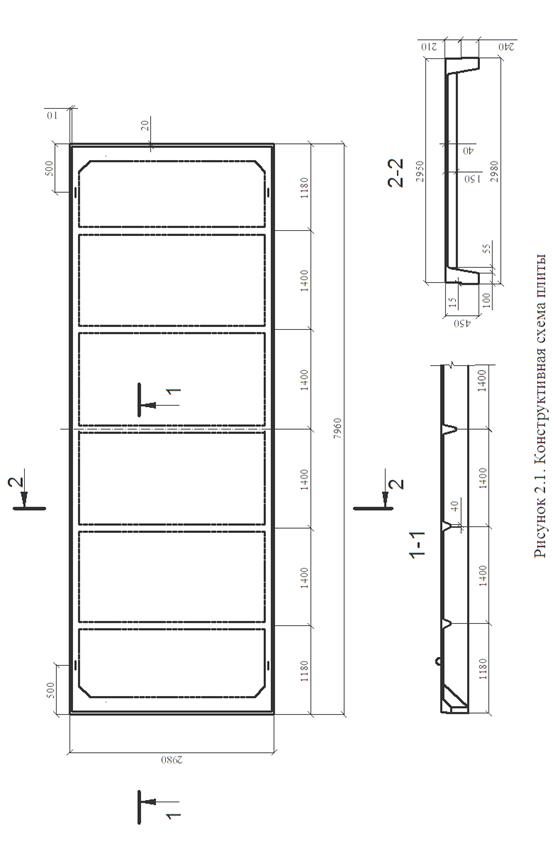
 l2 = 2980 – 2 × 155 = 2670 мм.
l2 = 2980 – 2 × 155 = 2670 мм.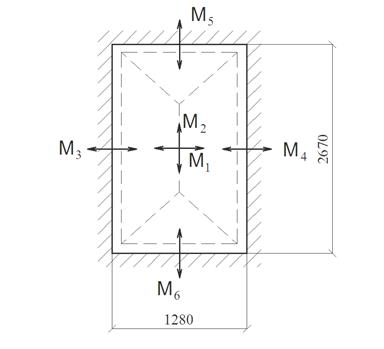
 ; (10)
; (10)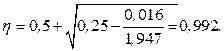
 ≥ 0,13;
≥ 0,13; > 0,13.
> 0,13.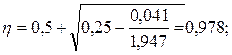
 (17)
(17)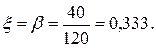
 ‰
‰ что указывает на то, что сечение находится в области деформирования 2 [5, таб.6.7] , для которой
что указывает на то, что сечение находится в области деформирования 2 [5, таб.6.7] , для которой  .
.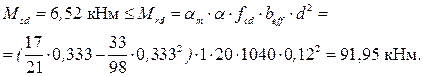
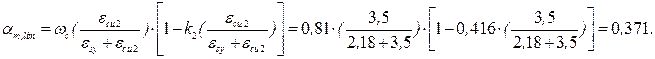
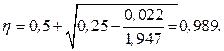
 ; (19)
; (19) ; принимаем k = 2;
; принимаем k = 2;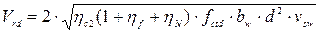 , (28)
, (28) =23,55 кН.
=23,55 кН.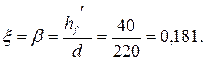
 что указывает на то, что сечение находится в области деформирования 1b [5, таб.6.7], для которой
что указывает на то, что сечение находится в области деформирования 1b [5, таб.6.7], для которой  .
.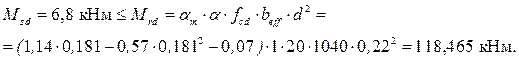
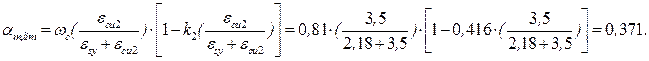
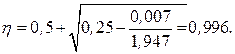
 ; принимаем k=1,95;
; принимаем k=1,95;