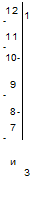КРИТЕРИИ И ШКАЛА ОЦЕНИВАНИЯ

контрольных заданий

Выполнение заданий текущего контроля оценивается по единой схеме, основанной на вычислении коэффициента результативности (КР) учебных достижений по дисциплине «Управление инвестиционным портфелем». Для этого:

· подсчитывается количество правильных ответов к заданиям теста для текущего контроля (А), при этом каждое тестовое задание оценивается в бинарной шкале «правильно-неправильно»;

· фиксируется максимальное количество баллов за правильные ответы к заданиям для данного теста (Аmax=20 баллов).

Величина коэффициента результативности учебных достижений студентов в рамках текущего контроля вычисляется по следующей формуле: КР= А / Аmax.

Значения КЗ изменяются в пределах от 0 до 1. Баллы в балльно-рейтинговой системе Университета в зависимости от коэффициента результативности по итогам текущего контроля представлены в следующей таблице:

Коэффициент результативности (КР) выполнения контрольных заданий	0,8< КР ≤1	0,6≤ КР ≤0,8	0,4≤ КР <0,6	0≤ КР <0,4
Баллы в БРС Университета за КЗ №1 «Налоговая политика Российской Федерации: цели, задачи, основные направления»	15 баллов	12 баллов	10 баллов	0 баллов
Баллы в БРС Университета за КЗ №2 «Особенности исчисления и уплаты налогов»	15 баллов	12 баллов	10 баллов	0 баллов

Ключи ответов

к контрольным заданиям по учебному предмету «Управление инвестиционным портфелем»

Номер вопроса	Варианты ответов
	c
	d
	b, c
	c
	c
	a
	b
	a, c
	a
	b
	b, c
	b, d
	a
	d
	a
	a, b, d
	b
	a
	a
	a, d
	b
	a
	a, b
	b
	c
	c, d
	b
	a
	d
	d

Бланк ответов

к вариантам заданий для текущего контроля

по дисциплине «Управление инвестиционным портфелем»

Номер вопроса	Варианты ответов

Негосударственное образовательное учреждение

Высшего профессионального образования

«Санкт-Петербургский университет управления и экономики»

ИНСТИТУТ Международных программ

Кафедра международных финансов и бухгалтерского учета

кейс-задание

по дисциплине

Управление инвестиционным портфелем

Составитель _________________________________

^{(подпись)}

«___» ________________________________ 2015 г.

Кейс-задание(раздел «Теория выбора портфеля»):

Для двух видов ценных бумаг известны следующие данные:

Ценная бумага	Ожидаемая доходность ц,	Стандартное отклонение
	%	доходности и, %
Высокий риск
Низкий доход

Доходности обоих ценных бумаг положительно коррелируют, коэффициент корреляции составляет р = 60%.

1. Рассчитайте ожидаемую доходность и стандартное отклонение портфеля, который на 70% состоит из бумаг фирмы «Высокий риск» и на 30% — из бумаг фирмы «Низкий доход».

2. Определите множество эффективных портфелей, рассчитывая ожидаемую доходность и риск в форме стандартного отклонения при различных изменениях доли ценных бумаг каждого вида в портфеле. Постройте график эффективного множества портфелей.

3. Какую ожидаемую доходность имеет безрисковый портфель, если коэффициент корреляции доходности обоих ценных бумаг составляет не 60%, а существенно близок к —1?

Критерии и шкала

оценивания кейс- задания

(max 20 баллов)

Критерии и шкала оценивания кейс-задания(max 20 баллов)

1) сформулировано и проанализировано большинство проблем, заложенных в кейсе; 2) продемонстрированы адекватные аналитические методы при работе с информацией; 3) использованы дополнительные источники информации для решения кейса; 4) выполнены все необходимые расчеты, сделаны обоснованные выводы, которые отличают данное решение кейса от других решений.

Каждый из предложенных критериев оценивается по шкале «выполнен-выполнен частично-не выполнен», что соответствует следующему распределению баллов «5 балла- 3 балл-0 баллов»

Баллы за выполнение кейс-задания определяются в БРС Университета как сумма набранных баллов по совокупности всех предложенных для его оценивания критериев.

Решение кейс-задания:

к 1:

Для ожидаемой доходности портфеля из двух видов ценных бумаг верна следующая формула:

ц_р =<7ixpj +?₂ХМ.₂>

где q_v q₂ — доли отдельных ценных бумаг в портфеле, причем q_{ + q₂ = 1.

При заданной ожидаемой доходности обоих ценных бумаг получаем:

Цр =0,7х11% + 0,Зх9% = 7,7% + 2,7% = 10,4%.

При расчете стандартного отклонения портфеля из двух видов ценных бумаг наряду со стандартными отклонениями отдельных видов ценных бумаг также учитывается коэффициент корреляции доходности ценных бумаг обоих видов. Получается следующая формула:

Стр = хо? + ?2 ^xal + 2х<7! xctj xq₂ ха₂р.

При подстановке заданных величин получается:

Стр = л/о,7² х25%² + 0,3² х19%² + 2 х0,7 х25% х0,3 х19% х60%,

Ор = д/0,030625 + 0,003249 +0,01197 = ,/0,045844 =21,4%.

к 2:

Доля акций «Высокий риск» qi	Доля акций «Низкий доход»q₂	Ожидаемая доходность портфеля, %	Стандартное отклонение портфеля, %
0,0	1,0	9,0	19,0
0,1	0,9	9,2	18,7
0,2	0,8	9,4	18,6
0,3	0,7	9,6	18,8
0,4	0,6	9,8	19,2
0,5	0,5	10,0	19,7
0,6	0,4	10,2	20,5
0,7	0,3	10,4	21,4
0,8	0,2	10,6	22,5
0,9	0,1	10,8	23,7
1,0	0,0	11,0	25,0

Эффективные портфели обладают тем свойством, что не существует другого портфеля с той же самой ожидаемой доходностью и меньшим стандартным отклонением или соответственно с одинаковым стандартным отклонением и более высокой ожидаемой доходностью.

При инвестиции только в ценные бумаги фирмы «Низкий доход» или, соответственно, при доле этих бумаг в портфеле, равной 90%, существуют такие портфели, которые при одинаковом стандартном отклонении позволяют достичь более высокой ожидаемой доходности. Поэтому оба указанных портфеля не принадлежат множеству эффективных портфелей.

Эта эффективная граница множества допустимых портфелей возникает, поскольку все эффективные портфели располагаются на одной кривой (см. рисунок).

кЗ:

Полностью отрицательная корреляция означает, что коэффициент корреляции доходности обоих ценных бумаг точно равен р = -1. В этом случае для стандартного отклонения портфеля, состоящего из двух видов финансовых титулов, верно следующее соотношение:

а_р =_Л/<?₁² хо² + q₂ ха² -2x0j хо, xq₂xo₂;

о_р = ^xoi -92XO2)²; o_p=q_{ XCT_t -?₂xo₂.

При условии, что q₂ = 1 - ft, отсюда следует, что = ft х Oj - (1 - ft ) х сг₂.

Чтобы сформировать безрисковый портфель, нужно положить о_р = 0 .

Если a_t =25% , то получим 0 = ft x25%-(l-ft )х19%.

Отсюда легко получить, что ft =43,2% и q₂ =56,8%.

Доходность портфеля с нулевым риском при этом составит:

[i_p =0,432x11%+ 0,568x9% = 9,9%

В случае, когда доходности ценных бумаг обоих видов полностью отрицательно коррелируют друг с другом, риск портфеля из двух видов финансовых титулов при определенном их соотношении можно полностью исключить. В нашем примере доходность этого портфеля с нулевым риском составляет 9,9%

123

Не нашли, что искали? Воспользуйтесь поиском по сайту: