|
|
Смежные классы. Теорема Лагранжа.12 Определение 1: Говорят, что элементы а, b группы G сравнимы по подгруппе H справа (слева), и пишут а = b(Н)п (а = b(H)л) , если ab-1 ∊ H (а-1b ∊ H). Если G — абелева группа, то отношения сравнимости по H справа и слева совпадают. Определение 2: Правым (левым) смежным классом группы (G, •) по ее подгруппе H с представителем g ∊ G называется множество Hg (множество gH). Теорема 1: Пусть Н — подгруппа группы (G, •) Тогда: а) отношение сравнимости на G по подгруппе Н справа есть отношение эквивалентности; б) для любого g ∊ G класс элементов, сравнимых с g пo H справа, есть Hg. Любые два правых смежных класса группы G по подгруппе Н либо не пересекаются, либо совпадают. Группа G распадается на непересекающиеся правые смежные классы по подгруппе Н. Аналогичные утверждения верны для левых смежных классов группы G по подгруппе Н и отношения сравнимости по Н слева. Доказательство: а) Обозначим, для краткости, отношение сравнимости на G по Н справа через р, т. е. положим Va, b ∊ G: apb <=> а = b(Н)п <=> ab-1 ∊ H. Отношение р — рефлексивно, так как е ∊ H, и симметрично, так как в Н существует обратный для каждого элемента из H. Наконец, р — транзитивно, так как если apb и bрс, то аb-1 ∊ H, bc-1 ∊ H , и потому ac-1 = (ab-1) • (bc-1) ∊ H, т. е. aрc. . б) Для каждого g ∊ H класс Теорема 2: а) Любые два правых (левых) смежных класса группы G по подгруппе H равномощны. В частности, в конечной группе G для любого g ∊ G верны равенства |Н| = |Нg| = |gН|. б) Множество υ правых смежных классов G по Н равномощно множеству £ левых смежных классов G по Н. Доказательство: а) Достаточно заметить, что отображение φ: H—>Hg , определяемое формулой Vh ∊ H (φ(h) = hg) ,есть биекция. Следовательно, все смежные классы G по H равномощны H. б) Для любых g1,g2 ∊ G справедливы импликации: H Отсюда следует, что отображение ψ: υ—> £ определяемое условием VHg ∊ υ: ψ(Нg) =g-1H, задано корректно и инъективно. Его сюрьективность очевидна. Таким образом, ψ— биекция. Определение 2: Индексом подгруппы Н в группе G называют число правых (левых) смежных классов G по H, если это число конечно, и бесконечность — в противном случае. Индекс H в G обозначают через |G : Н|. Очевидно, что если H < G, то H = G ó |G : Н| = 1. Теорема Лагранжа: Порядок подгруппы H конечной группы G делит порядок G и |G| = |G : Н| • |H|. Доказательство: Разложение G на правые смежные классы по подгруппе H имеет вид G = H
Вопрос18: Разложение подстановки в произведение независимых циклов. Цикловая структура подстановки. Каждая подстановка g ∊ S(Ω) задается таблицей G = Означающей , что подстановка g отображает число k в g = (a1,a2,…,ar)(b1,b2,…,bs)(с1,с2,…,сt). Определение 1: Если в цикловой записи подстановки g ∊ Теорема 1: Любая подстановка g из группы
Вопрос 19: 
12 Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
всех элементов, р — эквивалентных g, имеет вид 
и Нg2 = 
либо не пересекаются, либо совпадают, и если {Н 
: α ∊ А} — множество всех различных правых смежных классов G по H, то G = 
.
= H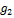 
óg1g2-1 ∊ H ó (g1-1)-1g2-1 ∊ H ó g1-1H = g2-1H.
, где k = |G : H|. Отсюда |G| = |H 
,
, k = 1,…,n.Существует и другая форма записи подстановок, когда образ элемента k записывается не под ним , а справа от него. Приведем алгоритм получения такой записи подстановки g ∊ 
. Запишем сначала любое число а1 
Ω, за ним через запятую запишем его образ при действии подстановки g, т.е. число а2 = g(а1), затем число а3 = g(а2) и т.д. до тех пор , пока не появиться число 
такое, что g( 
при I ≤ r.Такой момент обязательно наступит в силу конечности множества Ω.Теперь набор чисел а1,а2,…,аr заключаем в скобки и называем циклом длины r подстановки g.Если множество Ω не исчерпано, то выбираем в нем любой из оставшихся элементов b1 и аналогичным образом строим цикл (b1,b2,…,bs). Продолжая этот процесс до исчерпания всех элементов множества Ω, мы получим так называемую цикловую запись подстановки g: