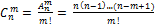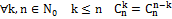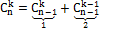|
|
Сочетания, размещения, перестановки. Теоремы о числе сочетаний, размещений и перестановок, их следствия.12 Методы математических доказательств (метод непосредственной проверки, метод доказательства от противного, метод математической индукции). 1)Метод непосредственной проверки: Этим методом обычно доказывают равенства или некоторые другие соотношения, а само доказательство заключается в осуществлении последовательности действий, существо и порядок которых определяются самой формулировкой доказываемого утверждения. 2) Метод доказательства от противного: Для доказательства этим методом некоторого утверждения А допускают, что утверждение А ложно, то есть истинно его отрицание A*. Далее, с использованием утверждения А* доказывают некоторое заведомо ложное утверждение F и из этого делают вывод о том, что сделанное предположение о ложности А неверно, и поэтому А — истинно. В основе этого метода лежит логическое правило (А* => F, F == л) => А. 3) Метод полной математической индукции: Этот метод применяют для доказательства таких утверждений, в формулировке которых участвует числовой параметр n, принимающий все значения из множества N натуральных чисел. Процесс доказательства методом полной математической индукции состоит из двух этапов. А) Доказывают, что утверждение A(t) истинно при t = 1 (это чаще всего удается сделать непосредственной проверкой). Б) Исходя из допущения, что утверждение A(t) верно для произвольного фиксированного значения t = n доказывают его истинность при t = n + 1.
1 МЕТОД. Теорема: Модуль смешанного произведения численно равен объёму параллелепипеда, построенного на векторах Доказательство:
Доказано. 2 МЕТОД. Докажем одно из следствий аксиом линейного пространства. Например: Единственность ноль вектора. Допустим, что есть 2 ноль вектора По определению: 1) 2) Положим:
Предположение оказалось неверным => ноль вектор единственен Доказано. 3 МЕТОД. Доказать методом математической индукции, что Доказательство: 1) Проверяем верность данной формулы при n=1. Левая часть = 1. Правая часть 2) Предполагая, что данная ф-ия верна для некоторого n>1, докажем что при n+1 имеет место такая же формула: Действительно:
ч.т.д. Делаем вывод на основании математической индукции, что формула верна для
Вопрос 2. Формула Бинома Ньютона. Для любого натурального числа n справедлива формула:
Доказательство: Метод математической индукции. 1) Проверяем верность формулы при n=1:
2) Предполагая, что формула верна для некоторого n, покажем, что она верна для n+1 т.е. докажем справедливость формулы:
Действительно, используя сначала свойства степени с натуральным показателем, далее исходную формулу Бинома Ньютона и правило перемножения многочленов получим:
Приводя подобные члены имеем:
откуда в силу того, что
Из 1) и 2) на основании метода математической индукции заключаем, что формула верна Теорема Доказана. Следствия: 1)Число всех членов разложения на единицу больше показателя Бинома. Это видно из самой формулы. 2)Сумма показателей степени при a и b в любом слагаемом разложения равна n – показателю степени Бинома. 3)Биномиальные коэффициенты, равноудалённые от концов разложения равны между собой, т.к. 4) Общий член разложения имеет вид:
Положив k=0,1,2…n получаем первый, второй и другие члены разложения. Например 5)Сумма всех биномиальных коэффициентов равна Действительно, полагая a=b=1 получим:
6)Число всех подмножеств n-элементного множества равно Также формула имеет вид
Вопрос 3. Сочетания, размещения, перестановки. Теоремы о числе сочетаний, размещений и перестановок, их следствия.
Определение 1: Размещением из n элементов множества А = {a1,...,an} по m называется любой упорядоченный набор m различных элементов множества А. Определение 2: Любой упорядоченный набор всех n элементов множества A, взятых по одному разу, называется перестановкой элементов множества А. Определение 3: Сочетанием из n элементов множества А = {a1,...,an} пo m называется любое m-элементное подмножество множества А. Теорема: Введем следующие обозначения:
Сочетаний Размещение Перестановки Pn= n! Доказательство: Укажем путь построения всех размещений по m элементов из множества |А|=n .Каждое такое размещение имеет вид: (a1,а2,…..,аm),где а1,а2,…,аm – различные числа из А. При построении размещения в качестве а1 можно взять любое число из множества А.Следовательно, число различных вариантов выбора а1 равно n.Если первый элемент размещения уже выбран, то в качестве 2-ого можно взять любое число, отличное от первого. Следовательно, при любом первом элементе второй можно выбрать в n-1 вариантах. Значит, указанным образом упорядоченных пар вида а1,а2 можно построить n(n-1) штук. Аналогично, при любых выбранных а1,а2 в качестве а3 можно взять любое из n-2 оставшихся чисел. Следовательно, упорядоченных троек вида а1,а2,а3 можно составить n(n-1)(n-2). Продолжая этот процесс, мы построим n(n-1)…(n-m+1) размещений. Легко видеть, что все построенные размещения различны и любое размещение из n по m будет таким образом построено. Формула для перестановок получается в частном случае, когда m=n. Докажем формулу для сочетаний. Возьмем произвольное сочетание (а1,а2,…аm). Переставляя всевозможным образом его элементы, мы получим формулу
Доказано.
Следствие 1:
Следствие 2:
Вопрос 4. 
12 Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
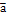 ,
, 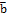 ,
,  .
.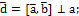
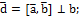
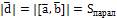
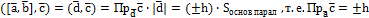

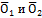 .
.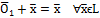



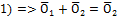
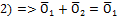 =>
=> 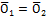

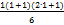 =1. Значит формула верна для n=1.
=1. Значит формула верна для n=1.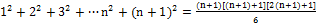 .
.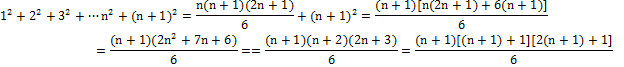
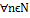 .
.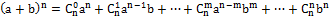 – формула Бинома Ньютона.
– формула Бинома Ньютона.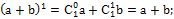
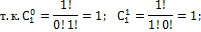

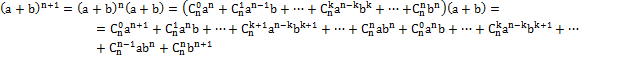
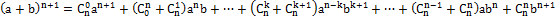 ,
,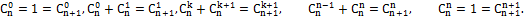

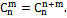
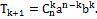
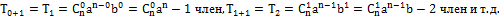
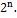
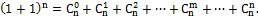
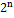 .
.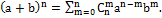
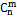 -- число различных сочетаний из n no m,
-- число различных сочетаний из n no m, – число различных размещений из n по m.
– число различных размещений из n по m. Верны формулы:
Верны формулы: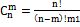 =
= 
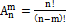 = n(n-1)…(n-m+1)
= n(n-1)…(n-m+1)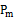 = m!. Следовательно, мы получили m! различных размещений из n по m. Отсюда видно, что число различных размещений из n по m в m! Раз больше числа сочетаний из n по m. Следовательно,
= m!. Следовательно, мы получили m! различных размещений из n по m. Отсюда видно, что число различных размещений из n по m в m! Раз больше числа сочетаний из n по m. Следовательно,