
|
|
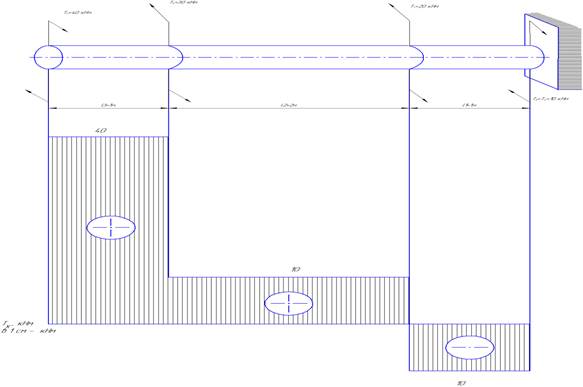
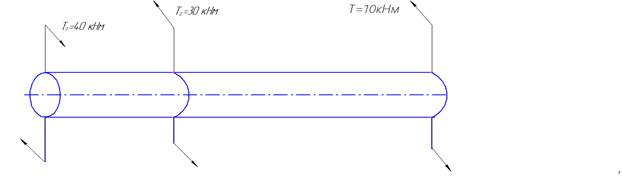
Внутренние усилия при кручении стержня12 Крутящим моментом в поперечном сечении стержня называется проекция главного момента системы внутренних сил на ось x. Рассмотрим прямолинейный стержень, нагруженный внешними парами сил, лежащими в плоскостях, перпендикулярных оси стержня. Моменты таких пар называются скручивающими моментами. Чтобы определить крутящие моменты в поперечных сечениях стержня и построить эпюру крутящих моментов, заменим пары сил M векторами их моментов. Как известно, вектор момента пары сил перпендикулярен плоскости действия пары сил и направлен в ту сторону, откуда вращение пары кажется происходящим против часовой стрелки
Поскольку скручивающие пары сил расположены в плоскостях, перпендикулярных оси стержня, следовательно, векторы моментов этих пар будут направлены по оси стержня. Определим крутящие моменты Т. в каждом сечении. Сечение 1-1: рассматриваем левую часть стержня. 0≤
Составляем уравнение равновесия для рассматриваемой части стержня
Поскольку величина T не зависит от координаты сечения 1-1, следовательно, на первом участке крутящий момент постоянен и равен
Находим крутящие моменты на остальных участках. 1≤
3≤
Координаты потенциально опасных сечений находятся на первом участке:
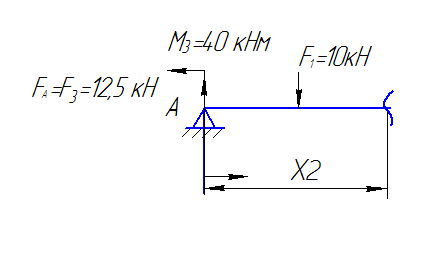
Внутренние усилия при изгибе консольной балки с жесткой заделкой Поперечной силой в сечении называется проекция главного век Рассмотрим прямолинейный стержень, подверженный плоскому поперечному изгибу Требуется определить внутренние силы в поперечных сечениях стержня и построить эпюры внутренних силовых факторов. Составляем уравнение равновесия для системы сил, действующих на рассматриваемую часть стержня, что бы найти опорную реакцию FA и момент MA
Делаем проверку на правильность расчетов FA и MA :
10-20+10 Проверка не обнаруживает ошибок в определении FA , MA.
Проведем сечение на первом грузовом участке и рассмотрим левую часть стержня 0≤
Функция QY (х) есть производная от М(х) и на границах участка меняет знак, следовательно, внутри промежутка [0;2] она обращается в ноль, а функция М(х) в этой точке имеет экстремум. Находим координату точки экстремума: Qy1=0
Определяем значение Mz1 в произвольной точке участка:
х=0,5 Проведём сечение на втором грузовом участке и рассмотрим правую часть стержня: 1м≥
Координата потенциально опасных сечений, как видно из эпюры Qx в начале первого участка при и на протяжении всего второго участка, где Qx постоянно и также равно и, как видно из эпюры Мz,
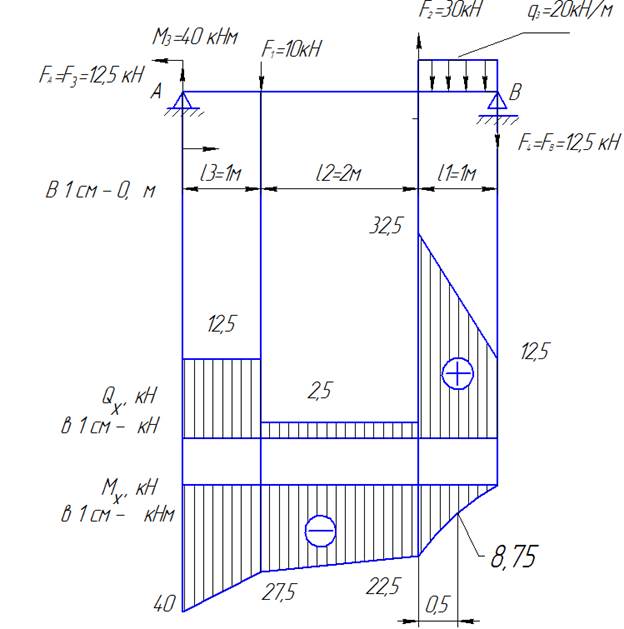
Внутренние усилия при изгибе балки на двух шарнирных опорах с одной консолью
Требуется определить внутренние силы в поперечных сечениях стержня и построить эпюры внутренних силовых факторов. Определим опорные реакции FA и FВ, составив 2 уравнения равновесия
Проверка
-10+30+12,5-20-12,5=0 - силы рассчитаны верно
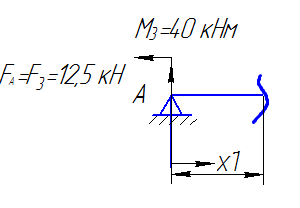
Проведем сечение на первом грузовом участке и рассмотрим левую часть стержня 0≤
Составляем 2 уравнения равновесия для системы сил, действующих на рассматриваемую часть стержня.
Рассмотрим сечение на втором грузовом участке и рассмотрим левую часть стержня 1м≤
Проведем сечение на третьем грузовом участке и рассмотрим правую часть стержня:
Найдём значение 0<х<1 х=0,5
Потенциально опасное сечение, как видно из эпюры Qx находится на третьем грузовом участке при хi=1м, где
Заключение Контроль правильности построения эпюры Nx В сечении, где приложена сосредоточенная сила Fi, на эпюре Nx должен быть скачок, численно равный этой силе и направленный вверх, если сила Fi растягивающая, т.е. положительна, и вниз, если сила Fi сжимающая, то есть отрицательна.
Контроль правильности построения эпюры Тx В сечении, где приложен скручивающий момент Тi на эпюре Тx должен быть скачок, численно равный этому моменту, и направленный вверх, если момент Ti положителен, и вниз, если момент Ti отрицателен.
Дифференциальные зависимости при изгибе Предлагаемый метод расчета параметров Qx и Мxпозволяет не выводить, a просто констатировать дифференциальные зависимости при изгибе. Для силы Qxi и для момента Мxi непосредственно следует: производная от изгибающего момента Мxi по координата хi равна поперечной силе Qxi, то есть
Для силы Qxi следует: производная от поперечной силы по координате xi равна распределенной нагрузке qi на грузовом участке, то есть
Из выражений (4.1) и (4.2) следует
Как видим, вторая производная от изгибающего момента Мxi по координате хi равна распределенной нагрузке qi на грузовом участке. Зависимости (4.1) и (4.2) позволяют выявлять ошибки при составлении уравнений для параметров Qxi и Мxi еще до выполнения численных расчетов и до построения эпюр Qx и Мx. Все выше приведенные правила контроля правильности построения эпюр использовались при выполнение работы и не выявили ошибок в построении эпюр. 
12 Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 ≤1м
≤1м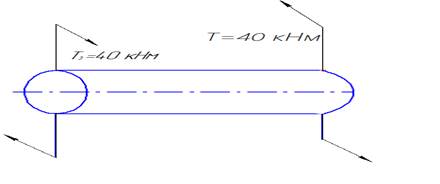
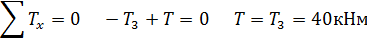
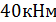 .
.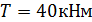
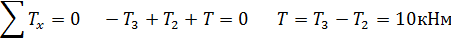

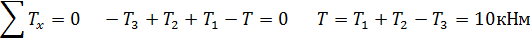
 кНм
кНм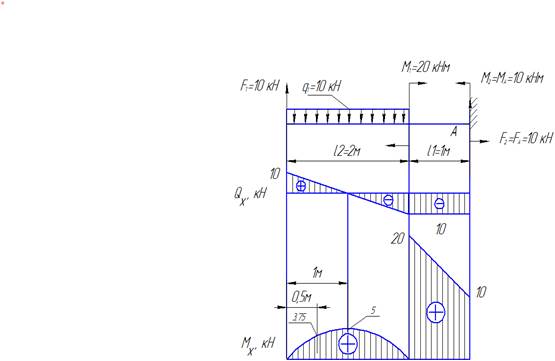
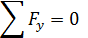
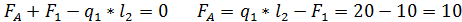


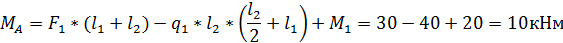

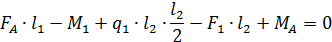
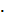 2
2 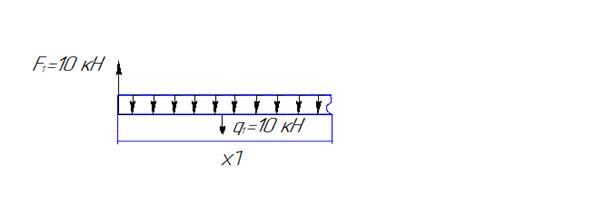
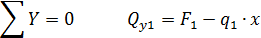
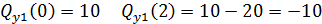
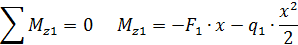
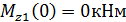
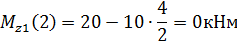
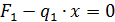 х=1
х=1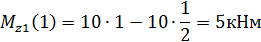
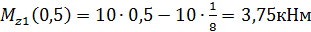
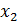 ≥0м
≥0м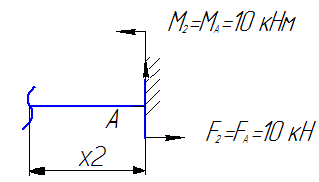
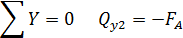
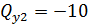
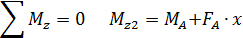
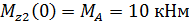
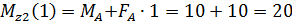 кНм
кНм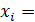 0м, где
0м, где 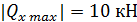 ;
;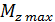 находится в конце второго участка при xi=1м
находится в конце второго участка при xi=1м  где |
где | 
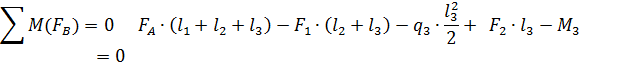
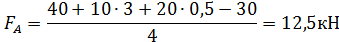
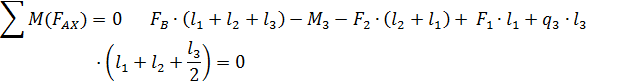
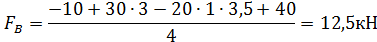
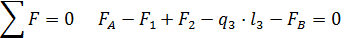
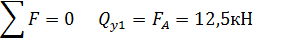
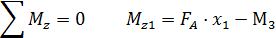

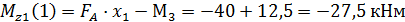
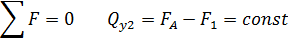
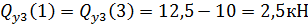
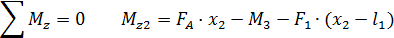
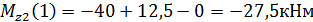
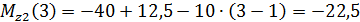 кНм
кНм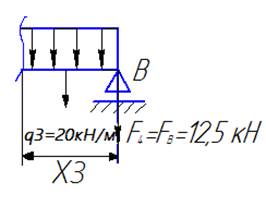
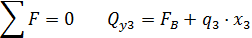

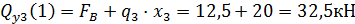
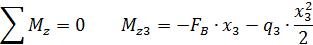
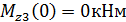
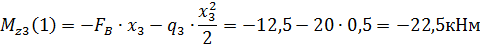
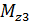 в произвольной точке на участке:
в произвольной точке на участке: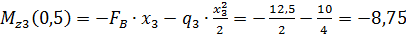
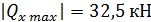 ; и, как видно из эпюры Мx, - на втором участке при xi=0м где
; и, как видно из эпюры Мx, - на втором участке при xi=0м где 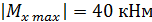 .
. (4.1)
(4.1) (4.2)
(4.2)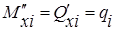 (4.3)
(4.3)