
|
|
Конструирование и расчет стержня колонны
5.1.1 Исходные данные Требуется подобрать сечения сплошной верхней и сквозной нижней части колонны. Расчетные усилия, согласно таблице РСУ: - для верхней части колонны (в узле 8): М= 121,381 кН·м; N= -130,851 кН; - для нижней части колонны М1= -418,838 кН·м; N= -334,18 кН - момент догружает подкрановую ветвь; М2= 255,93кН·м; N= -737,507 кН - момент догружает шатровую ветвь. Максимальное значение поперечной силы Qmax=47,934 кН. Соотношение жесткостей верхней и нижней части колонны: J2/J1 =0,072. Материал колонны: сталь С235 по ГОСТ 27772-88, Ry=230 МПа при t = 2…20 мм и для листа и для фасона.
Расчетные длины колонны Расчетные длины колонны определяем в соответствии с положением 6 [2] учитывая, что в нашем случае верхний конец колонны закреплен только от поворота. При этом, поскольку l2/ l1=H2/ H1=4,63/10,17=0.455<0.6, то можно использовать данные таблицы 18 [2].
Таким образом, расчетные длины в плоскости рамы будут: - для нижней части колонны: lefx1= μ1·H1=20,34 м; - для нижней части колонны: lefx2= μ2·H2=13,89м. Расчетные длины из плоскости рамы нижней и верхней частей колонны соответственно равны: lefу1= H1= 10,17 м; lefу2= H2 – hcb=3,78 м, где: hcb= 0,85 м – высота подкрановой балки.
Подбор сечения верхней части колонны Сечение верхней части колонны принимаем в виде сварного двутавра с высотой сечения h2=450 мм. Требуемую площадь сечения определяем, используя формулу Ясинского: σ= N/(φx·A)+Mx/Wx≤Ry·γc. Полагая φx≈0,8; Wx/А= ρ≈0,35·h2 – среднее значения, получим: Аr≥(N/ Ry·γc)(1.25+2.86·ex/ h2)=(130,85/23·1)·(1.25+2.86·92,8/45)=40,66 см2, где ex=М/ N =12138/130,85=92,8 см.
Компонуем сечение с учетом ограничений условиями местной устойчивости. Поскольку относительный эксцентриситет mx= ex/ ρ=92,8/15,75= 5,9 где: ρ=0,35·h2 =0,35·45=15,75 см – ядровое расстояние, и то согласно табл.27* [2] λuw=1.2+0.35 На этапе компоновки используем условие предельного отношения расчетной высоты стенки к ее толщине согласно п.7.14*[2] в форме:
Правая часть условия:
Тогда, принимая толщину полок tf=8 мм, будем иметь высоту стенки hw= h2 - 2tf=43,4 см. Толщина стенки определяется из вышеприведенного условия:
Принимаем На один пояс будет приходиться:
При tf=6мм, ширина полки составит:
Ширина полки, согласно должна быть в пределах
При найденных параметрах Предельное же согласно табл. 29* [2] отношение ширины полки к ее толщине:
Принимаем: h2 =45 см; hw =43,4 см; tw =0,6 см; bf =16 см; tf = 0,8 см. При этом фактическая площадь сечения верхней части колонны ,что обусловлено принятием конструктивных размеров элементов сечения.
Геометрические характеристики сечения:
По табл. 73 [2] коэффициент формы сечения: Приведенный относительный эксцентриситет: По таблице 74[2] φе = 0,1558.
Проверка устойчивости верхней части колонны в плоскости действия момента примет вид:
Поскольку недонапряжение составляет
Рисунок 18 - Поперечное сечение надкрановой части колонны
Проверка устойчивости из плоскости действия момента: Для определения mx , найдем максимальный момент в пределах средней трети расчетной длины верхнего участка колонны (см. рис.19).
Рисунок 19 Расчетная схема для определения максимального момента
При этом
Поэтому согласно п.5.31 [2]:
При полученных данных
Тогда:
Проверим местную устойчивость стенки согласно п.7.16*[2]. Наибольшее сжимающее напряжение у расчетной границы стенки
Соответствующее напряжение у противоположной кромки
Значение σ принимается со знаком “+” – см. п.7.16[2]
в связи с чем, проверку местной устойчивости стенки выполняем в соответствии с п.7.14*[2]. Согласно указанному пункту, отношение расчетной высоты стенки к ее толщине должно подчиняться условию:
В соответствии с таблицей 27*[2], при значении относительного эксцентриситета m>1 для двутаврового сечения при условной гибкости элемента в плоскости действия момента
Принимаем
Таким образом, условие примет вид 62<62,84(+1,3%<5%). Следовательно, местная устойчивость стенки обеспечена. Сечение верхней части колонны показано на рис.18. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|


 1=1.2+0.35 ·2,45= 2,06.
1=1.2+0.35 ·2,45= 2,06.




 Т.к требуемая площадь полки мала, то ширину полки принимаем конструктивно = 16 см
Т.к требуемая площадь полки мала, то ширину полки принимаем конструктивно = 16 см согласно конструктивных требований.
согласно конструктивных требований.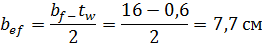

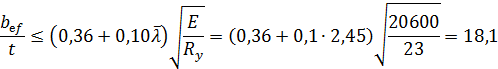
 больше Аr = 40,66 см2
больше Аr = 40,66 см2 


 .
. .
. .
. %, принимаем предварительно подобранное сечение.
%, принимаем предварительно подобранное сечение.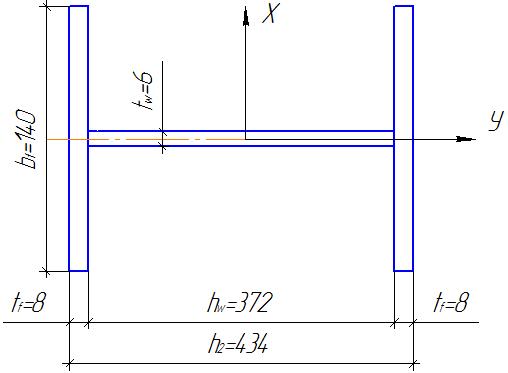



 По табл. 72[2]:
По табл. 72[2]:  0,455.
0,455. ,
, .
. .
. , где по табл. 10 [2]:
, где по табл. 10 [2]: ;
; ,
,  ,
, .
. .
. .
. .
. ,
, ,
,

 , тогда правая часть неравенства будет равна:
, тогда правая часть неравенства будет равна: .
.