
|
|
Профилирование поверхности лопасти.Рабочие колёса с
а полный угол охвата лопасти определяется интегралом
Движение жидкости в колесе с наименьшими гидравлическими потерями обеспечивается условием безотрывного обтекания лопастей потоком. Так как установить аналитическую связь между риг, отвечающую этому условию, практически не представляется возможным, приведенный выше интеграл решается методом численного интегрирования. Для этого среднюю геометрическую линию тока меридианного сечения канала колеса разбиваем на ряд 12—14 равных элементарных отрезков. Обозначая подынтегральную функцию
приращение центрального угла определяем с помощью формулы
где полный угол охвата лопасти находим следующим образом:
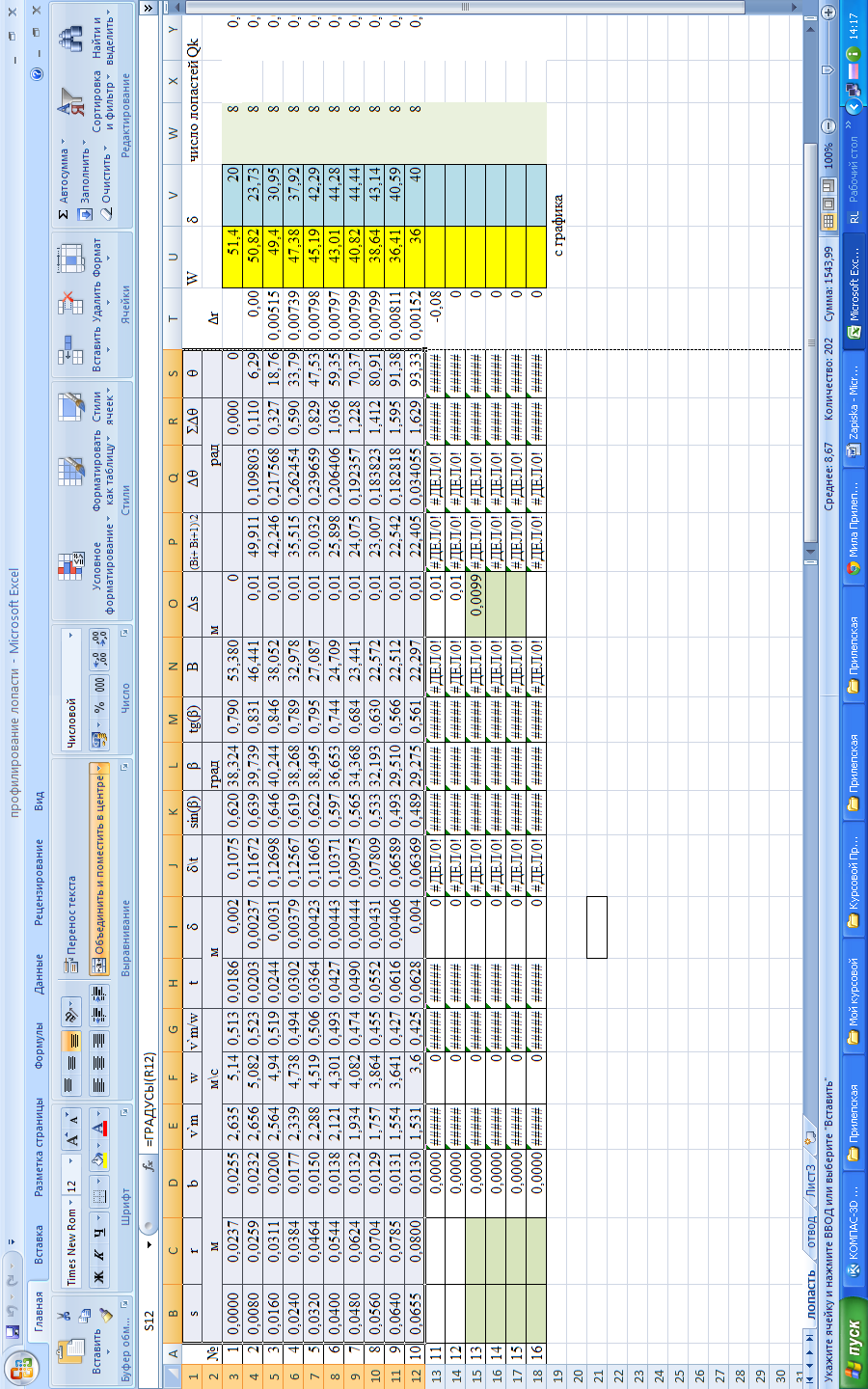
Для определения величины подынтегральной функции задаёмся плавным, максимумов и минимумов, изменением относительной скорости W и толщинылопасти
Отсюда величина угла наклона лопасти
где значения W и δ снимают из графика (рис. 4), а значения шага и меридианной составляющей скорости определяют из соотношений
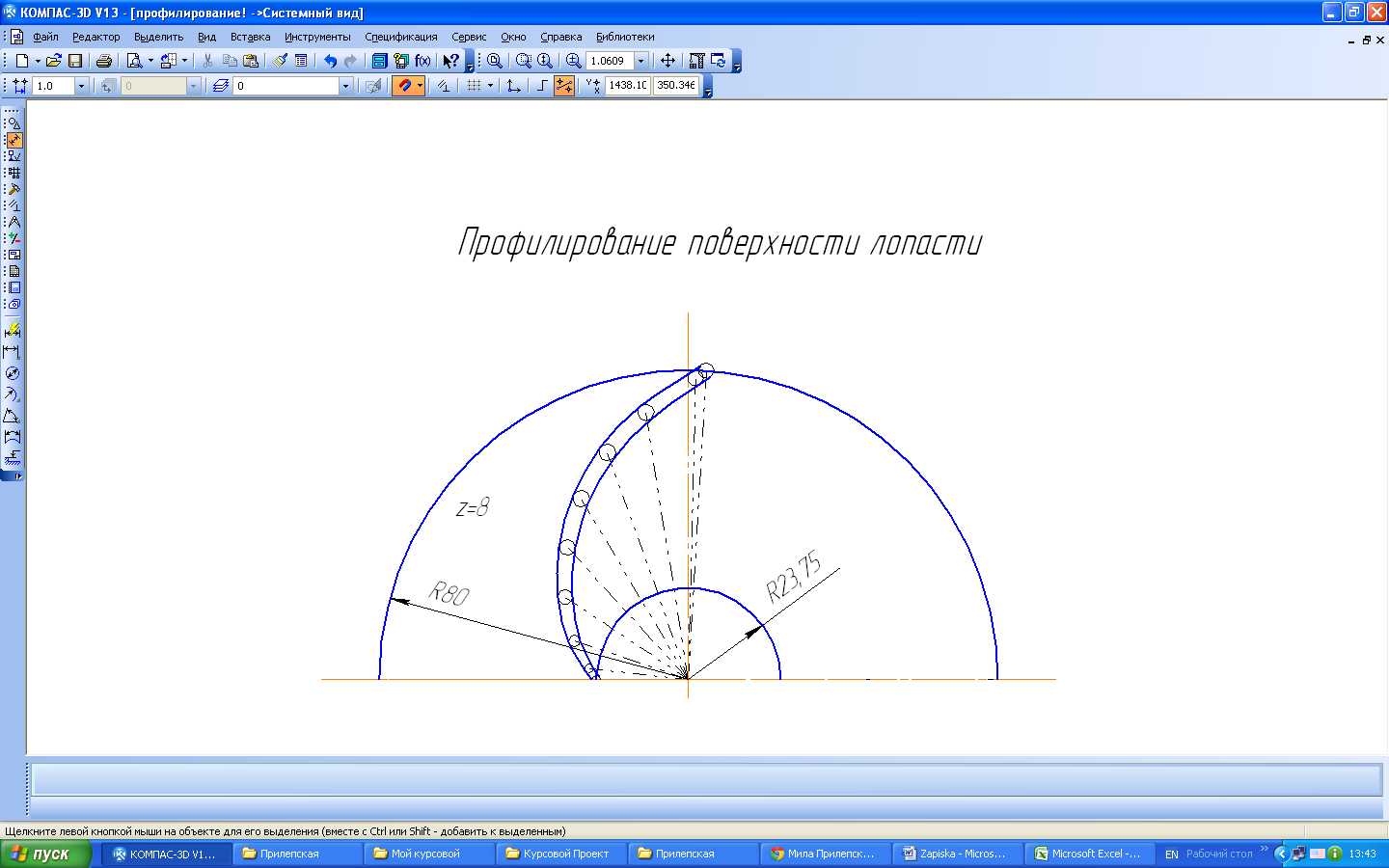
Рис. 4 При определении v'm величину b снимают из чертежа меридианного сечения колеса, составленного предыдущим расчетом. Весь расчет по профилированию поверхности лопасти сводят в табличную форму (табл. 2). Получив, таким образом, значения θ как функцию rнаносят соответствующие точки в плане и строят среднюю линию лопасти, по точкам. Затем, в каждой точке средней линии откладывают соответствующую величину толщины δ лопасти, строят ее контур (рис. 5)
Рис. 5 Таблица 2
Расчет отвода спирального типа Спиральный отвод состоит из спирального канала и диффузора. Спиральный канал служит для сохранения осе симметричности потока за рабочим колесом, необходимой для обеспечения в последнем установившегося относительного движения. Процесс преобразования скорости потока в энергию давления имеет место уже в спиральном канале. Однако скорость потока в сечении устья, спирали все еще остаются значительной величиной, большей, чем значения их в трубопроводе. Дальнейшее уменьшение скорости, а следовательно, преобразование ее в энергию давления осуществляется в диффузоре отвода. Расчет спирального канала производится из условия постоянства в сечениях момента скорости или средней скорости. Расчет будем производить из условия постоянства момента скорости потока. Условие постоянства момента скорости потока во всех сечениях спирального канала, принимаемое в основу расчета, вытекает из условия сохранения осесимметричности потока за рабочим колесом. Условие постоянства момента скорости определяется выражением
где Гс - постоянная спирального отвода. Расход жидкости через сечение спирального канала растет пропорционально центральному углу Величина расхода через любое сечение может быть выражено интегрированием
Зависимость ширины сечения спирального канала Ь от радиуса г выражается графически, поэтому интегрирование проводится в численном виде. Обозначая подынтегральную функцию
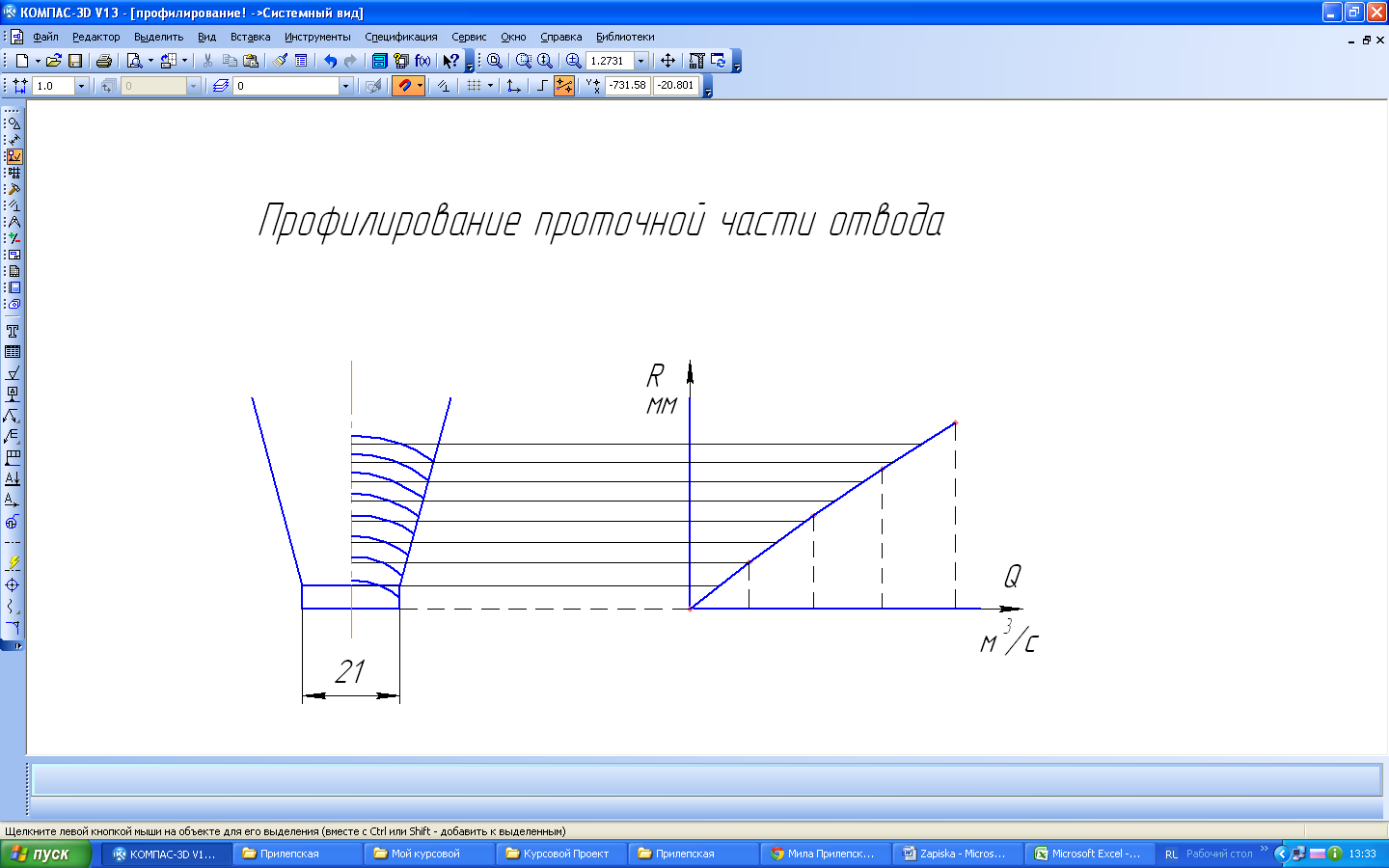
где Размеры спирального отвода рассчитывают в следующей последовательности. Задаются боковыми очертаниями меридианного сечения канала (рис. 6).
Рис.6 Начальную ширину канала принимают
соответственно радиус начальной окружности
Принимаем Приняв некоторое конечное приращение Если боковые очертания остальных сечений спирального канала приняты отличными друг от друга, можно приблизительно принять
т.е. выбрать площадь сечения, расположенного под углом Полученный этим способом контур сечения, ограниченный с внешней стороны цилиндрической поверхностью, не конструктивен как с гидравлической точки зрения, так и по условиям прочности и технологичности. В связи с этим контур заменяют плавными линиями, не изменяя пропускной способности сечения, для чего разность окончательного сечения от расчетного должно быть одинакова, т.е.
где
Весь расчет по отводу спирального типа приведен в таблице 3: Таблица 3

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|

 , имеющие обычные кавитационные качества, выполняют с цилиндрическими лопастями, поскольку у таких колес направление средней линии тока в меридианном сечении совпадает с направлением радиуса. Дифференциальное уравнение средней линии контура лопасти в плане имеет вид
, имеющие обычные кавитационные качества, выполняют с цилиндрическими лопастями, поскольку у таких колес направление средней линии тока в меридианном сечении совпадает с направлением радиуса. Дифференциальное уравнение средней линии контура лопасти в плане имеет вид (4.1)
(4.1) (4.2)
(4.2) (4.3)
(4.3) (4.4)
(4.4) - приращение радиуса, определяемое как разность между радиусами в начале и конце рассматриваемого элементарного отрезка; Bi и Bi+1 - значения подынтегральной функции в начале и конце отрезка
- приращение радиуса, определяемое как разность между радиусами в начале и конце рассматриваемого элементарного отрезка; Bi и Bi+1 - значения подынтегральной функции в начале и конце отрезка (4.5)
(4.5) (рис. 3) в пределах от R1 до R2 . При наличии меридианного сечения канала колеса, полученного предыдущим расчетом, величина относительной скорости
(рис. 3) в пределах от R1 до R2 . При наличии меридианного сечения канала колеса, полученного предыдущим расчетом, величина относительной скорости (4.6)
(4.6) (4.7)
(4.7) (4.8)
(4.8) (4.9)
(4.9)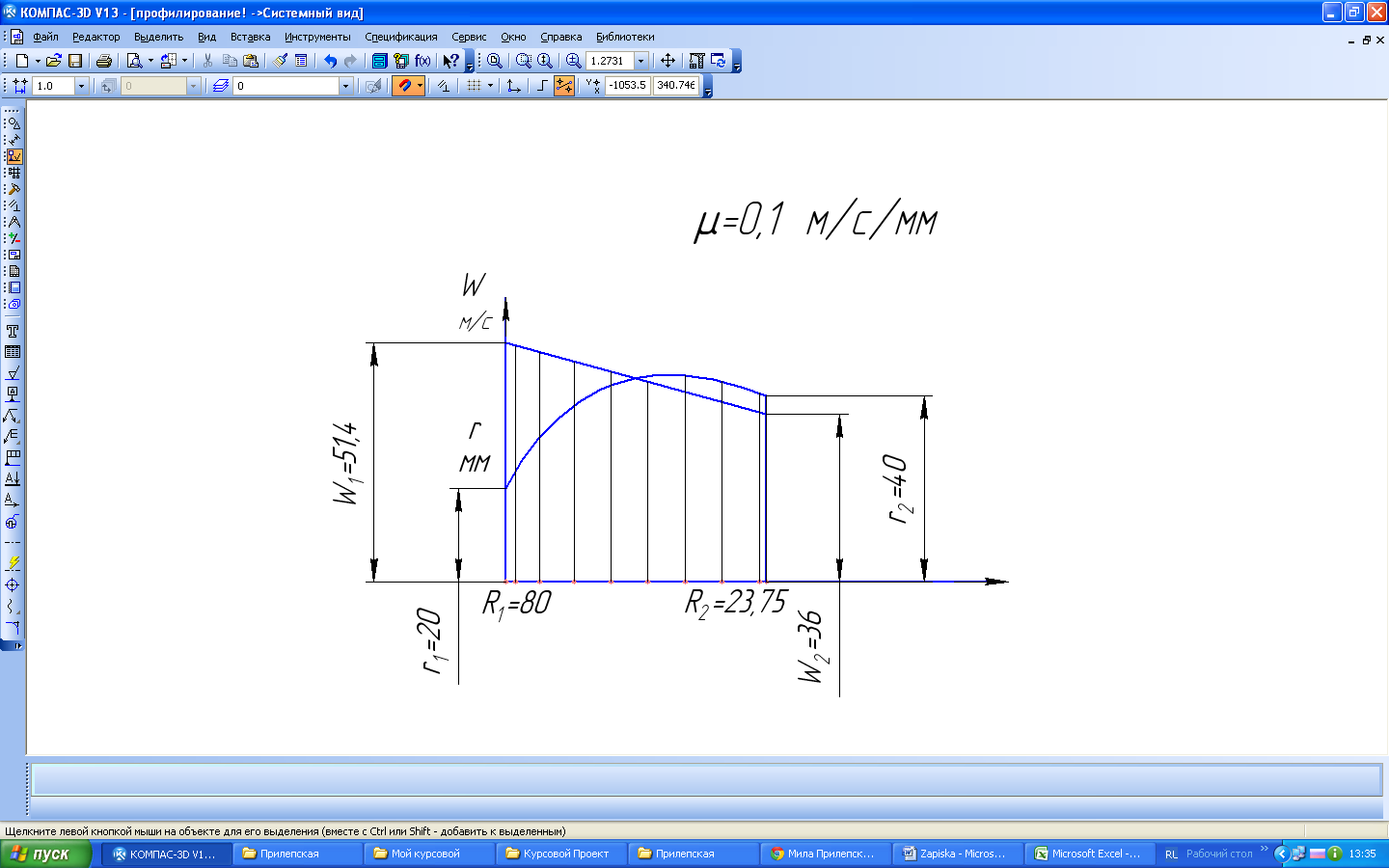
 ,
, и равен
и равен .
.
 , расход через сечение может быть выражен
, расход через сечение может быть выражен ,
, и
и  - значения подынтегральной функции в начале и конце участка, определяемые значениями радиуса r и
- значения подынтегральной функции в начале и конце участка, определяемые значениями радиуса r и  ; i - число участков в границе от r =
; i - число участков в границе от r =  до r =
до r =  .
.
 (мм), Принимаем
(мм), Принимаем  = 21 мм
= 21 мм ,
, мм
мм мм
мм , строим кривую пропускной способности сечений, ограниченных снаружи цилиндрическими поверхностями
, строим кривую пропускной способности сечений, ограниченных снаружи цилиндрическими поверхностями  по приведенному выше указанию для
по приведенному выше указанию для  . Данные расчет приведены в таблице 3. В последней графе таблицы все приращения
. Данные расчет приведены в таблице 3. В последней графе таблицы все приращения  суммируются нарастающим итогом до значения полного расхода
суммируются нарастающим итогом до значения полного расхода  .Обычно строят восемь равноотстоящих друг от друга сечений. Если принять их боковые очертания теми же, то отрезок
.Обычно строят восемь равноотстоящих друг от друга сечений. Если принять их боковые очертания теми же, то отрезок  . Соответствующие расходам
. Соответствующие расходам  ,
,  ,
,  и т.д. Учитывая, что последнее сечение начинается, отступив от поверхности
и т.д. Учитывая, что последнее сечение начинается, отступив от поверхности  на величину толщины зуба спирального отвода, с радиуса
на величину толщины зуба спирального отвода, с радиуса  откладываем полный
откладываем полный  , соответствующей
, соответствующей  . В точке пересечения прямой
. В точке пересечения прямой  с кривой
с кривой  .
.
 , пропорционального углу
, пропорционального углу  от исходного сечения
от исходного сечения  .
. , или, заменяя значения
, или, заменяя значения  и
и  через постоянную спирали получим
через постоянную спирали получим
 и
и  - радиусы положения центров тяжести соответствующих площадок.
- радиусы положения центров тяжести соответствующих площадок.

