
|
|
Расчёт проточной части колеса2.1Определение основных параметров:
1. Подача колеса Q1 = Q/k, (2.1.1) где Q- подача насоса, k- число потоков. Q1 = 2. Напор колеса H1=H/i, (2.1.2) где Н- напор насоса, i- число ступеней насоса.
3. Коэффициент быстроходности ступени
где n- частота вращения колеса в об/мин. 4. Гидравлический к.п.д. ступени
где D1пр- приведенный диаметр колеса (мм), определяемый по формуле:
5. Объёмный к.п.д. ступени (учитывающий потери только в переднем уплотнении колеса)
Внутренний механический к.п.д. ступени (учитывающий только потери дискового трения) в первом приближении может быть определен :
Механический к.п.д. насоса с учетом потерь в сальниках и подшипниках можно принять на (1-3)% меньше, чем ηiм, т.е. ηм=0,911.
6. Общий к.п.д. насоса.
9. Мощность на валу насоса (кВт)
10. Максимальная расчетная мощность на валу насоса
11. Определение диаметра вала и втулки
Выбираем из стандартного ряда размеров d0= 16 мм
Принимаем 3.2 Определение основных размеров колеса: 12. Определение размеров входа в колесо. Расчетная подача насоса:
Скорость потока во входном отверстии колеса:
Диаметр входного отверстия колеса:
Радиус средней точки входной кромки лопасти:
Ширина канала в меридианном сечении на входе колеса:
Меридианная составляющая скорости с учетом стеснения: 1; Переносная скорость средней точки входной кромки лопасти:
Угол, соответствующий безударному поступлению потока на лопасть:
Принимая
13. Определение размеров выхода из колеса. Теоретический напор:
Полагая
И радиус наружной окружности колеса:
Ширина канала на выходе:
Меридианная составляющая абсолютной скорости без учета стеснения:
Меридианная составляющая с учетом стеснения:
Выходной угол лопасти берут в пределах β2=20-30˚.
Коэффициент снижения напора из-за конечного числа лопастей:
Теоретический напор при бесконечном числе лопастей:
Во 2-м приближении
Относительные скорости:
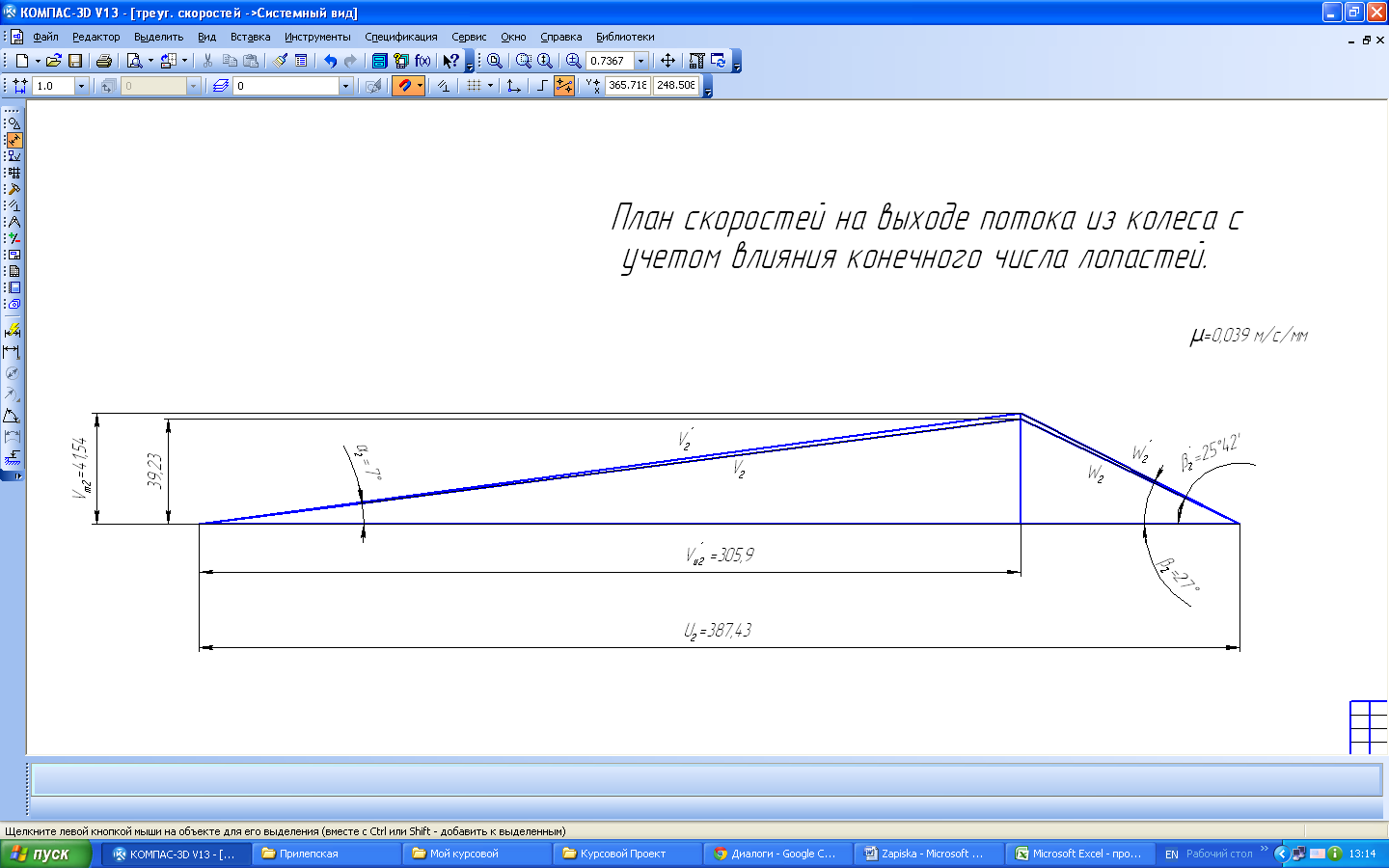
Получив, таким образом, элементы входа и выхода колеса, строим соответствующие планы скоростей при входе в колесо (рис. 2,а) и выходе из колеса с учетом конечного числа лопастей (рис. 2,б).
Рис. 2(а)
Рис. 2(б)
Профилирование канала колеса в меридианном сечении Исходным положением профилирования канала в меридианном сечении для получения высоких энергетических и кавитационных качеств колеса является обеспечение плавности изменения скоростей от входного отверстия колеса и до выхода из него. С этой целью задаются графиком изменения скоростей в функции от радиуса r или длины средней линии канала s. Рабочие колёса с
Рис. 3 Затем наносим линии параллельные оси OZ, отстоящие от последней на расстоянии R1 и R0. Справа строят эпюру скоростей
Результаты приведены в таблице 1. Получив, таким образом, для различных точек ширину канала, проводим окружности с радиусом b/2 касательно к линии АБ. Проводим огибающую к этим окружностям, не доводя до линии R0 . Затем проводим окружность с радиусом R, плавно сопрягающуюся с линией R0. В дальнейшем окружности с радиусами b/2 проводим касательно к дуге окружности радиуса R. Таким же образом проводим справа (по контуру, соответствующему ведущему диску) огибающую до сопряжения с линией OZ. В случае необходимости контуры канала корректируют по конструктивно-технологическим соображениям и определяют окончательное положение средней линии тока. Таблица 1.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|


 , (2.1.3)
, (2.1.3)
 (2.1.4)
(2.1.4) (2.1.5)
(2.1.5)

 (2.1.6)
(2.1.6)
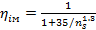
 (2.1.7)
(2.1.7) (2.1.8)
(2.1.8) =0,858*0,972*0,911=0,759
=0,858*0,972*0,911=0,759 (2.1.9)
(2.1.9)
 ,
, =1,3*1,25=1,625кВт (2.1.10)
=1,3*1,25=1,625кВт (2.1.10) (2.1.11)
(2.1.11)
 =22мм (2.1.12)
=22мм (2.1.12) (2.2.1)
(2.2.1) (2.2.2)
(2.2.2) (2.2.3)
(2.2.3) ;
;  (2.2.4)
(2.2.4) ; (2.2.5)
; (2.2.5) ; (2.2.6)
; (2.2.6) ; (2.2.7)
; (2.2.7) ;
;  (2.2.8)
(2.2.8) , имеем угол наклона лопасти на входе:
, имеем угол наклона лопасти на входе: (2.2.9)
(2.2.9) (2.2.10)
(2.2.10) имеем в 1-м приближении значение переносной скорости на выходе:
имеем в 1-м приближении значение переносной скорости на выходе: ; (2.2.11)
; (2.2.11) (2.2.12)
(2.2.12) (2.2.13)
(2.2.13) (2.2.14)
(2.2.14) (2.2.15)
(2.2.15)
 ; zK=8.
; zK=8.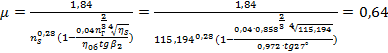 (2.2.16)
(2.2.16) (2.2.17)
(2.2.17) (2.2.18)
(2.2.18) ; Δ=0,4%. (2.2.19)
; Δ=0,4%. (2.2.19) Δ=0,93%. (2.2.20)
Δ=0,93%. (2.2.20) Δ=0,94%. (2.2.21)
Δ=0,94%. (2.2.21) (2.2.22)
(2.2.22) (2.2.23)
(2.2.23)

 имеют цилиндрические лопасти, расположенные в радиальной части канала. Профилирование канала колеса в меридианном сечении производят в следующей последовательности. На ось вращения OZ (рис. 3) наносим перпендикулярно к ней линию. На расстоянии R2 откладываем отрезок, равный b2.
имеют цилиндрические лопасти, расположенные в радиальной части канала. Профилирование канала колеса в меридианном сечении производят в следующей последовательности. На ось вращения OZ (рис. 3) наносим перпендикулярно к ней линию. На расстоянии R2 откладываем отрезок, равный b2.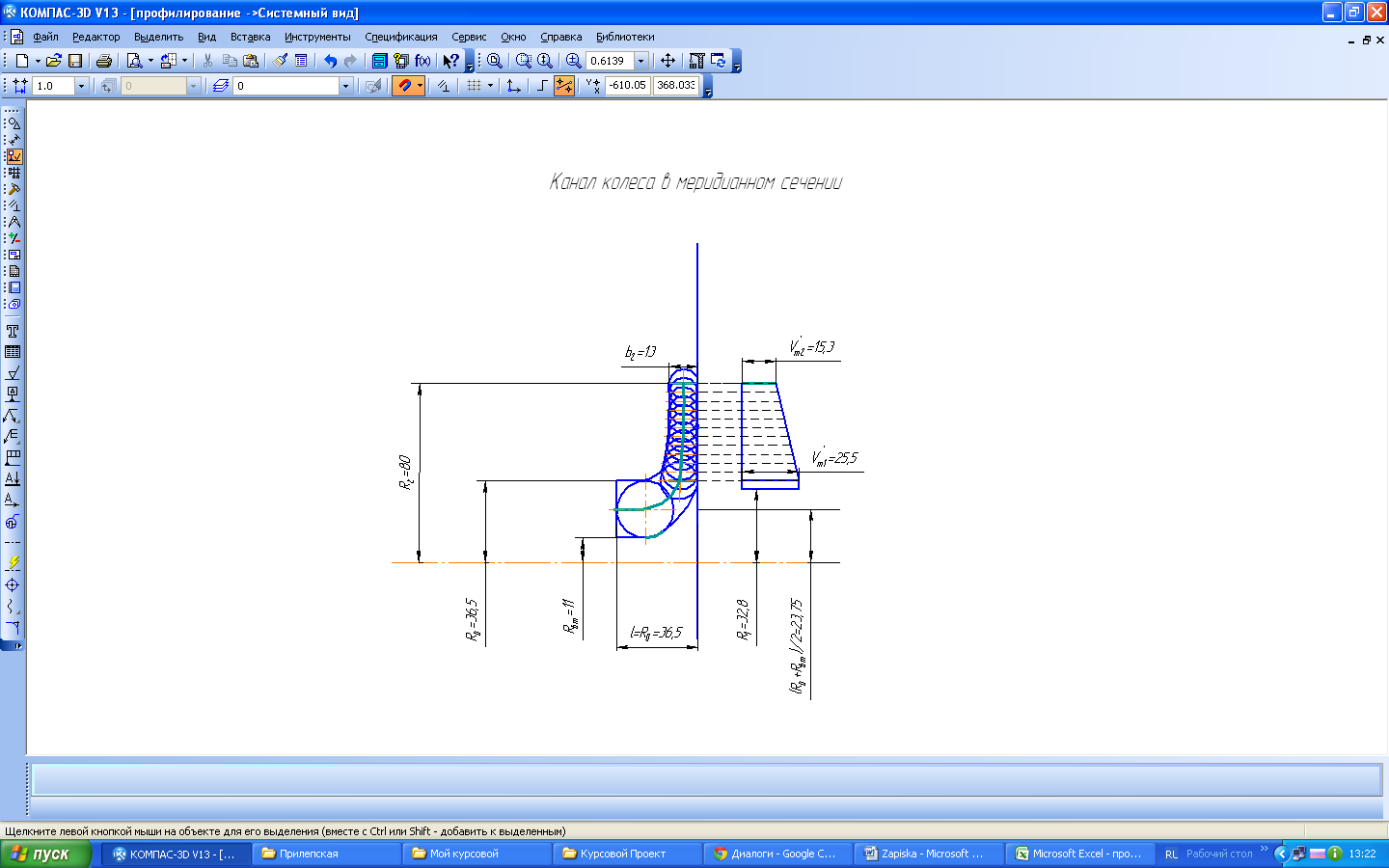
 , изменяющейся по радиусу прямолинейно от
, изменяющейся по радиусу прямолинейно от  до
до  . При этом в соответствии с указанным выше принимаем
. При этом в соответствии с указанным выше принимаем  =
=  . Имея для любой точки произвольного радиуса r величину
. Имея для любой точки произвольного радиуса r величину  (3.1)
(3.1)