
|
|
Временные параметры сетевых моделей
Пример. Определить временные параметры событий и критический путь для сетевого графика.
Для i=0 (нулевого события), очевидно, что tp(0)=0. Для i=1 tp(1)= tp(0)+ t(0,1)=0+8=8 (суток), так как для события 1 существует только один предшествующий путь (0®1). Для i=2 tp(2)= tp(1)+ t(1,2)=8+9=17 (суток), так как для события 2 существует только один предшествующий путь (0®1®2). Для i=3 tp(3)=max{ tp(0)+ t(0,3); tp(1) + t(1,3)}= max{ 0+13;8+4}=13(суток) так как для события 3 существует два предшествующих пути и два предшествующих события. tp(4)=max{ tp(1)+ t(1,4); tp(3) + t(3,4)}= max{ 8+6;13+10}=23(суток) и т.д.
Длина критического пути равна раннему сроку свершения завершающего события 11 tkp =61 (сутки). 3.4. График привязки Для проведения анализа временных параметров сетевой моделииспользуют график привязки, который отображает взаимосвязь выполняемых работ во времени. По вертикальной оси графика привязки откладываются коды работ, по горизонтальной оси – отрезки, соответствующие длительностям работ (раннее начало и раннее окончание работ). График привязки можно построить на основе данных о продолжительности работ. При этом необходимо помнить, что работа При поиске критических путей следует помнить, что признаком критической работы являются нулевые значения резервов времени. Это означает, что каждая последующая критическая работа будет начинаться строго в момент окончания предыдущей критической работы. Вследствие этого сдвиг любой из работ критического пути обязательно приведет к увеличению первоначальной длительности проекта. Кроме того, следует учесть, что критический путь является полным, т.е. соединяет исходное и завершающее события сети. Поэтому на графике привязки первая из работ критического пути всегда начинается в исходном событии сети с нулевого (начального) момента времени, а последняя из работ критического пути всегда завершается позже всех остальных работ сети в завершающем событии. Способ определения критического пути на графике привязки (все найденные работы выписываются последовательно справа налево): 1) найти на графике привязки и выписать работу (i,j), которая заканчивается позже всех остальных. Это будет последняя работа критического пути (ее конечное событие иметь номер завершающего события сети); 2) из всех работ сети (k,i), конечное событие которых i совпадает с начальным событием i работы (i,j), найденной в п.1), выбрать и выписать ту, которая на графике вплотную примыкает к работе (i,j); 3) из всех работ сети (l,k), конечное событие которых k совпадает с начальным событием k работы (k,i), найденной в п.2), выбрать и выписать ту, которая на графике вплотную примыкает к работе (k,i); 4) продолжать п.3) до тех пор, пока не будет найдена исходная работа сети, т.е. начинающаяся в нулевой момент времени (ее начальное событие будет иметь номер исходного события сети, например, 1). Пример По данным о кодах и длительностях работ в днях постройте график привязки сетевой модели, определите критические пути и их длительность. Определите свободные и полные резервы каждой работы, отметьте на графике привязки свободные резервы работ.
Решение 1) Построим график привязки (рис.8.4).
2) Начнем поиск критических путей (справа налево) с работ, завершающих проект. На графике привязки (см. рис.8.4) две работы (6,7) и (3,7), которые заканчиваются позже остальных в завершающем событии №7. Записываем работы, определенные как критические справа налево
3) Найдем критическую работу из
4) Найдем критическую работу из
5) Найдем критическую работу из
6) Аналогичный поиск работ критического пути В другой форме записи 7) Для наглядности выделим на графике привязки критические работы жирной линией. II. Поиск резервов работ 1) Для всех найденных критических работ впишем в табл.3 нулевые значения свободного и полного резервов. Рассмотрим некритические работы, начиная с конца табл.8.3.
2) Работа (5,7), согласно графику привязки (см. рис.8.4) заканчивается в 13-й день, а завершающее событие 7 сети, в которое она входит, наступает лишь в 14-й день. Т.е. если работа (5,7) задержится на 1 день, то это не повлияет на срок выполнения проекта ( 3) Работа (4,6) заканчивается в 8-й день, в то время как последующая работа (6,7) начинается в 10-й день. То есть, работа (4,6) может задержаться на 2 дня и это никак не повлияет на время начала последующей работы (6,7), т.е. За работой (4,6) следует только критическая работа (6,7) с нулевым полным резервом. Поэтому 4) Работа (4,5) заканчивается в 12-й день, в этот же день начинается следующая работа (5,7), т.е. любая задержка выполнения работы (4,5) приведет к задержке начала работы (5,7). Это означает, что работа (4,5) не имеет свободного резерва
5) Работа (1,5) заканчивается в 10-й день, в то время как последующая работа (5,7) начинается в 12-й день. Т.е. работа (1,5) может задержаться на 2 дня и это никак не повлияет на время начала последующей работы (5,7), т.е.
6) Работа (1,4) заканчивается во 2-й день, и в этот же день начинаются следущие работы (4,5) и (4,6). Т.е. работа (1,4) не имеет свободного резерва времени
7) Работа (1,3) заканчивается в 3-й день, а следующие за ней работы (3,6) и (3,7) начинаются в 5-й день, т.е.
8) Ненулевые свободные резервы работ обозначены на графике привязки фигурными скобками (см. рис.8.4).

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|




 может выполняться только после того как будут выполнены все предшествующие ей работы
может выполняться только после того как будут выполнены все предшествующие ей работы  .
.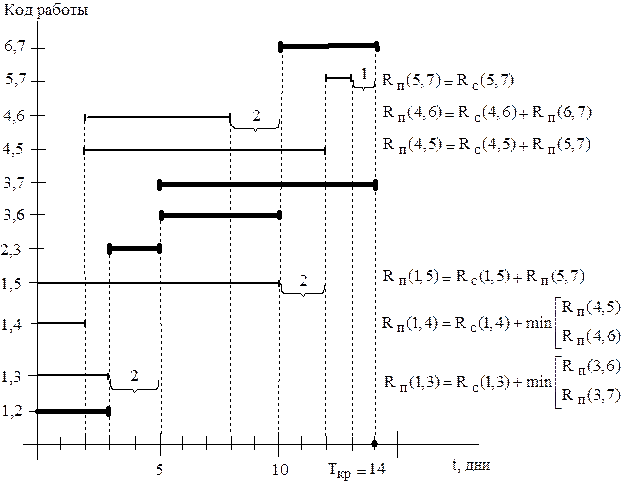
 ;
;
 .
. , предшествующую (6,7). Код этой работы должен оканчиваться на 6. Таких работ две – (4,6) и (3,6). Но только одна из них, работа (3,6) по времени своего окончания вплотную "примыкает" на графике к началу работы (6,7). Допишем слева найденную критическую работу (3,6) к выражению (8.1)
, предшествующую (6,7). Код этой работы должен оканчиваться на 6. Таких работ две – (4,6) и (3,6). Но только одна из них, работа (3,6) по времени своего окончания вплотную "примыкает" на графике к началу работы (6,7). Допишем слева найденную критическую работу (3,6) к выражению (8.1)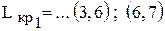 .
.
 .
.
 .
. приводит к результату
приводит к результату  .
. и
и  .
.



 дней). Поскольку (5,7) завершающая работа сети, то ее полный и свободный резервы равны
дней). Поскольку (5,7) завершающая работа сети, то ее полный и свободный резервы равны  .
. .
. .
.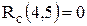 . Но если сдвинуть во времени работу (4,5) на 1 день, то работа (5,7) также сдвинется на 1 день и это не нарушит срок выполнения проекта, т.к. у работы (5,7) есть временной резерв. Таким образом согласно правилу №8.1
. Но если сдвинуть во времени работу (4,5) на 1 день, то работа (5,7) также сдвинется на 1 день и это не нарушит срок выполнения проекта, т.к. у работы (5,7) есть временной резерв. Таким образом согласно правилу №8.1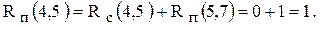
 . Кроме того, поскольку последующая работа (5,7) имеет резерв в 1 день, то, в общем, работу (1,5) можно сдвинуть на 3 дня и это не нарушит сроков проекта (см. рис.8.4), т.е.
. Кроме того, поскольку последующая работа (5,7) имеет резерв в 1 день, то, в общем, работу (1,5) можно сдвинуть на 3 дня и это не нарушит сроков проекта (см. рис.8.4), т.е.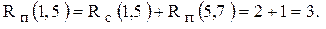
 . Поскольку после работы (1,4) следуют две работы с различными полными резервами, то согласно правилу №8.1
. Поскольку после работы (1,4) следуют две работы с различными полными резервами, то согласно правилу №8.1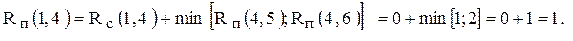
 . Поскольку обе последующие работы критические, то полный и свободный резерв работы (1,3) совпадают
. Поскольку обе последующие работы критические, то полный и свободный резерв работы (1,3) совпадают .
.