
|
|
Уравнение прямой, заданной точкой12 Вектором нормали Рассмотрим в прямоугольной декартовой системе координат Оху произвольную прямую d. Пусть на этой прямой задана точка
М0 d
О Рис. 2.19
Уравнение прямой с угловым коэффициентом В прямоугольной системе координат уравнение прямой d:
y d
b
О Рис. 2.20 Примеры решения задач 1. Составить уравнение прямой, проходящей через точку А(–2; 3) и перпендикулярной вектору Решение Составим уравнение прямой, используя формулу (7)
2. Даны координаты вершин А(1; –2), В(3; 2) и центра Е(1; 1) параллелограмма АВСD. Написать уравнения сторон параллелограмма. Решение
Рис. 2.21
В параллелограмме ABCD (рис. 2.21)
Теперь у каждой стороны известны два определяющих элемента, что позволит составить их уравнения:
3. Прямая, проходящая через точку А (–2; 3), образует с осью Ох угол 135о. Составить уравнение этой прямой. Решение Уравнение прямой будем искать в виде Расстояние от точки до прямой. Угол между прямыми В прямоугольной системе координат расстояние от точки
Угол j между прямыми
Если прямая задана уравнением с угловым коэффициентом
Перпендикулярность двух прямых определяется условием:
Очевидно, что векторы
Примеры решения задач 1. Дана прямая d: Решение Искомое расстояние вычисляется по формуле (1) 2. Стороны треугольника АВС заданы уравнениями Решение
3. Вычислить угол j между прямыми Решение По формуле (2) находим
т. е. j = 900 и прямые взаимно перпендикулярны. Задачи для практических занятий 1. Пусть АВСD — параллелограмм, О — точка пересечения диагоналей, M, N, P, Q — соответственно середины сторон АВ, ВС, СD, DА. Построить на чертеже следующие векторы: а) д) 2. Точки М и N — середины сторон треугольника АВС. Выразить векторы 3. В треугольнике АВС векторы 4. Пусть АВСD — параллелограмм, а О — точка пересечения его диагоналей. Полагая 5. Определить расстояния между точками А1(2; –1) и А2(1; 2); 6. Даны точки А(0; 0), В(3; –4), С(–3; 4), D(–2; 2) и Е(10; –3). Найти длины отрезков АВ, ВС, АС, CD, AD, DE. 7. Даны вершины треугольника А(3; 2), В(–1; –1) и С(11; –6). Вычислить длины его сторон. 8. Даны две смежные вершины квадрата А(3; –7) и В(–1; 4). Вычислить его площадь. 9. Даны две противоположные вершины квадрата H(3; 5) и М(1; –3). Вычислить его площадь. 10.Вычислить площадь правильного треугольника, две вершины которого А(–3; 2) и В(1; 6). 11.Определить длину медианы АМ треугольника АВС, заданного координатами своих вершин: А(5; –4), В(–1; 2), С(5; 1). 12.На оси абсцисс найти такую точку М, расстояние от которой до точки К(2; –3) равнялось бы 5. 13.На оси ординат найти такую точку М, расстояние от которой до точки К(–8; 13) равнялось бы 17. 14.Даны концы отрезка АВ: А(3; –5) и В(–1; 1). Найти координаты его середины. 15.Середина отрезка находится в точке М(1; 4), один из его концов в точке Р(–2; 2). Определить координаты другого конца К этого отрезка. 16.Даны вершины треугольника А(1; –3), В(3; –5) и С(–5; 7). Определить середины его сторон. 17.Даны вершины треугольника А(3; –7), В(5; 2) и С(–1; 0). Определить середины его сторон. 18.Определить координаты точек, делящих отрезок АВ: А(2; 3), 19.Определить координаты концов А и В отрезка, который точками Р(2; 2) и М(1; 5) разделен на три равные части. 20.Вычислить площадь треугольника АВС, заданного координатами вершин, в каждом из следующих случаев: а) А(2; 1), В(3; 4), С(1; 6); б) А(–2; 4), В(0; –3), С(1; 7); в) А(5; 4), В(11; 0), С(0; 3). 21. Вычислить площадь треугольника АВС, заданного координатами вершин, в каждом из следующих случаев: а) А(2; –3), В(3; 2), С(–2; 5); б) А(–3; 2), В(5; –2), С(1; 3); в) А(3; –4), В(–2; 3), С(4; 5). 22.Вершины треугольника А(3; 6), В(–1; 3) и С(2; –1). Вычислить длину его высоты, проведенной из вершины С. 23.Вычислить площадь параллелограмма, если известны координаты его трех вершин А(–2; 3), В(4; –5) и С(–3; 1). 24.Площадь треугольника равна 3, две его вершины А(3; 1) и 25.Площадь треугольника равна 4, две его вершины А(2; 1) и 26.Вычислить скалярное произведение векторов 27.В равностороннем треугольнике АВС со стороной а проведена высота ВН. Вычислить скалярное произведение векторов: а) 28.Вычислить скалярное произведение векторов а) 29.Доказать, что ненулевые векторы 30.Доказать, что векторы 31.При каком значении х векторы 32.Найти косинусы углов треугольника с вершинами А(2; 8), 33.Найти углы треугольника с вершинами А(–1; 34.Известно, что вектор 35. Дана прямая 2х – у + 5 = 0. Выяснить, какие из следующих точек принадлежат данной прямой: (5; 15), (1; 1),(–2; 1), (3; 0), (7; –5), 36. Определить координаты точек, которые принадлежат прямой 37. Определить координаты точек, которые принадлежат прямой 7х + 2у – 8 = 0 и имеют абсциссы 2; –4; 3; –1; 1; 0,5. 38. Построить прямые: а) 39. Написать уравнение прямой: а) проходящей через точки А(–1; 1) и В(2; 5); б) проходящей через начало координат и точку А(2; 5); в) проходящей через точку А(2; –6) и параллельной вектору г) отсекающей на осях координат отрезки а = 3, b = –2; д) проходящей через точку А(3; 5) и параллельной оси Ох; е) проходящей через точку В(–1; 2) и параллельной оси Оу; ж) проходящей через точку А(1; –5) и параллельной прямой 40. Записать общие уравнения прямой и укажите координаты вектора нормали к данной прямой: а) 41. Найти точки пересечения следующих пар прямых: а) 42. Даны уравнения сторон треугольника 43. Треугольник АВС задан координатами своих вершин А(–1; 3), В(0; 4), С(–2, –2). Написать уравнение медианы этого треугольника, проведенной из вершины А. 44.Установить, какие из следующих троек точек лежат на одной прямой: а) (2; 1), (–1; 4), (–7; 10); в) (1; 0), (0; 1), (–2; 3); б) (0; 5), (7; 1), (–2; 3); г) (2; 1), (10; 3), (5; 2). 45. Найти координаты направляющих векторов следующих прямых: а) 3х + 7у = 0; б) х + 5 = 0; в) 2х – 3у – 1 = 0; г) –х + 2у – 8 = 0; д) 2у + 5 = 0. 46. Даны три вершины треугольника: А(1; –2), В(0; 3), С(1; 1). Написать уравнения прямых, проходящих через каждую из них параллельно противоположной стороне. 47. Записать уравнение прямой, проходящей через точку М (0; в) и имеющей угловой коэффициент k: а) М(0; –2), k = 1; б) М(0; 1), k = –3; в) М(0, 0), k=-2; г) М(0, 0), k=0. 48. Написать уравнения прямых, отсекающих на положительной оси Оу отрезок, равный 4, и образующих с осью Ох углы: а) 30о; б) 45о; 49. Написать уравнение прямой: а) проходящей через точку А(2; 5) и имеющей угловой коэффициент k = 3; б) проходящей через точку (0; 0) и имеющей угловой коэффициент в) являющейся биссектрисой координатного угла хОу; г) проходящей через начало координат и образующей с осью Ох угол 30о; д) проходящей через начало координат и образующей с осью Ох угол 120о; е) отсекающей от оси Оу отрезок b = 2 и имеющей угловой коэффициент k = –3; ж) отсекающей от оси Оу отрезок b = –3 и имеющей угловой коэффициент k = 1. 50. Найти угловые коэффициенты и отрезки, осекаемые на оси Оу каждой из следующих прямых: а) 2х + у + 5 = 0; б) х – 3у + 6 = 0; в) х + у = 0; г) 2у + 5 = 0; д) 3х + 1 = 0. 51. Найти углы наклона к оси Ох прямых: а) х + у – 7 = 0; б) х – у + 2 = 0; в) х+ 52. Написать уравнение прямой: а) проходящей через точку А(–1; 3) и перпендикулярной к вектору б) проходящей через точку В(5; 10) и перпендикулярной к прямой в) проходящей через начало координат и перпендикулярной к прямой 2х – 3у + 1 = 0. 53. Дана прямая 2х – 5у + 3 = 0. Определить координаты направляющего вектора 54. Даны точки А(2; –3), В(3; –5). Через середину отрезка АВ провести прямую, перпендикулярную к АВ. 55. Даны последовательно вершины выпуклого четырехугольника А(–6; –2) В(6; 7), С(9; 3) и D(1, –3). Определить точку пересечения его диагоналей. 56. Какая из прямых 57. Вершины треугольника имеют координаты А(2; 6), В(–6; 0) и 58. Составить уравнение прямой, проходящей через точку А(–2; 8) и середину отрезка МN, где М(4; 5) и N (–2; –1). 59. Составить уравнение прямой, проходящей через точку А(4; –7) и параллельной прямой PQ, где P(–4; 3) и Q(2; –5). 60. Даны две точки А(–1; 6) и В(9; –8). Через середину отрезка АВ провести прямую, параллельную прямой 61. Найти расстояние d от точки А(6; –8) до прямой, проходящей через точки М1(–5; 0) и М2(3; 6). 62. Найти расстояния от точек А(1; 2), В(–1; 3) и С(1; 6) до прямой 63. В каждом из следующих случаев найти угол, образованный двумя прямыми, заданными в определенном порядке своими уравнениями: а) 3х + у – 6 = 0, 2х – у + 5 = 0; б) в) х – 2у + 1 = 0, 6х + 3у – 2 = 0: г) 64. Дан треугольник с вершинами в точках А(3; 6), В(–1; 3) и 65. Даны уравнения сторон треугольника АВС: (АВ) 66. Найти угол между прямой

12 Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 , а также задан ненулевой вектор
, а также задан ненулевой вектор  (рис. 2.19). Составим вектор
(рис. 2.19). Составим вектор  .
.


 х
х — (7) уравнение прямой, заданной нормальным вектором
— (7) уравнение прямой, заданной нормальным вектором  и точкой
и точкой 
 — (8) уравнение прямой с угловым коэффициентом, b — отрезок отсекаемый прямой от оси Оу (рис. 2.20),
— (8) уравнение прямой с угловым коэффициентом, b — отрезок отсекаемый прямой от оси Оу (рис. 2.20),  , где
, где  — угол между прямой и положительным направлением оси Ох.
— угол между прямой и положительным направлением оси Ох.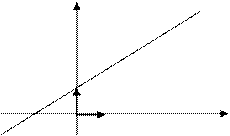

 .
.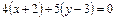 ,
,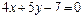 — уравнение искомой прямой.
— уравнение искомой прямой.
 , поэтому Е — середина АС. Используя формулы координат середины отрезка, получим:
, поэтому Е — середина АС. Используя формулы координат середины отрезка, получим: С (1; 4).
С (1; 4).
 || СD.
|| СD. .
. .
. ||
|| 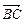 (-2,2).
(-2,2). .
. . Искомая прямая
. Искомая прямая  проходит через точку А(–2; 3), поэтому координаты этой точки
проходит через точку А(–2; 3), поэтому координаты этой точки  и
и  удовлетворяют уравнению данной прямой, т. е.
удовлетворяют уравнению данной прямой, т. е. 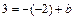 , откуда b=1. Следовательно, уравнение прямой имеет вид
, откуда b=1. Следовательно, уравнение прямой имеет вид  или
или  .
. до прямой
до прямой  вычисляется по формуле
вычисляется по формуле . (1)
. (1) и
и  определяется как острый угол между их направляющими векторами
определяется как острый угол между их направляющими векторами  .
. . (2)
. (2) . Тогда приведенные формулы приобретают вид:
. Тогда приведенные формулы приобретают вид: (3)
(3) или
или  .
.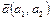 и
и  взаимно перпендикулярны. Этот факт можно использовать для составления уравнения перпендикуляра к данной прямой или направлению.
взаимно перпендикулярны. Этот факт можно использовать для составления уравнения перпендикуляра к данной прямой или направлению. . Найти расстояние от этой прямой до точки А(–1; 3).
. Найти расстояние от этой прямой до точки А(–1; 3).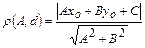 =
= 
 ,
,  . Найти длину высоты BH данного треугольника.
. Найти длину высоты BH данного треугольника.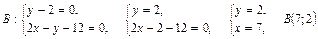 .
. .
. и
и  .
. ,
, б)
б)  в)
в) 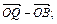 г)
г) 
 е)
е)  ж)
ж) 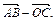
 через векторы
через векторы  .
. направлены по медианам. Выразить их через векторы
направлены по медианам. Выразить их через векторы 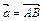 и
и 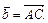
 и
и 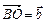 , выразить через
, выразить через  и
и  векторы
векторы  и
и 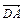 .
.
 и
и  , если
, если 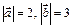 , а угол между ними равен: а) 45о; б) 90о; в) 135о.
, а угол между ними равен: а) 45о; б) 90о; в) 135о. ; б)
; б)  ; в)
; в) 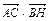 ; г)
; г)  .
. ; б)
; б) 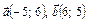 ; в)
; в) 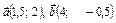 .
.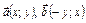 перпендикулярны.
перпендикулярны.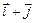 и
и  перпендикулярны, если
перпендикулярны, если  — координатные векторы.
— координатные векторы. ; б)
; б)  ; в)
; в)  ?
?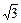 ), В(1; –
), В(1; –  ;
; 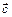 составляет с каждым из векторов
составляет с каждым из векторов  и
и  углы по 60о. Вычислить
углы по 60о. Вычислить  , если
, если  .
.

 б)
б) 

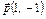 ;
; б)
б) 

 и
и  б)
б) 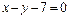 и
и 
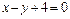 ,
,  ,
,  , найти координаты его вершин.
, найти координаты его вершин.
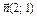 ;
;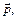 нормального вектора
нормального вектора  угловой коэффициент k и отрезки а и b, отсекаемые на осях координат данной прямой.
угловой коэффициент k и отрезки а и b, отсекаемые на осях координат данной прямой. или
или  отсекает на оси ординат больший отрезок?
отсекает на оси ординат больший отрезок? .
.

 ,
,  .
. , (ВС)
, (ВС)  , (АС)
, (АС)  . Найти длину высоты опущенной из вершины В на сторону АС.
. Найти длину высоты опущенной из вершины В на сторону АС. и прямой, проходящей через точки А(1; –1) и В(5; 7).
и прямой, проходящей через точки А(1; –1) и В(5; 7).