Уравнение прямой, заданной двумя точками
Глава II. «Элементы аналитической геометрии»
§ 1. Векторы. Сложение и вычитание векторов.
Модуль вектора. Умножение вектора на число
Определение. Отрезок называется направленным (рис. 2.1), если указан порядок, в котором заданы концы отрезка.
 Обозначение: Обозначение: 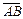 . А В . А В
Рис. 2.1
Определение. Длиной направленного отрезка 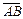 называется длина отрезка АВ. называется длина отрезка АВ.
Обозначение: 
Определение. Ненулевые отрезки 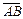 и и  называются одинаково (противоположно) направленными, если одинаково (противоположно) направлены лучи АВ и СD. называются одинаково (противоположно) направленными, если одинаково (противоположно) направлены лучи АВ и СD. 
Обозначение: 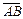  ( ( 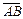 ¯ ¯  ). ).
Определение. Вектором называется множество всех одинаково направленных отрезков, имеющих равные длины. Каждый из этих направленных отрезков называется представителем вектора.
Определение. Два вектора  и и  называются одинаково (противоположно) направленными, если одинаково (противоположно) направлены какие-либо два представителя этих векторов. называются одинаково (противоположно) направленными, если одинаково (противоположно) направлены какие-либо два представителя этих векторов.
Определение. Пусть заданы два вектора  и и  . .  Направленный отрезок Направленный отрезок  определяет вектор определяет вектор 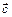 , который называется суммой векторов , который называется суммой векторов  и и  . .
 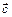 = =  + + 
 B B 
 
А 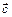 С С
Рис. 2.2
Правило треугольника:  (рис. 2.2). (рис. 2.2).
Откладывая векторы последовательно, можно найти сумму любого количества векторов, используя правило многоугольника (рис. 2.3).
D E

C
A B
Рис. 2.3
 (рис. 2.3). (рис. 2.3).
Для любых векторов  : :
1)  + +  = =  + +  — коммутативность сложения; — коммутативность сложения;
2)  — ассоциативность сложения. — ассоциативность сложения.
Определение. Разностью векторов  и и  называется такой вектор называется такой вектор  , что , что  , ,  . .
Из треугольника ABC (рис. 2.4):  . .
B


А  С С
Рис. 2.4
Правило параллелограмма:  (рис. 2.5). (рис. 2.5).
В С

А D
Рис. 2.5
Определение. Произведением вектора  на действительное число a называется вектор на действительное число a называется вектор  , удовлетворяющий условиям: , удовлетворяющий условиям:
1.  ; 2. ; 2.  , если a ³ 0, , если a ³ 0,  , если a < 0. , если a < 0.
Теорема. Для любых векторов  и для любых действительных чисел a и b выполняются равенства: и для любых действительных чисел a и b выполняются равенства:
1.  ; 2. ; 2.  ; ;
3.  ; 4. ; 4.  . .
Определение. Векторы  и и  называются коллинеарными, если существует прямая, которой они параллельны. называются коллинеарными, если существует прямая, которой они параллельны.
Теорема. Пусть  . Векторы . Векторы  и и  коллинеарны тогда и только тогда, когда их соответствующие координаты пропорциональны, т. е. коллинеарны тогда и только тогда, когда их соответствующие координаты пропорциональны, т. е.  . .
Теорема. Пусть 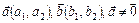 . Векторы . Векторы  и и  коллинеарны тогда и только тогда, когда определитель, составленный из их координат, равен нулю, т. е. коллинеарны тогда и только тогда, когда определитель, составленный из их координат, равен нулю, т. е.  . .
Определение. Коэффициенты  разложения вектора разложения вектора  по координатным векторам по координатным векторам  в прямоугольной системе координат называются координатами вектора в прямоугольной системе координат называются координатами вектора  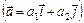 . .
Обозначение:  . .
Координаты вектора  можно вычислить, зная координаты начала и конца этого вектора, т. е. если можно вычислить, зная координаты начала и конца этого вектора, т. е. если  и и  , то , то  . .
Определение. Скалярным произведением двух векторов  и и  называется произведение длин этих векторов на косинус угла между ними. называется произведение длин этих векторов на косинус угла между ними.
Обозначение: 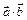 или или   , ,   = =  . .
Теорема. Длина вектора  ( (  ) в прямоугольной системе координат (О, ) в прямоугольной системе координат (О,  ) вычисляется по формуле ) вычисляется по формуле 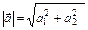 . .
Скалярное произведение 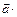  = =  называется скалярным квадратом вектора называется скалярным квадратом вектора  , причем , причем  = =  . Таким образом, . Таким образом, 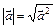 . .
Теорема. Скалярное произведение векторов  ( (  ) и ) и   , заданных в прямоугольной системе координат (О, , заданных в прямоугольной системе координат (О,  ), выражается формулой ), выражается формулой 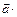  = =   . .
Условие перпендикулярности векторов  и и  : :
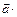  = 0, или в координатах: = 0, или в координатах:  . .
Косинус угла между ненулевыми векторами вычисляется по формуле:
сos (  , ,  )= )= 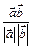 или сos ( или сos (  , ,  ) = ) =  . .
Примеры решения задач
1. Пусть АВСD — параллелограмм, О — точка пересечения диагоналей. Е, F — середины параллельных сторон ВС и АD. Построить на чертеже векторы:
 а) а)  . К . К
В С
А D
Рис. 2.6
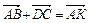 , где , где  (рис. 2.6). (рис. 2.6).
б)  . .
В Е С
А F D
Рис. 2.7
 (рис. 2.7). (рис. 2.7).
 в) в)  . В С . В С
О
А D
Рис. 2.8
 (рис. 2.8). (рис. 2.8).
г)  . .
 (рис. 2.9). (рис. 2.9).
В С
    
О
 А D А D
Рис. 2.9
д)  . .
 В Е С В Е С
О
А F D
Рис. 2.10
 (рис. 2.10). (рис. 2.10).
 е) е)  В Е С В Е С
О
А D
К
Рис. 2.11

=  где где 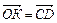 (рис. 11). (рис. 11).
2. По данным векторам  и и  построить вектор построить вектор  . .
Решение
Отложим векторы  и и  от одной точки (рис. 2.12): от одной точки (рис. 2.12):  . .
Построим  . По правилу параллелограмма . По правилу параллелограмма 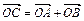 , поэтому , поэтому 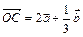 . .
 В С В С
В1
О А А1
Рис. 2.12
3.В ромбе ABCD (рис. 2.13) выразить векторы  через векторы через векторы  и и  . .
Решение
 
Рис. 2.13

4. Найти скалярное произведение векторов  и выяснить, являются ли они перпендикулярными. и выяснить, являются ли они перпендикулярными.
Решение
 , следовательно, векторы , следовательно, векторы  и и  перпендикулярны. перпендикулярны.
5.На плоскости даны векторы  (–1; 5), (–1; 5),  (3; 5), (3; 5), 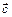 (–2; 8), (–2; 8),  (3; 1). Вычислить (3; 1). Вычислить 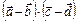 . .
Решение
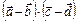 = ((–1; 5) – (3; 5))∙((–2; 8) –(3; 1)) = (–4; 0)∙(–5; 7) = = ((–1; 5) – (3; 5))∙((–2; 8) –(3; 1)) = (–4; 0)∙(–5; 7) =
=(–4)(–5) = 20.
6.Какой угол образуют единичные векторы  и и  , если известно, что векторы , если известно, что векторы   и и  перпендикулярны? перпендикулярны?
Решение
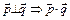 =0 =0  . Учитывая, что . Учитывая, что  , получим , получим
 . .
Таким образом, имеем  . .
§ 2. Деление отрезка в данном отношении.
Вычисление расстояния между точками.
Косое произведение векторов. Площадь треугольника
Если  , то , то  . .
 — формула для вычисления длины вектора — формула для вычисления длины вектора  или расстояния между точками М1 и М2. или расстояния между точками М1 и М2.
Определение. Точка М делит отрезок   в отношении в отношении  , причем , причем 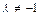 , если , если 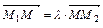 . .
Если  и М (х, у) точка делит отрезок М1М2 в отношении и М (х, у) точка делит отрезок М1М2 в отношении  , то , то
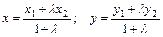 . . 
Для середины отрезка   . .
Определение. Косым произведением векторов  и и  называется произведение длин этих векторов на синус угла между ними, т. е. называется произведение длин этих векторов на синус угла между ними, т. е.  . .
Косое произведение в координатах вычисляется по формуле   = = 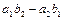 . .
Примеры решения задач
1. Найти точку М пересечения медиан треугольника АВС (рис. 2.14), если А(1; 4), В(–5; 0), С(–2; –1).
Решение
Рис. 2.14
D — середина BС 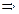  , ,  . .
Используя свойство медиан треугольника, получим 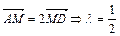 . Если М(х,у), то . Если М(х,у), то
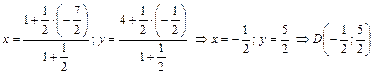 . .
2. Найти площадь треугольника АВС, если А(2;1), В(3;4) и С(1;6).
Решение
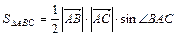 . Используя определение косого произведения векторов, получим, что . Используя определение косого произведения векторов, получим, что  . . 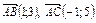 . .
 , следовательно, , следовательно, 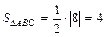 . .
§ 3. Различные способы задания прямой
Пусть d — некоторая прямая.
Определение. Каждый ненулевой вектор  , параллельный прямой d или лежащий на данной прямой, называется направляющим вектором этой прямой. , параллельный прямой d или лежащий на данной прямой, называется направляющим вектором этой прямой.
Уравнение прямой, заданной точкой
и направляющим векторому
M
M0
M1 
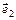
      O O  х х
Рис. 2.15
Прямая  d вполне определяется точкой d вполне определяется точкой  и направляющим вектором и направляющим вектором   || d (рис. 15). Так как || d (рис. 15). Так как  , где , где  , то уравнение прямой можно записать в виде , то уравнение прямой можно записать в виде
 , (1) , (1)
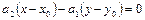 . (2) . (2)
 — каноническое уравнение (3) — каноническое уравнение (3)
Уравнения (1)—(3) — различные виды уравнений прямой 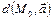 . .
Уравнение прямой, заданной двумя точками
Как известно, через две данные точки проходит единственная прямая. Найдем уравнение этой прямой. Пусть прямая задана двумя точками 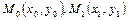 (рис. 2.15). Обозначим координаты произвольной точки М (х, у)Îd. В качестве направляющего вектора можно взять вектор (рис. 2.15). Обозначим координаты произвольной точки М (х, у)Îd. В качестве направляющего вектора можно взять вектор  и воспользоваться уравнениями (1) и (3). Запишем соответствующие уравнения: и воспользоваться уравнениями (1) и (3). Запишем соответствующие уравнения:
(4)  , ,
(5)  — каноническое уравнение прямой проходящей через две заданные точки. — каноническое уравнение прямой проходящей через две заданные точки.
Общее уравнение прямой
Различные формы записи уравнения прямой (1—5), рассмотренные нами в предыдущих пунктах параграфа, имеют в принципе один и тот же вид:
(6)  , ,
где А, В, С — некоторые числа.
Уравнение (6) называется общим уравнением прямой, где 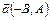 является направляющим вектором этой прямой. является направляющим вектором этой прямой.
Определение. Любой ненулевой вектор, перпендикулярный к данной прямой, называется вектором нормали данной прямой и обозначается  . Коэффициенты при переменных в общем уравнении прямой . Коэффициенты при переменных в общем уравнении прямой  являются координатами вектора нормали являются координатами вектора нормали 
Рассмотрим некоторые частные случаи уравнения (6):
1. Если С = 0, то уравнение принимает вид  и определяет прямую, проходящую через начало координат, так как ее координаты (0; 0) удовлетворяют этому уравнению (рис. 2.16) и определяет прямую, проходящую через начало координат, так как ее координаты (0; 0) удовлетворяют этому уравнению (рис. 2.16)

Рис. 2.16
2. Если В = 0 (А ¹ 0), то уравнение принимает вид  и определяет прямую, параллельную оси Оу (рис. 2.17). Это уравнение (при А ¹ 0) можно привести к виду и определяет прямую, параллельную оси Оу (рис. 2.17). Это уравнение (при А ¹ 0) можно привести к виду  или или 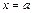 , где а — любое действительное число. В частности, если С = 0, то уравнение , где а — любое действительное число. В частности, если С = 0, то уравнение  определяет ось ординат. определяет ось ординат.
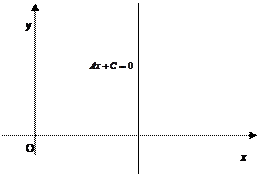
Рис. 2.17
3. Если А = 0 (В ¹ 0), то уравнение принимает вид  и определяет прямую, параллельную оси Ох (рис. 2.18). Это уравнение (при В ¹ 0) можно привести к виду и определяет прямую, параллельную оси Ох (рис. 2.18). Это уравнение (при В ¹ 0) можно привести к виду  или или 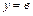 , где в — любое действительное число. В частности, если С = 0, то уравнение , где в — любое действительное число. В частности, если С = 0, то уравнение 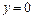 определяет ось абсцисс. определяет ось абсцисс.

Рис. 2.18
Не нашли, что искали? Воспользуйтесь поиском по сайту:
©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|







 х
х

 Обозначение:
Обозначение: 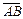 . А В
. А В
 называются одинаково (противоположно) направленными, если одинаково (противоположно) направлены лучи АВ и СD.
называются одинаково (противоположно) направленными, если одинаково (противоположно) направлены лучи АВ и СD. 
 и
и  называются одинаково (противоположно) направленными, если одинаково (противоположно) направлены какие-либо два представителя этих векторов.
называются одинаково (противоположно) направленными, если одинаково (противоположно) направлены какие-либо два представителя этих векторов. Направленный отрезок
Направленный отрезок  определяет вектор
определяет вектор 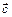 , который называется суммой векторов
, который называется суммой векторов  и
и 
 B
B  (рис. 2.2).
(рис. 2.2).
 (рис. 2.3).
(рис. 2.3). :
: — ассоциативность сложения.
— ассоциативность сложения. , что
, что  ,
,  .
. .
.
 (рис. 2.5).
(рис. 2.5).
 , удовлетворяющий условиям:
, удовлетворяющий условиям: ; 2.
; 2.  , если a ³ 0,
, если a ³ 0,  , если a < 0.
, если a < 0. и для любых действительных чисел a и b выполняются равенства:
и для любых действительных чисел a и b выполняются равенства: ; 2.
; 2.  ;
; ; 4.
; 4.  .
. и
и  . Векторы
. Векторы  .
.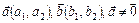 . Векторы
. Векторы  .
. разложения вектора
разложения вектора  в прямоугольной системе координат называются координатами вектора
в прямоугольной системе координат называются координатами вектора 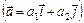 .
. .
. можно вычислить, зная координаты начала и конца этого вектора, т. е. если
можно вычислить, зная координаты начала и конца этого вектора, т. е. если  и
и  , то
, то  .
.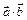 или
или  .
. ) в прямоугольной системе координат (О,
) в прямоугольной системе координат (О, 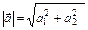 .
.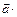
 называется скалярным квадратом вектора
называется скалярным квадратом вектора  . Таким образом,
. Таким образом, 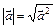 .
. ) и
) и  , заданных в прямоугольной системе координат (О,
, заданных в прямоугольной системе координат (О, 
 .
. .
.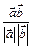 или сos (
или сos (  .
. а)
а)  . К
. К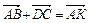 , где
, где  (рис. 2.6).
(рис. 2.6). .
.
 (рис. 2.7).
(рис. 2.7). в)
в)  . В С
. В С (рис. 2.8).
(рис. 2.8). .
. (рис. 2.9).
(рис. 2.9).




 А D
А D .
. В Е С
В Е С (рис. 2.10).
(рис. 2.10). е)
е)  В Е С
В Е С
 где
где 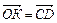 (рис. 11).
(рис. 11). .
. .
. . По правилу параллелограмма
. По правилу параллелограмма 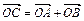 , поэтому
, поэтому 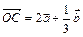 .
. В С
В С через векторы
через векторы  и
и  .
.


 и выяснить, являются ли они перпендикулярными.
и выяснить, являются ли они перпендикулярными. , следовательно, векторы
, следовательно, векторы  (3; 1). Вычислить
(3; 1). Вычислить 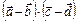 .
.
 и
и  перпендикулярны?
перпендикулярны?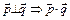 =0
=0  . Учитывая, что
. Учитывая, что  , получим
, получим .
. .
. , то
, то  .
. — формула для вычисления длины вектора
— формула для вычисления длины вектора  или расстояния между точками М1 и М2.
или расстояния между точками М1 и М2.
 в отношении
в отношении  , причем
, причем 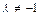 , если
, если 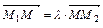 .
. и М (х, у) точка делит отрезок М1М2 в отношении
и М (х, у) точка делит отрезок М1М2 в отношении 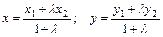 .
. 

 .
. .
.
 =
= 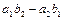 .
.
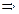
 ,
,  .
.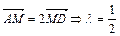 . Если М(х,у), то
. Если М(х,у), то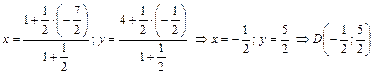 .
.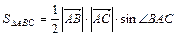 . Используя определение косого произведения векторов, получим, что
. Используя определение косого произведения векторов, получим, что  .
. 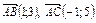 .
. , следовательно,
, следовательно, 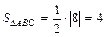 .
.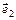
 d вполне определяется точкой
d вполне определяется точкой  и направляющим вектором
и направляющим вектором  || d (рис. 15). Так как
|| d (рис. 15). Так как  , где
, где  , то уравнение прямой можно записать в виде
, то уравнение прямой можно записать в виде , (1)
, (1)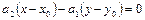 . (2)
. (2) — каноническое уравнение (3)
— каноническое уравнение (3)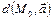 .
.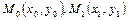 (рис. 2.15). Обозначим координаты произвольной точки М (х, у)Îd. В качестве направляющего вектора можно взять вектор
(рис. 2.15). Обозначим координаты произвольной точки М (х, у)Îd. В качестве направляющего вектора можно взять вектор  и воспользоваться уравнениями (1) и (3). Запишем соответствующие уравнения:
и воспользоваться уравнениями (1) и (3). Запишем соответствующие уравнения: ,
, — каноническое уравнение прямой проходящей через две заданные точки.
— каноническое уравнение прямой проходящей через две заданные точки. ,
,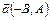 является направляющим вектором этой прямой.
является направляющим вектором этой прямой. . Коэффициенты при переменных в общем уравнении прямой
. Коэффициенты при переменных в общем уравнении прямой  являются координатами вектора нормали
являются координатами вектора нормали 
 и определяет прямую, проходящую через начало координат, так как ее координаты (0; 0) удовлетворяют этому уравнению (рис. 2.16)
и определяет прямую, проходящую через начало координат, так как ее координаты (0; 0) удовлетворяют этому уравнению (рис. 2.16)
 и определяет прямую, параллельную оси Оу (рис. 2.17). Это уравнение (при А ¹ 0) можно привести к виду
и определяет прямую, параллельную оси Оу (рис. 2.17). Это уравнение (при А ¹ 0) можно привести к виду  или
или 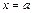 , где а — любое действительное число. В частности, если С = 0, то уравнение
, где а — любое действительное число. В частности, если С = 0, то уравнение  определяет ось ординат.
определяет ось ординат.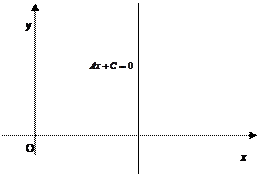
 и определяет прямую, параллельную оси Ох (рис. 2.18). Это уравнение (при В ¹ 0) можно привести к виду
и определяет прямую, параллельную оси Ох (рис. 2.18). Это уравнение (при В ¹ 0) можно привести к виду  или
или 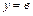 , где в — любое действительное число. В частности, если С = 0, то уравнение
, где в — любое действительное число. В частности, если С = 0, то уравнение 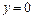 определяет ось абсцисс.
определяет ось абсцисс.