
|
|
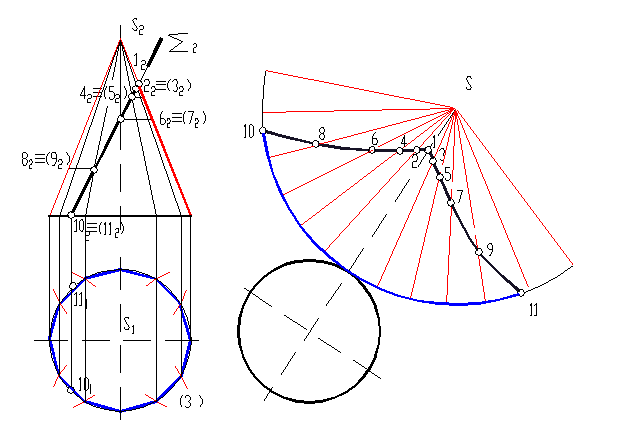
Развертка прямого кругового конуса12 Полная развертка прямого кругового конуса представляет собой сектор, радиус которого равен образующей конуса, а длина дуги равна длине окружности основания конуса и пристроенный к нему круг основания. Для получения приближенной развертки конической поверхности, усеченной фронтально проецирующей плоскостью, заменяем последнюю на вписанную в нее 12-ти угольную правильную пирамиду (рисунок 17). Для этого делим окружность основания конуса своим радиусом на 12 частей . Через эти точки деления проводим соответственно 12 образующих конуса. Точка 1 принадлежит правой очерковой образующей конуса, проецирующейся на П2 в натуральную величину, т.к. она является фронтальной прямой уровня, поэтому на развертке расстояние от вершины S до точки 1 равно отрезку S212. Для определения расстояний от вершины S до остальных точек пересечения образующих конуса с секущей плоскостью проводим через их фронтальные проекции прямые, параллельные фронтальной проекции основания конуса, до пересечения с одной из очерковых (правой или левой) образующих конуса. Это соответствует вращению этих образующих до положения, параллельного плоскости П2. Точки 10 и 11, лежащие на очерке основания конуса, находим измеряя наименьшую хорду по дуге окружности.
Рисунок 17
Примеры решения задач
Рисунок 18
1. Построить три проекции геометрического тела и линию пересечения его поверхности с плоскостью S. 2. Найти натуральную величину фигуры полученной в пересечении. 3. Построить полную развертку усеченной части геометрического тела. 4. Из чертежной бумаги выполнить модель усеченной части геометрического тела.
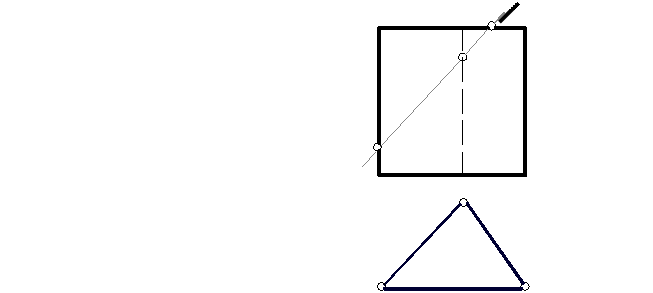
Алгоритм решения 1. Строим три проекции призмы. 2. Находим линию пересечения секущей плоскости с поверхностью призмы. При пересечении призмы с плоскостью S (S2) в данном случае получается 4-х угольник, вершинами которого являются точки пересечения секущей плоскости с ребрами и верхним основанием призмы, а именно, при пересечении плоскости S (S2) с ребром А (А2) получаем точку 1 (12), с ребром В (В2) – точку 2 (22) и в пересечении с верхним основанием - точки 3 и 4 í(32) º (42)ý. Находим недостающие проекции точек, используя свойства поверхности и методы нахождения точек на них. Соединяем полученные точки между собой последовательно и с учетом видимости. 3. Определяем натуральную величину фигуры, полученной в пересечении плоскости S с призмой методом вращения. В качестве оси вращения выбираем фронтально проецирующую прямую i, проходящую через точку 1. Фронтальные проекции точек 1, 2, 3, 4 будут перемещаться по окружностям и займут положение, соответственно, 4. Строим полную развертку усеченной части призмы. (Построение разверток геометрических тел описано выше). Для построения полной развертки усеченной части призмы необходимо найти на развертке точки 1, 2, 3 и 4, последовательно их соединить и пристроить нижнее основание, часть верхнего основания и натуральную величину фигуры сечения. 5. Склеиваем из чертежной бумаги модель усеченной части конуса с призматическим отверстием.
На рисунке 23 приведен пример выполнения задачи 1.
Построить три проекции конуса с вырезом. Рисунок 18 Алгоритм решения
1. Строим три проекции конуса в тонких линиях (рисунок 19). 2. Определяем, каким количеством плоскостей образован вырез, и какая фигура получается в пересечении поверхности с этими плоскостями. В данном примере вырез образован 3-мя плоскостями: плоскость S (S2) в пересечении с конусом дает параболу, плоскость Y (Y2) – гиперболу, а плоскость Г (Г2) – окружность.
Рисунок 19 3. Определяем точки пересечения секущих плоскостей с характерными (очерковыми) образующими конуса – 1(12), 2,3 (22 º 32), 8,9 (82 º 92), 10 (102); точки пересечения плоскостей между собой 4, 5, 6, 7 (42 º 52) и (62 º 72). Кроме этих точек определяем промежуточные точки для построения параболы и гиперболы. 4. Находим горизонтальные и профильные проекции названных точек методом секущих плоскостей. 5. Соединяем последовательно полученные точки с учетом видимости. Т.к. на горизонтальной проекции видны все точки, лежащие на боковой поверхности конуса, то соединяем линией видимого контура точки 11– 21– 41 и 11– 31– 51 (ветви параболы); 41– 61 и 51– 71 (ветви гиперболы); 61– 81– 101 и 71– 91– 101 (части окружности). Между точками 41– 51 и 61– 71 проводим линии невидимого контура, которые получаются за счет пересечения плоскостей S и Y и Y и Г. На профильной проекции видимыми будут все линии пересечения: 13– 23– 43 и 13– 23– 43 (ветви параболы), 43– 63 и 53 – 73 (ветви гиперболы), линия 83– 103– 93, в которую проецируется окружность, а также линия пересечения плоскостей S и Y 43– 53. 6. На профильной плоскости проекции обводим очерк конуса: левую и правую очерковые образующие соответственно – от вершины до точек 33 и 23 и от точек 93 и 83 до линии основания. Задача 3 (Рисунок 20а) (Построить три проекции прямого кругового цилиндра и найти недостающие проекции заданных точек, лежащих на его поверхности)
а) б) Рисунок 20 Алгоритм решения
Строим три проекции цилиндра Находим недостающие проекции заданных точек, используя свойства цилиндрической поверхности: все точки и линии, лежащие на боковой поверхности цилиндра, на горизонтальной проекции располагаются на дуге окружности основания. Т.к. точка 1(12) расположена на правой очерковой образующей цилиндра В (В2), которая на П1 проецируется в точку В1 (прямая горизонтально проецирующая), то и горизонтальная проекция точки 1 (11) совпадает с проекцией этой образующей. Аналогичным образом находим горизонтальную проекцию точки 2, расположенной на дальней образующей цилиндра. Горизонтальную проекцию точки 3, расположенной на боковой поверхности цилиндра, находим на пересечении вертикальной линии связи из точки 32 и дуги окружности основания.
Рисунок 21 Профильные проекции точек 1(13) и 2(23) находим на пересечении горизонтальных линий связи, проведенных, соответственно, из точек 12 и 22 и образующих В(В3) и D(D3). Для построения профильной проекции точки 3(33) замеряем расстояние от базовой плоскости Ф1 до точки 31 и откладываем его от Ф3 по горизонтальной линии связи, проведенной из точки 32. Т.к. на горизонтальной проекции видны только точки, лежащие на верхнем основании, то точка 4, заданная невидимой, принадлежит нижнему основанию, а точка 5, по заданию видимая, расположена на верхнем основании. На П2 проекции этих точек находим на пересечении вертикальных линий связи, проведенных из заданных горизонтальных проекций точек 41 и 51 с линиями нижнего и верхнего оснований. Профильные проекции точек 4(43) и 5(53) находим замеряя расстояния от базовой плоскости Ф1 до точек 41 и 51 и откладывая их от Ф3, соответственно, по линии нижнего и верхнего оснований.
Задача 4 (Рисунок 20б) (Построить три проекции треугольной пирамиды и найти недостающие проекции заданных точек, лежащих на ее поверхности)
Алгоритм решения
Строим три проекции пирамиды, используя для построения профильной проекции базовую плоскость Ф, проведенную через точку А.
Рисунок 22
По заданным проекциям точек находим их недостающие проекции. Находим горизонтальную и профильную проекции точки 1 (11 и 13) на пересечении горизонтальной и вертикальной линий связи, проведенных из точки 12 с проекциями ребра AS (A1S1 и A3S3). Точка 2 задана на ребре SB. Горизонтальную проекцию точки 2(21) находим методом секущей плоскости: через заданную проекцию точки 22 проводим горизонтальную плоскость уровня Г(Г2), которая в пересечении с поверхностью пирамиды дает треугольник подобный основанию. Строим горизонтальную проекцию этого треугольника через вспомогательные точки, расположенные на ребрах AS (A2S2) CS(C2S2). На пересечении вершины построенного треугольника и ребра SB найдем горизонтальную проекцию точки 2(21). Профильную проекцию точки 2(23) найдем на пересечении горизонтальной линии связи, проведенной из точки 22 и ребра SB (S2B2). Недостающие проекции точек 5 (52) и 3 (31) находим методом образующей: через вершину S и заданные проекции точек проводим прямую линию (образующую) до пересечения со стороной основания, строим проекции этих образующих и на них находим искомые проекции точек. Профильные проекции точек 5(53) и 3(33) находим замеряя расстояния от базовой плоскости Ф1 до точек 51 и 31 и откладывая их от Ф3 по горизонтальным линиям связи, проведенным из точек 52 и 32. Т.к. точка 4(41) задана невидимой, значит она расположена на основании пирамиды и для ее нахождения на П2 достаточно провести вертикальную линию связи до пересечения с линией основания, а на П3 – замерить расстояние от базовой плоскости Ф(Ф1) до горизонтальной проекции точки 4(41) и отложить его на П3 по линии основания.
Контрольные вопросы
1. Что называется многогранником? 2. Что является сечением поверхности многогранника плоскостью? 3. Какие способы построения сечения многогранника плоскостью существуют? В чем заключаются эти способы? 4. Как формируется алгоритм построения точек пересечения прямой с поверхностью многогранника? 5. Что называется поверхностью вращения? 6. Укажите основные свойства поверхностей вращения. 7. Какие линии на поверхности вращения называются: параллелью, экватором, горлом, меридианом, главным меридианом? 8. Какие фигуры могут быть получены при рассечении плоскостью кругового цилиндра, конуса, сферы? В каких случаях эти поверхности рассекутся по графически простым линиям? 9. Назовите методы нахождения точек на поверхностях вращения. 10. Какие точки линии пересечения поверхности с плоскостью называются опорными, промежуточными? 11. Сформулируйте алгоритм нахождения точек пересечения прямой с поверхностью вращения. 12. Как строятся развертки многогранных поверхностей (призмы и пирамиды)? 13. Как строятся развертки поверхностей вращения (цилиндра, конуса, сферы)?
Рисунок 23 - Пример выполнения листа 1 задания 4
Рисунок 24 – Пример выполнения листа 2 задания 4 Задание 4 «Пересечение поверхностей» Целевое назначение Закрепить знания студентов о способах построения линий пересечения поверхностей.
Содержание задания Задание состоит из двух задач, требующих построения линии взаимного пересечения двух поверхностей. В первой задаче пересекаются многогранник с поверхностью вращения, во второй – две поверхности вращения. Указания к выполнению задания Каждая задача задания выполняется в трех проекциях на отдельном формате чертежной бумаги формата А3 в масштабе 1:1 по номеру своего варианта заданий. Размеры на чертежах не проставлять. Секущие плоскости и линии проекционной связи проводятся тонкими сплошными линиями. Линии, определяющие полный очерк геометрической поверхности в местах наложения проекций, показываются сплошной тонкой линией. Плоскости надо обозначать прописными буквами греческого алфавита, а точки линии пересечения арабскими цифрами. При решении задач проводят большое число секущих плоскостей для лучшего определения характера линии пересечения. Но в окончательной обводке чертежа рекомендуется сохранить лишь те, которые определяют опорные точки и несколько промежуточных. Для этих точек на чертеже должны быть полностью сохранены линии построения и линии проекционной связи. Перед выполнением задания необходимо изучить теоретический материал по заданной теме и ответить на контрольные вопросы. На рисунках 27 и 28 приведены примеры выполнения задания.
Примеры решения задач Задача 1 (Рисунок 25) Построить линию пересечения призмы и конуса.
Рисунок 25
Алгоритм решения
Плоскость каждой грани призмы в пересечении с поверхностью конуса дает свой тип линий - это будут плоские кривые второго порядка: грань АВ – часть эллипса, грань ВС – часть параболы, грань АС – часть окружности. Эти три кривые соединяются между собой в замкнутую кривую. Для построения линии пересечения используется метод секущих плоскостей. В качестве секущих плоскостей используются горизонтальные плоскости уровня (Г, Г¢, Г¢¢…). Эти плоскости в пересечении с призмой дают прямоугольники, а с конусом – окружности. В пересечении окружностей с соответствующими прямоугольниками получаем точки искомой линии пересечения. Следует учесть, что если в пересечении участвует проецирующая поверхность (призма или цилиндр), то линия пересечения на одной из проекций известна сразу: она совпадает с проекцией основания проецирующей поверхности. В данном примере фронтальная проекция линии пересечения совпадает с фронтальной проекцией очерка основания призмы. 1. Построение начинаем с обозначения характерных (опорных) точек линии пересечения. В первую очередь определяем точки пересечения ребер призмы с поверхностью конуса (12, 22, 32, 42, 52), затем точки пересечения очерковых образующих конуса с гранями призмы (62, 72, 82, 92). 2. Определяем количество и место положения промежуточных точек. Число промежуточных точек должно быть достаточным для точного построения эллипса и параболы. Для построения окружности промежуточные точки не требуются. Чтобы не загромождать чертеж, промежуточные точки допускается цифрами не обозначать. 3. Находим горизонтальные проекции выбранных точек. Горизонтальная проекция точки 1 (11) находится в пересечении ребра А с левой очерковой образующей конуса. Для нахождения горизонтальных проекций точек 2(21) и 3 (31) вводим секущую плоскость Г (Г2), которая рассекает конус по окружности радиуса R. Фронтальная проекция окружности совпадает с линией плоскости, а на горизонтальной проекции окружность проецируется в натуральную величину. В пересечении этой окружности с ребром В получаем горизонтальные проекции точек 2 (21) и 3 (31). Аналогичным образом строим все остальные точки, последовательно вводя плоскости Г¢, Г¢¢…. 4. По двум имеющимся проекциям точек строим их профильные проекции, последовательно соединив которые, получим профильную проекцию линии пересечения. 5. Видимость линии пересечения на горизонтальной проекции определяем по призме, т.е. линия пересечения, лежащая на видимых гранях АВ (часть эллипса) и ВС (часть параболы) будет видна, а часть окружности, принадлежащая грани АС – не видна и изображается линией невидимого контура. Обводим очерки поверхностей. У призмы ребро А(А1) полностью видимое, а ребра В(В1) и С(С1) видны соответственно до точек 2(21),3(31) и 4(41), 5(51). Часть основания конуса, расположенного под призмой, не видна и изображается линией невидимого контура. 6. Видимость линии пересечения на профильной проекции определяем по конусу. Границей видимости линии пересечения являются точки 6(63) и 7(73). Часть эллипса от точки 1(13) до точек 6(63) и 7(73) будет видна, а далее до точек 2(23) и 3(33) не видна. Ветви параболы, лежащие на грани ВС – не видны. Часть окружности линии пересечения совпадает с проекцией видимого на профильной проекции ребра призмы А(А3). Ребро призмы В(В3) существует до точек 2(23) и 3(33), и часть его (за конусом) до этих точек будет невидимым. Очерковые образующие конуса существуют и видны до точек 6(63) и 7(73) и от точек 8(83) и 9(93) до основания конуса.
Задача 2 (Рисунок 26) Построить линию пересечения шара и конуса.
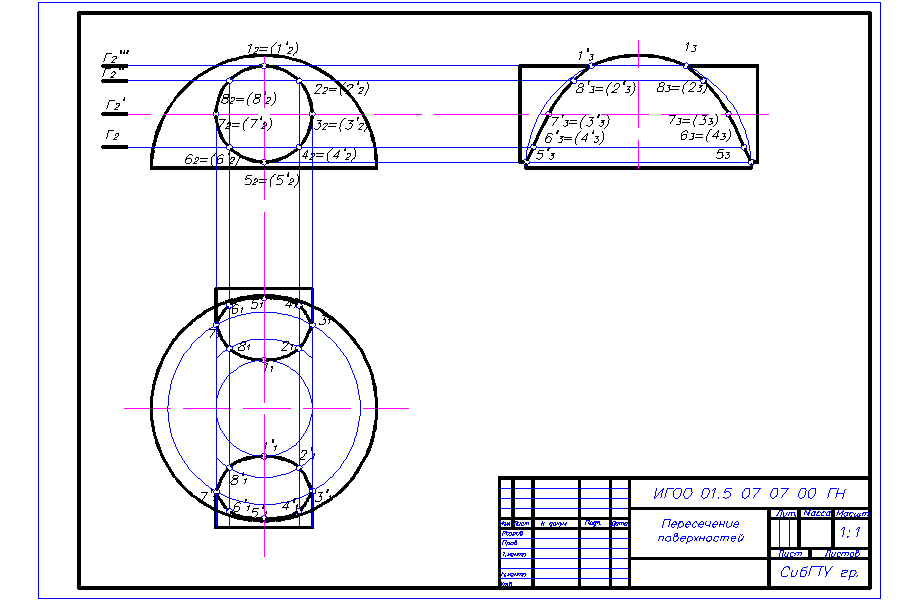
Алгоритм решения Задача решается способом секущих плоскостей. В нашем примере для построения линии пересечения рационально использовать горизонтальные плоскости уровня. Они рассекут конус и шар по окружностям, которые на плоскости П1 изображаются без искажения. 1. Граница проведения секущих плоскостей определяется точками 1 и 2 (12 и 22), высшей и низшей точками линии пересечения. Первую секущую плоскость Г проведем через экватор шара. Она рассечет шар по окружности с радиусом R , а конус по окружности с радиусом R1. 2. Строим горизонтальную проекцию сечения конуса. (Горизонтальная проекция сечения шара плоскостью Г совпадает с проекцией экватора). В пересечении контуров этих сечений (окружностей) получим горизонтальные проекции точек 31 и 41 линии пересечения. Эти точки одновременно являются и опорными. Они на горизонтальной проекции отделяют видимую часть линии пересечения от не видимой, т.к. лежат на экваторе шара. Фронтальные проекции этих точек находятся на плоскости Г (Г2). 3. Для построения промежуточных точек в пределах высшей (12) и низшей (22) точек линии пересечения проводим целый ряд секущих плоскостей (Г2¢, Г¢¢2…), строим их сечения, в пересечении которых определяются искомые точки. В нашем примере построена лишь одна пара промежуточных точек. 4. Плавной кривой соединяем эти точки. Окончательную обводку делаем по лекалу. 5. На проекциях линии пересечения отмечаем точки 5, 6, 7 и 8 пересечения ближней и дальней образующей конуса с поверхностью шара, а также точки 9 и 10 пересечения второго главного меридиана сферы с поверхностью конуса, которые также являются опорными. 6. Видимость линии пересечения на горизонтальной и профильной проекции определяем по сфере. На горизонтальной проекции линия пересечения видна от точки 1(11) до точек 3(31) и 4(41), а далее от этих точек до точки 2(21) не видимая. Часть основания конуса (под сферой) изображается линией невидимого контура. На профильной плоскости проекций линия пересечения видна только от точки 1(13) до точек 9(93) и 10(103). Очерковый второй главный меридиан сферы обводим линией видимого контура от наивысшей точки до точек 9(93) и 10(103). Очерковые образующие конуса существуют от вершины S(S3) до точек 5(53) и 6(63) и от основания до точек 7(73) и 8(83). Часть образующих конуса (за сферой) изображаем линиями невидимого контура.
Контрольные вопросы
1. Сформулируйте правило построения линии взаимного пересечения поверхностей многогранников. 2. Сформулируйте правило построения линии взаимного пересечения многогранника с поверхностью вращения. 3. Сформулируйте правило построения линии взаимного пересечения поверхностей вращения. 4. Сущность метода вспомогательных плоскостей.
Рисунок 27 – Пример выполнения листа 1 задания 5
Рисунок 28 – Пример выполнения листа2 задания 5 ПРИЛОЖЕНИЯ (варианты задач к заданиям) Задание 01.1 «Точка. Прямая»
Вариант 1 Задана прямая АВ координатами точек: А /145,25,50/ , B /25,95,90/. 1. Построить точку С, расположенную относительно точки А правее на 50мм, дальше на 15мм, и выше на 30 мм. 2. Построить точку D, расположенную относительно точки С правее на 60мм, ближе на 25мм и ниже на 50мм. 3. Через точку D провести прямую DF, параллельную прямой АВ. 4. Через точку С провести прямую СЕ, параллельную плоскости П 5. Определить взаимное положение прямых АВ и СD и доказать это на чертеже. 6. Разделить прямую АВ точкой К в отношении АК:КВ=3:2. 7.Пересечь прямую АВ горизонтально-проецирующей прямой MN. Координаты точек Е , F, M, M взять произвольно.
Вариант 2 Задана прямая АВ координатами точек: А /160,90,95/ , B /40,50,25/. 1. Построить точку С, расположенную относительно точки А правее на 70мм, ближе на 10мм, и ниже на 55 мм. 2. Построить точку D, расположенную относительно точки С левее на 60мм, ближе на 50мм и ниже на 25мм. 3. Через точку D провести прямую DF, параллельную прямой АВ. 4. Через точку С провести прямую СЕ, параллельную плоскости П 5. Определить взаимное положение прямых АВ и СD и доказать это на чертеже. 6. Разделить прямую АВ точкой К в отношении АК:КВ=2:1. 7.Пересечь прямую АВ фронтально-проецирующей прямой MN. Координаты точек Е , F, M, M взять произвольно. Вариант 3 1. Построить проекции пересекающихся прямых АВ и СD, заданных координатами точек: А /130,80,60/, B /30,60,100/ . Точка С расположена относительно точки А правее на 80мм, ближе на 40мм, выше на 5мм. D /150,30, ? /. Найти недостающую координату точки D и записать ее. 2. Через точку D провести прямую DF, параллельную прямой АВ. 3. Через точку С провести прямую СЕ, параллельную плоскости П и пересекающую прямую АВ. Назвать эту прямую и записать ее натуральную величину. 4. Разделить прямую АВ точкой К в отношении АК:КВ=3:2. 5.Пересечь прямую АВ горизонтально-проецирующей прямой MN. Координаты точек Е , F, M, M взять произвольно. Вариант 4 Задана прямая АВ координатами точек: А /180,25,35/ , B /40,110,80/. 1. Построить точку С, расположенную относительно точки А правее на 70мм, ближе на 60мм, и ниже на 25 мм. 2. Построить точку D, расположенную относительно точки С правее на 70мм, дальше на 60мм и выше на 65мм. 3. Через точку С провести прямую СF, параллельную прямой АВ. 4. Через точку С провести прямую СЕ, параллельную плоскости П натуральную величину. 5. Определить взаимное положение прямых АВ и СD и доказать это на чертеже. 6. Разделить прямую АВ точкой К в отношении АК:КВ=5:2. 7.Пересечь прямую АВ фронтально-проецирующей прямой MN. Координаты точек Е , F, M, M взять произвольно. Вариант 5 1. Построить проекции пересекающихся прямых АВ и СD, заданных координатами точек: А /140,45,25/, B /80,105,95/ . Точка С расположена относительно точки А правее на 105мм, дальше на 40мм, выше на 10мм. D /155, ?,40 /. Найти недостающую координату точки D и записать ее. 2. Через точку D провести прямую DF, параллельную прямой АВ. 3. Через точку С провести прямую СЕ, параллельную плоскости П пересекающую прямую АВ. Назвать эту прямую и записать ее натуральную величину. 4. Разделить прямую АВ точкой К в отношении АК:КВ=4:3. 5.Пересечь прямую АВ горизонтально-проецирующей прямой MN. Координаты точек Е , F, M, M взять произвольно.
Вариант 6 1. Построить проекции пересекающихся прямых АВ и СD, заданных координатами точек: А /165,80,105/, B /30,35,25/ . Точка С расположена относительно точки А правее на 40мм, ближе на 60мм, ниже на 105мм. D /90, ?, 90 /. Найти недостающую координату точки D и записать ее. 2. Через точку D провести прямую DF, параллельную прямой АВ. 3. Через точку С провести прямую СЕ, параллельную плоскости П натуральную величину. 4. Разделить прямую АВ точкой К в отношении АК:КВ=3:4. 5.Пересечь прямую АВ фронтально-проецирующей прямой MN. Координаты точек Е , F, M, M взять произвольно. Вариант 7 Задана прямая АВ координатами точек: А /70,85,80/ , B /170,50,35/. 1. Построить точку С, расположенную относительно точки А левее на 35мм, ближе на 85мм, и ниже на 75 мм. 2. Построить точку D, расположенную относительно точки В правее на 40мм, дальше на 30мм и выше на 35мм. 3. Через точку С провести прямую СF, параллельную прямой АВ. 4. Через точку D провести прямую DЕ, параллельную плоскости П и пересекающую прямую АВ. Назвать эту прямую и записать ее натуральную величину. 5. Определить взаимное положение прямых АВ и СD и доказать это на чертеже. 6. Разделить прямую АВ точкой К в отношении АК:КВ=4:1. 7.Пересечь прямую АВ горизонтально-проецирующей прямой MN. Координаты точек Е , F, M, M взять произвольно.
Вариант 8 Задана прямая АВ координатами точек: А /145,10,75/ , B /45,35,25/. 1. Построить точку С, расположенную относительно точки А правее на 5мм, ближе на 80мм, и ниже на 55 мм. 2. Построить точку D, расположенную относительно точки В левее на 10мм, ближе на 20мм и выше на 35мм. 3. Через точку С провести прямую СF, параллельную прямой АВ. 4. Через точку D провести прямую DЕ, параллельную плоскости П и пересекающую прямую АВ. Назвать эту прямую и записать ее натуральную величину. 5. Определить взаимное положение прямых АВ и СD и доказать это на чертеже. 6. Разделить прямую АВ точкой К в отношении АК:КВ=2:3. 7.Пересечь прямую АВ фронтально-проецирующей прямой MN. Координаты точек Е , F, M, M взять произвольно.
Вариант 9 Задана прямая АВ координатами точек: А /150,90,60/ , B /15,30,10/. 1. Построить точку С, расположенную относительно точки А правее на 75мм, дальше на 10мм и ниже на 45 мм. 2. Построить точку D, расположенную относительно точки В левее на 120мм, дальше на 5мм и выше на 80мм. 3. Через точку D провести прямую DF, параллельную прямой АВ. 4. Через точку С провести прямую СЕ, параллельную плоскости П и пересекающую прямую АВ. Назвать эту прямую и записать ее натуральную величину. 5. Определить взаимное положение прямых АВ и СD и доказать это на чертеже. 6. Разделить прямую АВ точкой К в отношении АК:КВ=3:5. 7.Пересечь прямую АВ горизонтально-проецирующей прямой MN. Координаты точек Е , F, M, M взять произвольно. Вариант 10 Задана прямая АВ координатами точек: А /150,5,45/ , B /25,55,115/. 1. Построить точку С, расположенную относительно точки А правее на 45мм, ближе на 45мм, и ниже на 35 мм. 2. Построить точку D, расположенную относительно точки В левее на 25мм, дальше на 35мм и выше на 35мм. 3. Через точку D провести прямую DF, параллельную прямой АВ. 4. Через точку C провести прямую CЕ, параллельную плоскости П и пересекающую прямую АВ. Назвать эту прямую и записать ее натуральную величину. 5. Определить взаимное положение прямых АВ и СD и доказать это на чертеже. 6. 7.Пересечь прямую АВ фронтально-проецирующей прямой MN. Координаты точек Е , F, M, M взять произвольно. Вариант 11 Задана прямая АВ координатами точек: А /160,65,95/ , B /40,50,20/. 1. Построить точку С, расположенную относительно точки В левее на 110мм, дальше на 45мм, и выше на 40 мм. 2. Построить точку D, расположенную относительно точки А правее на 55мм, ближе на 15мм и ниже на 85мм. 3. Через точку D провести прямую DF, параллельную прямой АВ. 4. Через точку С провести прямую СЕ, параллельную плоскости П и пересекающую прямую АВ. Назвать эту прямую и записать ее натуральную величину. 5. Определить взаимное положение прямых АВ и СD и доказать это на чертеже. 6. Разделить прямую АВ точкой К в отношении АК:КВ=4:1. 7.Пересечь прямую АВ горизонтально-проецирующей прямой MN. Координаты точек Е , F, M, M взять произвольно.
Вариант 12 1. Построить проекции пересекающихся прямых АВ и СD, заданных координатами точек: А /125,95,120/, B /25,60,45/ . Точка С расположена относительно точки А левее на 35мм, дальше на 30мм, ниже на 40мм. D /65,105, ? /. Найти недостающую координату точки D и записать ее. 2. Через точку D провести прямую DF, параллельную прямой АВ. 3. Через точку С провести прямую СЕ, параллельную плоскости П пересекающую прямую АВ. Назвать эту прямую и записать ее натуральную величину. 4. Разделить прямую АВ точкой К в отношении АК:КВ=2:3. 5.Пересечь прямую АВ фронтально-проецирующей прямой MN. Координаты точек Е , F, M, M взять произвольно. Вариант 13 1. Построить проекции пересекающихся прямых АВ и СD, заданных координатами точек: А /75,10,40/, B /130,105,100/ . Точка С расположена относительно точки А ближе на 50мм и выше на 50мм. D /135,40, ? /. Найти недостающую координату точки D и записать ее. 2. Через точку D провести прямую DF, параллельную прямой АВ. 3. Через точку С провести прямую СЕ, параллельную плоскости П пересекающую прямую АВ. Назвать эту прямую и записать ее натуральную величину. 4. Разделить прямую АВ точкой К в отношении АК:КВ=3:2. 5.Пересечь прямую АВ горизонтально-проецирующей прямой MN. Координаты точек Е , F, M, M взять произвольно.
Вариант 14 Задана прямая АВ координатами точек: А /165,65,95/ , B /40,20,15/. 1. Построить точку С, расположенную относительно точки А правее на 35мм, дальше на 25мм и ниже на 65 мм. 2. Построить точку D, расположенную относительно точки В левее на 30мм, ближе на 5мм и выше на 65мм. 3. Через точку D провести прямую DF, параллельную прямой АВ. 4. Через точку С провести прямую СЕ, параллельную плоскости П и пересекающую прямую АВ. Назвать эту прямую и записать ее натуральную величину. 5. Определить взаимное положение прямых АВ и СD и доказать это на чертеже. 6. Разделить прямую АВ точкой К в отношении АК:КВ=1:3. 7.Пересечь прямую АВ фронтально-проецирующей прямой MN. Координаты точек Е , F, M, M взять произвольно. Вариант 15 Задана прямая АВ координатами точек: А /125,105,100/ , B /20,15,25/. 1. Построить точку С, расположенную относительно точки А левее на 5мм, дальше на 65мм и ниже на 70 мм. 2. Построить точку D, расположенную относительно точки В левее на 20мм, ближе на 60мм и ниже на 10мм. 3. Через точку D провести прямую DF, параллельную прямой АВ. 4. Через точку С провести прямую СЕ, параллельную плоскости П и пересекающую прямую АВ. Назвать эту прямую и записать ее натуральную величину. 5. Определить взаимное положение прямых АВ и СD и доказать это на чертеже. 6. Разделить прямую АВ точкой К в отношении АК:КВ=5:2. 7.Пересечь прямую АВ горизонтально-проецирующей прямой MN. Координаты точек Е , F, M, M взять произвольно.
Вариант 16 Задана прямая АВ координатами точек: А /150,90,60/ , B /15,30,10/. 1. Построить точку С, расположенную относительно точки А правее на 75мм, дальше на 10мм и ниже на 45 мм. 2. Построить точку D, расположенную относительно точки В левее на 120мм, дальше на 5мм и выше на 80мм. 3. Через точку D провести прямую DF, параллельную прямой АВ. 4. Через точку С провести прямую СЕ, параллельную плоскости П и пересекающую прямую АВ. Назвать эту прямую и записать ее натуральную величину. 5. Определить взаимное положение прямых АВ и СD и доказать это на чертеже. 6. Разделить прямую АВ точкой К в отношении АК:КВ=3:5. 7.Пересечь прямую АВ фронтально-проецирующей прямой MN. Координаты точек Е , F, M, M взять произвольно. Вариант 17 Задана прямая CD координатами точек: C /145,25,50/ , D /25,95,90/. 1. Построить точку A, расположенную относительно точки C правее на 110мм, ближе на 10мм и ниже на 20 мм. 2. Построить точку B, расположенную относительно точки D левее на 60мм, дальше на 25мм и выше на 10мм. 3. Через точку D провести прямую DF, параллельную прямой АВ. 4. Через точку A провести прямую AЕ, параллельную плоскости П и пересекающую прямую CD. Назвать эту прямую и записать ее натуральную величину. 5. Определить взаимное положение прямых АВ и СD и доказать это на чертеже. 6. Разделить прямую CD точкой К в отношении CК:КD=1:4. 7.Пересечь прямую АВ горизонтально-проецирующей прямой MN. Координаты точек Е , F, M, M взять произвольно. Вариант 18 Задана прямая CD координатами точек: C/40,50,25/ , D /160,90,95/. 1. Построить точку A, расположенную относительно точки C левее на 50мм, дальше на 30мм и выше на 55 мм. 2. Построить точку B, расположенную относительно точки A левее на 60мм, ближе на 100мм и ниже на 80мм. 3. Через точку B провести прямую BF, параллельную прямой CD. 4. Через точку A провести прямую AЕ, параллельную плоскости П и пересекающую прямую CD. Назвать эту прямую и записать ее натуральную величину. 
12 Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
 2,
2,  2,
2,  2, и
2, и  2 , а горизонтальные проекции – по прямым, перпендикулярным оси вращения i (i1) и вертикальным линиям связи, в пересечении с которыми получим новое положение точек
2 , а горизонтальные проекции – по прямым, перпендикулярным оси вращения i (i1) и вертикальным линиям связи, в пересечении с которыми получим новое положение точек  Задача 2 (Рисунок 18)
Задача 2 (Рисунок 18)

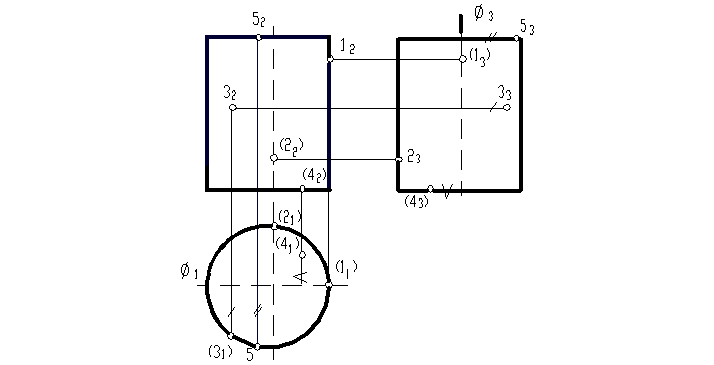
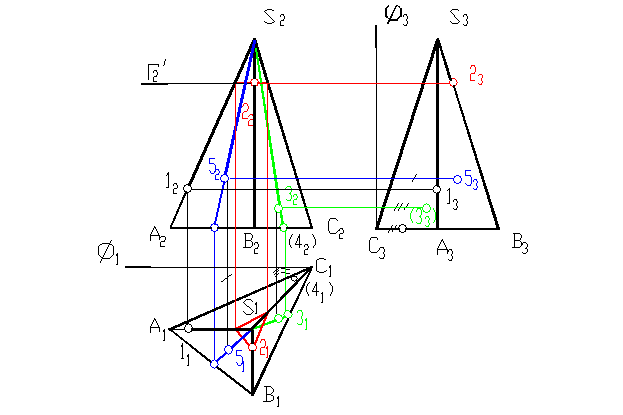
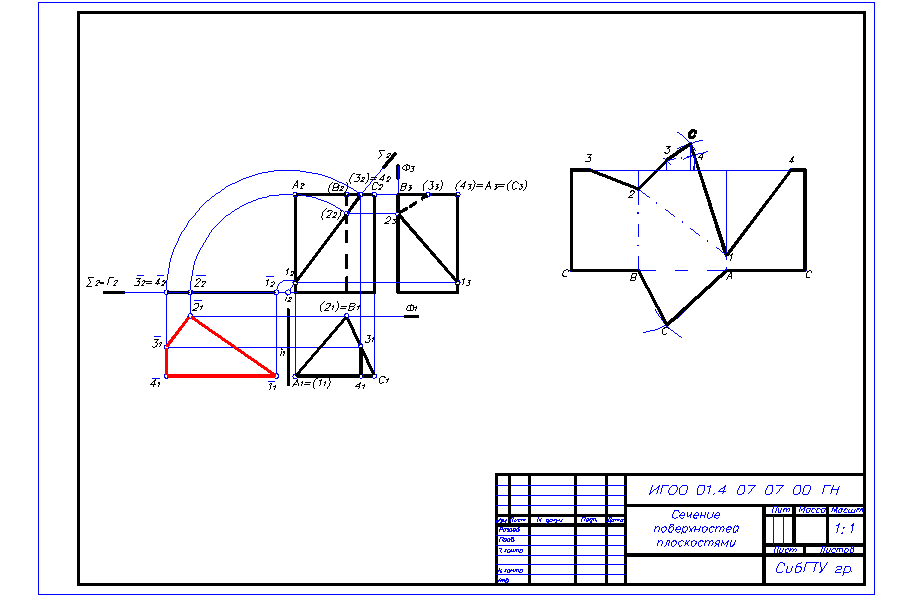

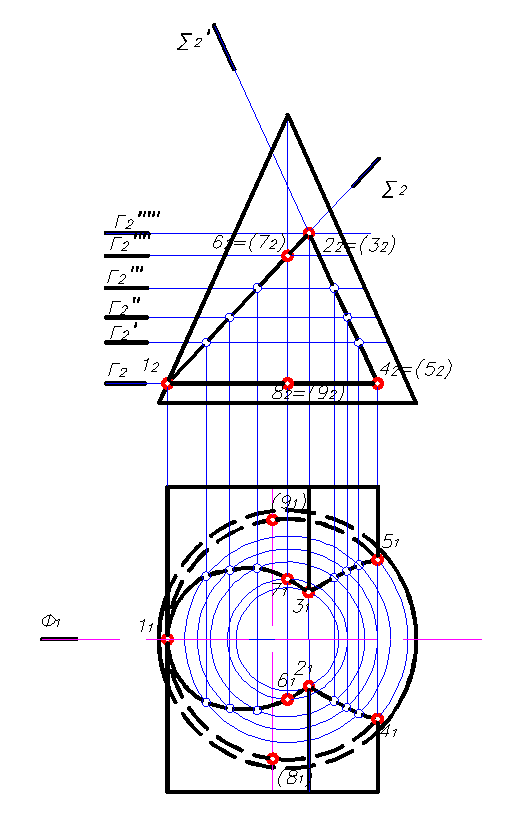
 Рисунок 26
Рисунок 26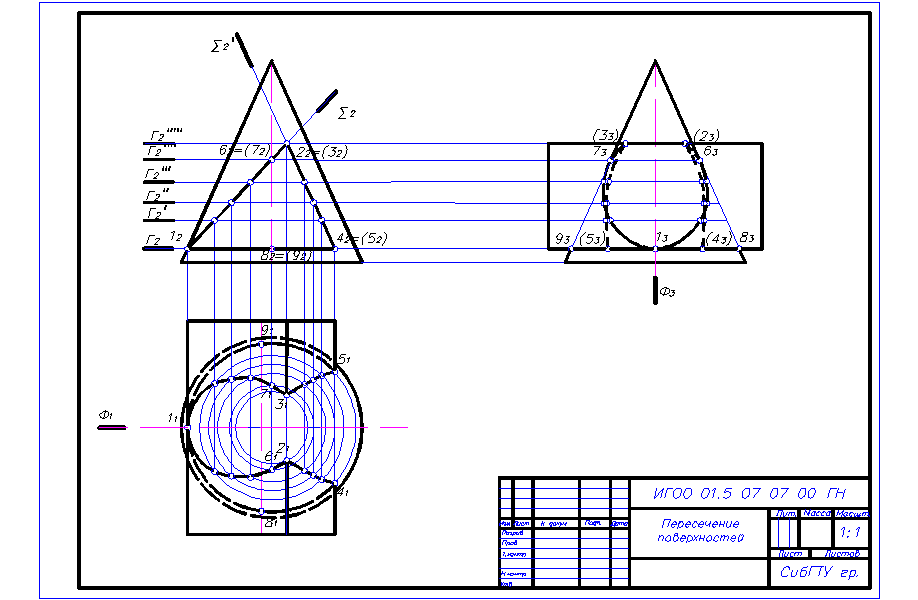
 , и пересекающую прямую АВ. Назвать эту прямую и записать ее натуральную величину.
, и пересекающую прямую АВ. Назвать эту прямую и записать ее натуральную величину.
 Разделить прямую АВ точкой К в отношении АК:КВ=2:5.
Разделить прямую АВ точкой К в отношении АК:КВ=2:5.