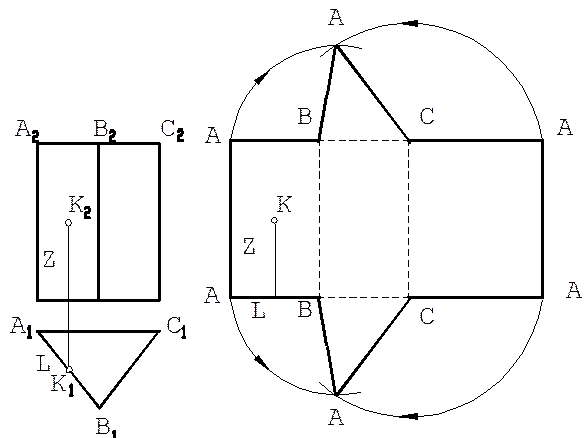|
|
Развертка прямого кругового цилиндра12 Рецензенты: доц. В.В.Силин (методический совет СибГТУ), проф. А.И.Лагерь (КГАЦМиЗ)
В сборнике приведены задания для контрольных работ по основным темам курса начертательной геометрии. Задания приведены в приложении. Каждое задание по теме представлено 30 вариантами индивидуальных заданий. В помощь студентам приведен краткий теоретический материал по каждой теме с примерами решения типовых задач. К каждому заданию приводится пример его оформления на чертежной бумаге. Сборник контрольных заданий рекомендуется для студентов технологических специальностей ВУЗов очной и заочной формы обучения, но может быть использован студентами других специальностей ВУЗов и техникумов независимо от формы обучения для самостоятельной работы. Для контроля и закрепления материала работа содержит контрольные вопросы по отдельным темам раздела.
ã И.И.Астапкович, Т.В.Борисова, Н.И.Лукьянчук,Е.Н.Первиненко. , 2004
ã ГОУ ВПО «Сибирский государственный технологический университет», 2004
Введение Данное учебное пособие предназначено для студентов технологических специальностей очной и заочной формы обучения. Сборник контрольных заданий рассчитан для курса «Начертательная геометрия» с объемом 32/16 лекционных часов и 32 часов практических занятий. В нем рассмотрены следующие темы курса: точка, прямая, плоскость, позиционные задачи, метрические задачи, поверхности. Цель учебного пособия состоит в оказании помощи студентам при выполнении контрольных заданий по начертательной геометрии. По указанным темам студенты очной формы обучения выполняют 5, а студенты заочной формы – 4 контрольных задания, каждое из которых содержит указания по их выполнению , примеры решения задач, контрольные вопросы по теоретическому курсу, варианты контрольных заданий и образцы их выполнения. Варианты заданий студентам очной формы обучения выдает преподаватель. Для студентов заочной формы обучения вариант соответствует сумме трех последних цифр шифра (№ зачетной книжки) или выдается преподавателем. При сдаче задания студент должен объяснить решение задач и ответить на теоретические вопросы по данной теме. Задания должны быть выполнены в сроки, предусмотренные учебным графиком выполнения работ, который выдается студенту в начале осеннего семестра. Задачи контрольных заданий решаются на практических занятиях и в процессе самостоятельной работы студентов. Тщательная и последовательная проработка этих заданий позволяет студентам приобрести достаточные практические навыки в решении аналогичных задач. Итогом курса «Начертательная геометрия» является экзамен. Для получения допуска на экзамен студент должен выполнить по своему варианту все задания, вошедшие в этот сборник, текущие контрольные мероприятия, решить задачи в рабочей тетради и выполнить зачетную работу. Использование методического пособия позволит сократить время, затрачиваемое преподавателем на индивидуальные консультации, и может быть рекомендовано для самостоятельной работы студентам ВУЗов других специальностей, учащимся техникумов, колледжей и лицеев.
Требования, предъявляемые к выполнению чертежей
1. Каждое задание контрольной работы выполняется на отдельном листе чертежной бумаги формата А3 ( 297х420).
2. Чертежи должны быть выполнены простым карандашом четко и аккуратно с помощью чертежных инструментов в соответствии с ГОСТами Единой системы конструкторской документации ГОСТ 2.301 3. Все элементы (точки, прямые, плоскости, линии) должны иметь буквенное обозначение. 4. На чертеже толщина и тип линий должны соответствовать ГОСТ 2.303 5. Основные построения сохраняются и проводятся тонкими сплошными линиями. 6. Точки, получаемые в результате построений, должны выполняться в виде незакрашенных окружностей диаметром 1,5 –2 мм. 7. Изображения проекций необходимо равномерно располагать на поле чертежа. 8. На чертеже должны быть проведены линии проекционной связи для основных построений. 9. В правом нижнем углу располагают основную надпись по ГОСТ 2.104
Заполнение основной надписи для студентов очной формы обучения
Шифр работы № в журнале № варианта
Графа 2 – Название работы Графа 3 – СибГТУ Гр.21-6
Заполнение основной надписи для студентов заочной формы обучения
Шифр(№зачетки) №листа № варианта
Графа 2 – Название работы Графа 3 – СибГТУ 2204-1к 10. Все надписи, буквенные и цифровые обозначения выполняются чертежным шрифтом по ГОСТ 2.304. Буквенные обозначения и цифры на поле чертежа выполняются шрифтом № 5. 11. Все чертежи сшиваются в альбом и оформляются титульным листом Задание 1 «Точка. Прямая» Целевое назначение
Закрепить знания студентов по решению задач на взаимное расположение в пространстве точек и прямых.
Содержание задания
Задание состоит из 7 задач. Задача 1. Построить три проекции отрезка прямой по заданным координатам 2-х точек. Задача 2. Построить 3 проекции точки по отношению к одной из заданных точек. Задача 3. Через заданную точку провести прямую, параллельную заданной. Задача 4. Через заданную точку провести прямую, параллельную одной из плоскостей проекций и пересекающую заданную прямую. Задача 5. Определить взаимное положение прямых и доказать это на чертеже. Задача 6. Разделить отрезок прямой в заданном отношении. Задача 7. Пересечь заданную прямую проецирующей прямой.
Указания к выполнению задания
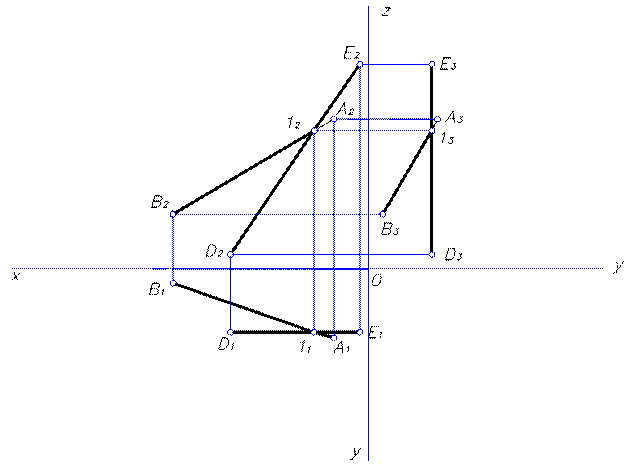
Задание выполняется в трех проекциях на чертежной бумаге формата А3 в масштабе 1:1 по номеру своего варианта заданий, данных на странице Перед выполнением задания необходимо изучить теоретический материал по заданной теме и ответить на контрольные вопросы. На рисунке 8 приведен пример выполнения задания. Примеры решения задач Задача 1 (Рисунок 1) Построить 3 проекции отрезка прямой АВ по заданным координатам точек: А (25,55,115) и В (150,5,45)
Алгоритм решения:
1. Проводим оси координат X, Y, Z. 2. По заданным координатам строим 3 проекции точек А (А и В (В 3. Одноименные проекции точек А и В соединяем и получаем фронтальную (А
Рисунок 1 Построить 3 проекции точки С, расположенной относительно точки А левее на 65 мм, дальше на 45 мм и ниже на 15 мм. Построить три проекции точки D, расположенной относительно точки В правее на 45 мм, ближе на 45 мм и ниже на 35 мм.
Алгоритм решения:
1. Проводим вертикальную линию связи левее на 65 мм от вертикальной линии связи для точки А ( А 2. От оси Х откладываем координаты Yc = Ya-45=55-45=10; Zc = Za-15=115-15=100 и находим проекции точки С ( C 3. Аналогичным образом строим проекции точки D (D
Рисунок 2
Задача 3 (Рисунок3) Через точку С провести прямую СF, параллельную прямой АВ
Алгоритм решения
1. Через горизонтальную проекцию точки С ( С 2. Через фронтальную проекцию точки С ( С 3. Через профильную проекцию точки С ( С параллельную прямой А 4. Координаты точки F выбираем произвольно.
Рисунок 3
Задача 4 (Рисунок4) Через точку D провести прямую DE, параллельную плоскости проекций П2 и пересекающую прямую АВ. Назвать эту прямую и записать ее натуральную величину.
Алгоритм решения:
1. Через горизонтальную проекцию точки D ( D 2. Находим фронтальную проекцию точки 1 (1 3. Соединяем фронтальную проекцию точки D (D 4. Ограничиваем прямую D1 точкой Е, которую выбираем произвольно. 5. Строим профильную проекцию прямой DE (D 6. Прямая DE называется фронтальной прямой уровня (фронталью). 7. Определяем натуральную величину прямой DE, для чего замеряем D
Рисунок 4
Задача 5 (Рисунок5) Определить взаимное положение прямых АВ и CD и доказать это на чертеже.
Алгоритм решения:
1. Взаимное положение прямых определяется с помощью конкурирующих точек. 2. В данном случае прямые АВ и CD называются пересекающимися, т.к. проекции их точки пересечения 2 ( 2
Рисунок 5
Задача 6 (Рисунок 6 ) Разделить прямую АВ точкой К в отношении АК : КВ = 5 : 2.
Алгоритм решения:
1. Из любого конца данного отрезка на любой проекции , например из А 2. На этой линии от точки А 3. Крайнюю точку В 4. Находим точку К 5. Из точки К 6. Находим фронтальную К
Рисунок 6
Задача 7 (Рисунок 7 ) Пересечь прямую АВ фронтально проецирующей прямой MN.
Алгоритм решения:
1. Произвольно проводим горизонтальную проекцию прямой MN (M 2. Находим фронтальную проекцию точки 3 (3 3. Строим профильную проекцию прямой M N (M 4. Определяем видимость прямой MN (M
Рисунок 7
Контрольные вопросы 1. Какой чертеж называется комплексным? 2. Как называются и обозначаются плоскости проекций? 3. Что такое линии связи на комплексном чертеже? 4. Как построить третью (профильную) проекцию точки? 5. В каком случае длина проекции отрезка равна длине самого отрезка? 6. В каком случае проекция прямой обращается в точку? 7. Какая прямая называется прямой общего положения? 8. Как по комплексному чертежу определить принадлежность точки прямой линии? 9. Какие прямые называются прямыми уровня? Как они обозначаются? 10. Что характерно для комплексного чертежа прямой уровня? 11. Какие прямые называются проецирующими? Как они обозначаются? 12. Какие точки называются конкурирующими? Как определить их видимость? 13. Как разделить отрезок в заданном отношении на комплексном чертеже? 14. Как могут располагаться в пространстве прямые по отношению друг к другу? 15. Какие прямые называются: а) параллельными? б) пересекающимися? в) скрещивающимися? 16. Как определить взаимное положение прямых по комплексному чертежу?
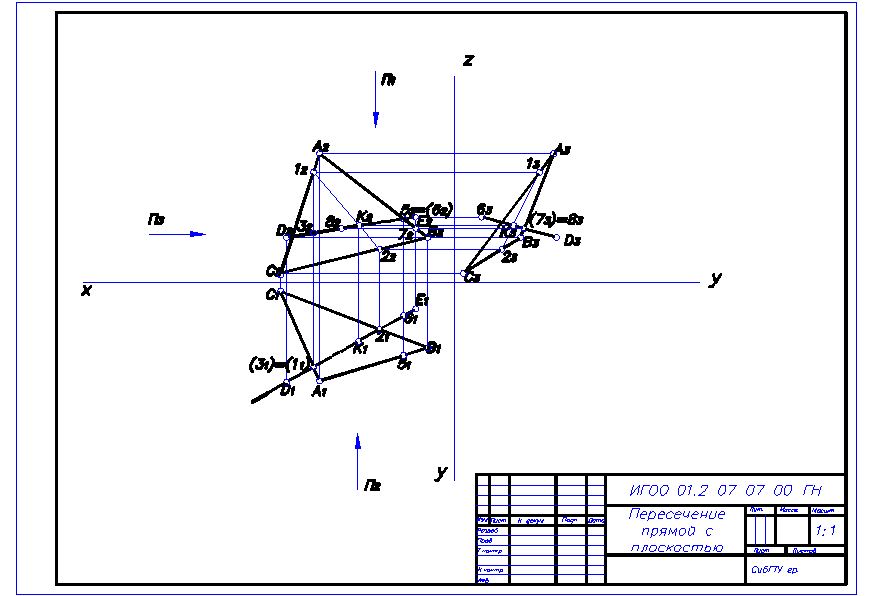
Рисунок 8 – Пример выполнения задания1 Задание 2 «Пересечение прямой с плоскостью» Целевое назначение
Закрепить знания студентов по решению задач на взаимное расположение в пространстве прямой и плоскости.
Содержание задания
Построить точку пересечения прямой с плоскостью, заданной координатами точек. Определить видимость прямой относительно плоскости на всех проекциях.
Указания к выполнению задания
1. Плоскость и прямая задаются координатами точек А,В,С и D,E. Координаты точек выбираются в соответствии с вариантом из таблицы 2.1 2. Задание выполняется в тех проекциях на чертежной бумаге формата А3 в масштабе 1:1 3. Плоскость треугольника при определении видимости считать непрозрачной. Перед выполнением задания необходимо изучить теоретический материал по заданной теме. На рисунке 9 приведен пример выполнения задания.
Пример решения задачи
Построить точку пересечения прямой DE с плоскостью треугольника АВС, заданных координатами точек. Определить видимость прямой DE относительно плоскости треугольника АВС.
Алгоритм решения:
1. Строим три проекции треугольника АВС и прямой DE по заданным координатам точек. 2. Прямую DE заключаем в проецирующую плоскость ( в данном случае во горизонтально проецирующую) Σ É DE ( в д.сл. Σ 1 É D1E1 ). 3. Находим линию пересечения плоскости Σ с плоскостью треугольника АВС. Σ Ç (АВС) = 1-2. 4. Искомую точку K пересечения прямой DE с плоскостью треугольника АВС находим как точку пересечения заданной прямой DE с найденной линией пересечения двух плоскостей d Ç (1-2) = К. 5. Видимость прямой DE относительно плоскости треугольника АВС определяем с помощью конкурирующих точек. На горизонтальной плоскости проекций П
Контрольные вопросы 1. Какой чертеж называется комплексным? 2. Как называются и обозначаются плоскости проекций? 3. Что такое линии связи на комплексном чертеже? 4. Как построить третью (профильную) проекцию точки? 5. В каком случае длина проекции отрезка равна длине самого отрезка? 6. В каком случае проекция прямой обращается в точку? 7. Какая прямая называется прямой общего положения? 8. Как по комплексному чертежу определить принадлежность точки прямой линии? 9. Какие прямые называются прямыми уровня? Как они обозначаются? 10. Что характерно для комплексного чертежа прямой уровня? 11. Какие прямые называются проецирующими? Как они обозначаются? 12. Какие точки называются конкурирующими? Как определить их видимость? 13. Как разделить отрезок в заданном отношении на комплексном чертеже? 14. Как могут располагаться в пространстве прямые по отношению к друг другу? 15. Какие прямые называются: а) параллельными? б) пересекающимися? в) скрещивающимися? 16. Как определить взаимное положение прямых по комплексному чертежу?
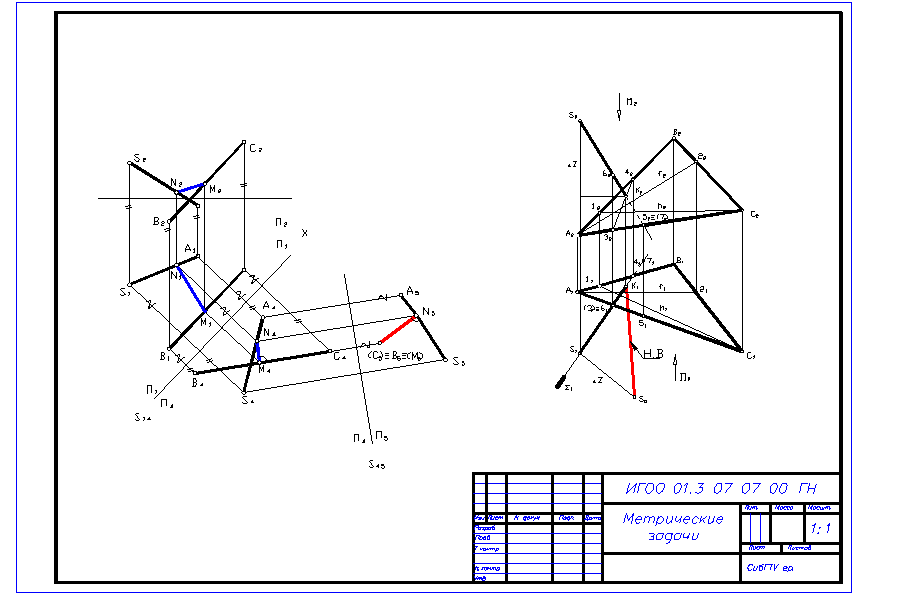
Рисунок 10. Пример выполнения задания 2 Задание 3 «Метрические задачи». Целевое назначение
Решение метрических задач, закрепление знаний студентов по следующему теоретическому материалу: 1. Перпендикулярность прямой и плоскости 2. Способ прямоугольного треугольника 3. Способы преобразования комплексного чертежа
Содержание задания
Задание состоит из 2-х задач.
Задача 1. Определить расстояние от точки S до плоскости треугольника АВС. Задача 2. Определить кратчайшее расстояние между отрезками прямых SA и ВС способом перемены плоскостей проекции. Указания к выполнению задания 1. Графическая работа выполняется на формате А3. На поле листа вычерчиваются две отдельные задачи. 2. Для каждой задачи вычерчиваются только те элементы, которые необходимы для ее решения. 3. Задачи решаются в 2-х проекциях. Перед выполнением задания необходимо изучить теоретический материал по заданной теме и ответить на контрольные вопросы. Варианты задач приведены в таблице 3.1 На рисунке 13 приведен пример выполнения задания.
Задача 1 (Рисунок 11) Определить расстояние от точки S до плоскости треугольника АВС.
Алгоритм решения:
1. Строим проекции точки S и треугольника АВС. 2. Из точки S опускаем перпендикуляр на плоскость треугольника АВС. (Горизонтальная проекция перпендикуляра перпендикулярна горизонтальной проекции горизонтали, а фронтальная проекция перпендикуляра перпендикулярна фронтальной проекции фронтали). 3. Определяем точку пересечения перпендикуляра с плоскостью треугольника АВС. (Для этого заключаем одну из проекций перпендикуляра в проецирующую плоскость S. Находим линию пересечения плоскости S с плоскостью треугольника АВС. В пересечении этой линии с перпендикуляром находим точку К пересечения перпендикуляра с плоскостью треугольника АВС). 4. Методом прямоугольного треугольника находим натуральную величину перпендикуляра SK. 5. С помощью конкурирующих точек определяем видимость перпендикуляра относительно плоскости треугольника АВС.
Рисунок 11 Задача 2 (Рисунок 11) Определить кратчайшее расстояние между отрезками прямых SA и ВС способом перемены плоскостей проекции.
Алгоритм решения:
1. Строим проекции отрезков прямых SA и ВС. 2. Последовательным введением двух дополнительных плоскостей проекций одну из скрещивающихся прямых преобразуем в проецирующую прямую (спроецируем в точку). В нашем примере в проецирующую прямую преобразована прямая ВС. При первой замене ось S14 проведена параллельно проекции В1С1, а при второй замене ось S45 проведена перпендикулярно проекции В4 С4. 3. Расстояние между скрещивающимися прямыми определяется перпендикуляром, опущенным из проекции проецирующей прямой (точки) на проекцию второй прямой.
Рисунок 12 Контрольные вопросы
1. Теорема о проецировании прямого угла. 2. Сформулировать признак перпендикулярности прямой и плоскости. 3. Как построить проекции прямой, перпендикулярной к заданной прямой общего положения? 4. В чем состоит признак перпендикулярности двух плоскостей? 5. Как определить угол наклона прямой к заданной плоскости? 6. Для чего нужны методы преобразования комплексного чертежа? 7. Сущность метода замены плоскостей проекций. 8. Сущность метода вращения вокруг проецирующей прямой. 9. Сущность метода вращения вокруг прямой уровня. 10. Плоско параллельное перемещение.
Задание 4 «Сечение поверхностей плоскостями» Целевое назначение Закрепить знания студентов по следующему теоретическому материалу: 1. Нахождение точек на поверхностях геометрических тел 2. Пересечение поверхностей c плоскостями частного положения. 3. Нахождение натуральной величины фигуры, полученной в пересечении поверхности c плоскостью частного положения. 4. Построение разверток поверхностей.
Содержание задания Задание состоит из 4-х задач:
Задача 1 1. Построить три проекции геометрического тела и линию пересечения его поверхности с плоскостью S. 2. Найти натуральную величину фигуры полученной в пересечении. 3. Построить полную развертку усеченной части геометрического тела. 4. Из чертежной бумаги выполнить модель усеченной части геометрического тела.
Задача 2 Построить три проекции геометрического тела с вырезом или сквозным отверстием.
Задача 3 и 4 Построить три проекции геометрических тел и найти недостающие проекции заданных точек, лежащих на поверхности этих геометрических тел.
Указания к выполнению задания Задание выполняется на 2-х форматах А3 чертежной бумаги в масштабе 1:1 по номеру своего варианта заданий, данных на странице На первом листе располагается решение 1-й задачи. На втором листе располагаются задачи 2, 3 и 4. Размеры на чертеже не проставлять. При вычерчивании проекций геометрическое тело считать непрозрачным и отсеченную часть не отбрасывать. Натуральную величину фигуры, полученной в пересечении тела с плоскостью найти любым способом. Перед выполнением задания необходимо изучить теоретический материал по заданной теме и ответить на контрольные вопросы. На рисунках 23 и 24 приведены примеры выполнения задания. Построение разверток геометрических тел Разверткой геометрической поверхности называется фигура, полученная путем совмещения ее поверхности с плоскостью. Развертывание поверхности многогранников состоит в последовательном вычерчивании в плоскости чертежа его граней в натуральную величину в том порядке, в каком эти грани расположены в пространстве. Последовательность в расположении граней на развертке может быть различна. Из этого следует, что необходимо построить развертку с минимальной общей длиной швов (выполняемых при помощи электросварки, клея и т.п.) Для построения развертки мысленно “разрезаем” многогранную поверхность по одному из ребер (призма, пирамида), а поверхность вращения по образующей (цилиндр, конус). При этом необходимо учесть, что развертка не может состоять из нескольких отдельных, не связанных между собой участков, а у многогранных поверхностей не должно быть соединения граней в одной точке. Если секущая плоскость пересекает основание геометричекого тела, то построение развертки рекомендуется начинать с ребра или очерковой образующей, не участвующей в пересечении с плоскостью.
Развертка прямой призмы Развертывание поверхности прямых призм, у которых все углы боковых граней прямые, выполняется непосредственно, без преобразования проекций, т.к. ребра прямой призмы являются горизонтально проецирующими прямыми, а плоскости оснований – горизонтальными плоскостями уровня. Так, для того, чтобы построить развертку боковой поверхности треугольной, прямой правильной призмы (рисунок 14, проводим прямую и, отложив на ней три отрезка AB, BC и CA, из которых каждый равен стороне основания призмы, строим прямоугольник с высотой, равной высоте призмы. Полную развертку призмы получим, если к верхней и нижней сторонам какой-нибудь развернутой грани пристроим верхнее и нижнее основание призмы. Точку К, расположенную на грани АВ находим на развертке грани АВ на высоте z и на расстоянии l от ребра А.
Рисунок 14
Развертка пирамиды Построение развертки боковой поверхности пирамиды сводится к последовательному построению ряда треугольников (по трем их сторонам), каждый из которых равен натуральной величине соответствующей боковой грани пирамиды. Чтобы построить развертку треугольной пирамиды (рисунок 15, необходимо определить натуральные величины ребер пирамиды любым способом. Если ребер много, то удобно воспользоваться способом прямоугольного треугольника. При этом нужно вынести построения всех треугольников в сторону от чертежа данной фигуры. Натуральные величины ребер можно найти и методом вращения вокруг горизонтально проецирующей оси i, проходящей через вершину S. На рисунке 15 показаны оба способа нахождения натуральных величин ребер пирамиды. После того, как определим длины ребер SA, SB, SC, приступаем к построению развертки. Для этого через произвольно выбранную точку S проводим прямую l, на которой откладываем натуральную величину ребра AS. Далее строим вершину B треугольника ABS методом засечек, затем вершину С треугольника BCS и вершину А треугольника CAS. После этого достраиваем к полученной развертке боковой поверхности основание пирамиды АВС, взятое с плоскости П1, на которую оно проецируется в натуральную величину, т.к. является горизонтальной плоскостью уровня. На рисунке 15 показано нахождение на развертке точки К, расположенной на грани ABS.
Рисунок 15
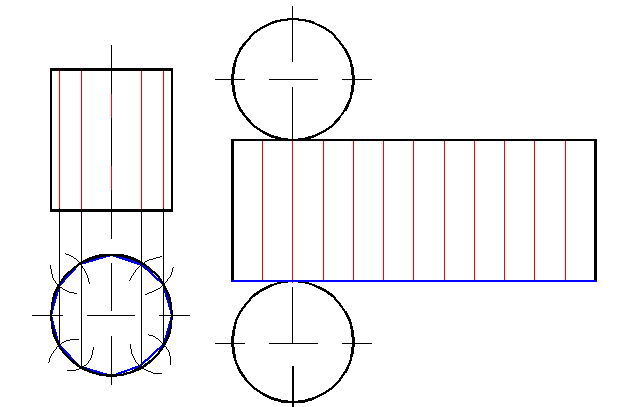
Развертка прямого кругового цилиндра Полная развертка прямого кругового цилиндра представляет собой прямоугольник, высота которого равна высоте цилиндра, а основание – длине окружности основания цилиндра и пристроенные к нему два круга-основания. Для получения приближенной развертки цилиндрической поверхности заменяем последнюю на вписанную в нее 12-ти угольную правильную призму (рисунок 16).
Рисунок 16 
12 Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
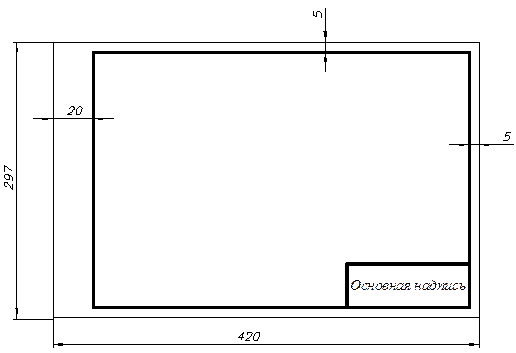


 Графа 1 ИГ00 01.1 07 12 00 ГН
Графа 1 ИГ00 01.1 07 12 00 ГН


 Графа 1 060215 01 07 00 ГН
Графа 1 060215 01 07 00 ГН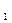 , А
, А 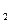 , А
, А  )
)




 последней отложенной части соединяем с В
последней отложенной части соединяем с В 



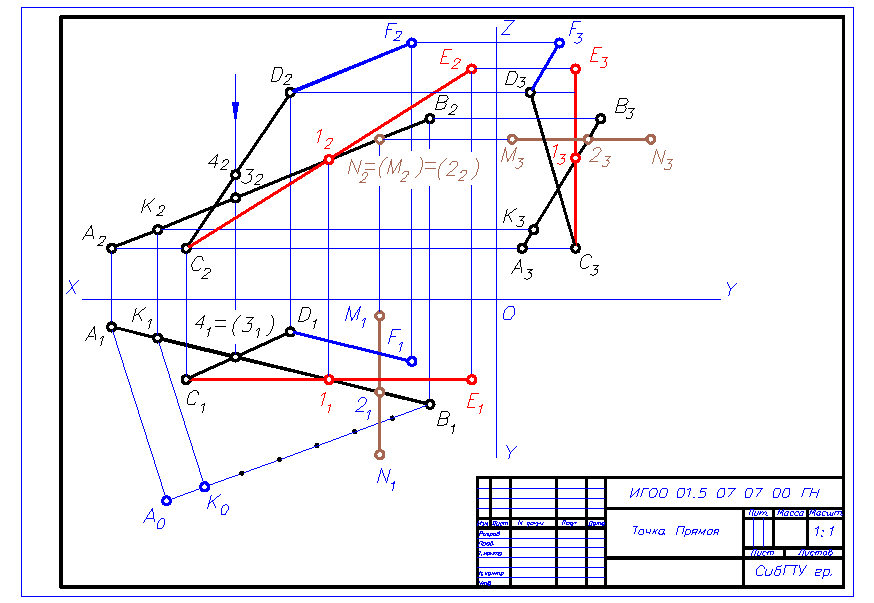
 Рисунок 9
Рисунок 9