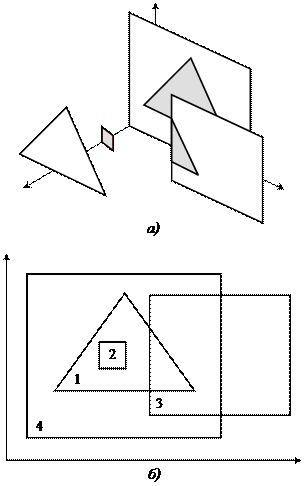Алгоритм Вейлера – Азертона

В этом алгоритме сделана попытка минимизации количества шагов в алгоритме типа Варнока путем разбиения окна вдоль границ многоугольника. Основа этого алгоритма - алгоритм Вейлера – Азертона для отсечения многоугольников [1]. Алгоритм работает в пространстве объекта и его легко использовать как для удаления невидимых линий, так и невидимых поверхностей. Алгоритм состоит из четырех шагов:

- предварительная сортировка по глубине;

- отсечение по границе ближайшего к наблюдателю многоугольника;

- удаление многоугольников, экранированных многоугольником, ближайшим к точке наблюдения;

- если требуется, то рекурсивное подразбиение и окончательная сортировка.

Предварительная сортировка по глубине необходима для формирования списка приблизительных приоритетов. Если точка наблюдения расположена в бесконечности на положительной полуоси z, то ближайшим многоугольником будет считаться многоугольник с максимальным значением z. В качестве отсекающего многоугольника используется копия первого многоугольника из предварительного списка по глубине. Отсекаться будут оставшиеся в этом списке многоугольники, в том числе и первый. С помощью алгоритма отсечения многоугольников Вейлера – Азертона все многоугольники отсекаются по границам отсекающего многоугольника. Вводится два списка: внутренний и внешний. Та часть отсекаемого многоугольника, которая оказывается внутри отсекающего, попадает во внутренний список, оставшаяся часть – во внешний список. Пример сцены и ее проекции на плоскость XY приведены на рис. 5.1, a и 5.1, б соответственно, а на рис. 5.2 – внутренний и внешний списки.

Теперь сравниваются глубины вершин многоугольников из внутреннего списка с глубиной отсекающего Zmin. Если глубина ни одной из этих вершин не будет больше Zmin, то все многоугольники из внутреннего списка экранируются отсекающим (кроме него самого) и этот многоугольник изображается. Внутренний список очищается, а работа продолжается с внешним списком.

Если глубина z какого – либо многоугольника из внутреннего списка окажется больше Zmin (рис. 5.3), то такой многоугольник может частично экранировать отсекающий многоугольник. В этом случае результат предварительной сортировки по глубине ошибочен и алгоритм рекурсивно использует новый отсекающий многоугольник. Отсечению подлежат многоугольники из внутреннего списка, причем отсекающий многоугольник является копией исходного, а не его остатком во внешнем списке.

Рис. 5.1. Пример сцены для алгоритма Вейлера - Азертона

Рис. 5.2. Внутренний и внешний списки многоугольников

Рис.5.3. Условие возникновения ошибочного
результата в предварительной сортировке по z

При циклическом перекрытии многоугольников (рис. 5.4) в рекурсивном подразбиении необходимости нет. Все, что было экранировано циклическим многоугольником, уже было удалено на предыдущем шаге отсечения. Необходимо лишь произвести отсечение исходного многоугольника по границам циклического многоугольника и изобразить результат.

Рис. 5.4. Циклически перекрывающиеся многоугольники

Для исключения ненужного рекурсивного разбиения используется список многоугольников, которые уже использовались в качестве отсекающих многоугольников.

6. Алгоритмы, использующие список
приоритетов

При реализации алгоритмов удаления невидимых линий и поверхностей основная сортировка производится по глубине, то есть по расстоянию от наблюдателя. Таким образом, устанавливаются приоритеты, и цель сортировки состоит в получении окончательного списка элементов сцены. Если такой список окончателен, то никакие два элемента не будут взаимно перекрывать друг друга. В этом случае можно записать все элементы в буфер кадра поочередно, начиная с элемента, наиболее удаленного от наблюдателя. При этом более близкие элементы будут затирать информацию о более далеких элементах. Эффекты прозрачности можно учесть путем коррекции содержимого буфера кадра с учетом атрибутов прозрачности элементов.

Для сцены, показанной на рис. 6.1, a, окончательный список приоритетов можно получить непосредственно. Но для сцены, показанной на рис. 6.1, б, окончательный список приоритетов по глубине невозможно получить простой сортировкой по оси z.

Рис. 6.1. Установление приоритетов для многоугольников

Если отрезки P и Q упорядочены по минимальному значению z – Zmin, то отрезок P в списке будет стоять перед отрезком Q и получится, что отрезок Q частично перекрывает отрезок P, хотя на самом деле это не так. В этом случае необходимо поменять местами отрезки P и Q в списке приоритетов.

Другие трудности возникают при циклическом перекрытии многоугольников (рис. 6.2). На рис. 6.2, a многоугольник P находится впереди многоугольника Q, который лежит впереди многоугольника R, который в свою очередь находится впереди многоугольника P. На рис. 6.2, б многоугольник P экранирует многоугольник Q, а многоугольник Q экранирует многоугольник P. В обоих случаях окончательный список сразу определить невозможно. Решение заключается в циклическом разрезании многоугольников по линиям, образованным пересечениями их плоскостей до тех пор, пока не будет получен окончательный список приоритетов. На рис. 6.2 эти линии показаны пунктиром.

Рис. 6.2. Циклически перекрывающиеся многоугольники

Ньюэл М., Ньюэл Р. и Санча предложили специальный список сортировки. В этом алгоритме не накладывается никаких ограничений на сложность сцены и тип многоугольников.

7. Алгоритм Ньюэла – Ньюэла – Санча
для случая многоугольников

Сформировать предварительный список по глубине, используя в качестве ключа сортировки значение Zmin для каждого многоугольника. Обозначим первый в списке многоугольник (с минимальным значением Zmin) как многоугольник P, а следующий в списке многоугольник как многоугольник Q.

Для каждого многоугольника P надо проверить его отношение с многоугольником Q:

- если ближайшая вершина P (PZmax) будет дальше от точки наблюдения, чем самая удаленная вершина Q (QZmin), то есть QZmin ≥ PZmax, то никакая часть многоугольника P не может экранировать многоугольник Q. Занести P в буфер кадра;

- если QZmin < PZmax, то P потенциально экранирует не только Q, но любой многоугольник типа Q из списка, для которого QZmin < PZmax. Тем самым образуется множество [Q]. Однако многоугольник P может фактически и не экранировать ни один из этих многоугольников. Если последнее верно, то P можно заносить в буфер кадра (с учетом эффектов прозрачности). Для определения факта перекрытия используется серия тестов. Эти тесты можно сформулировать в виде вопросов, и если ответ на любой вопрос будет положительным, то многоугольник P не может экранировать множество многоугольников [Q]. Поэтому многоугольник P заносится сразу в буфер кадра. Тесты определяются следующим образом:

- верно ли, что прямоугольные оболочки P и Q не перекрываются по x?

- верно ли, что прямоугольные оболочки P и Q не перекрываются по y?

- верно ли, что многоугольник P целиком лежит по ту сторону плоскости, несущей Q, которая расположена дальше от точки наблюдения (рис. 7.1, a)?

- верно ли, что многоугольник Q целиком лежит по ту сторону плоскости, несущей P, которая расположена ближе к точке наблюдения (рис. 7.1, б)?

- верно ли, что проекции P и Q не перекрываются?.

Каждый из этих тестов применяется к каждому элементу [Q]. Если ни один из них не дает положительного ответа и не заносит P в буфер кадра, то P может закрывать Q.

Рис. 7.1. Тесты для перекрывающиеся многоугольников

Поменять P и Q местами.

Повторить тесты с новым списком.

Если сделана попытка вновь переставить Q, то обнаружена ситуация циклического экранирования (рис. 6.2). Тогда необходимо разрезать многоугольник P плоскостью, несущей многоугольник Q. Исходный многоугольник P удаляется из списка, а его части заносятся в список. Затем тесты повторяются для нового списка.

литература

1. Роджерс Д. Алгоритмические основы машинной графики: Пер. с англ. – М.: Мир, 1989. – 504 с., ил.

2. Роджерс Д., Адамс Дж. Математические основы машинной графики: Пер. с англ. – М.: Машиностроение, 1980. – 240 с., ил.

3. Фоли Дж., вэн Дэм А. Основы интерактивной машинной графики: В 2-х книгах. Пер. с англ. – M.: Мир, 1985.

4. Вельтмандер П.В. Алгоритмы компьютерной графики: http://ermak.cs.nstu.ru/kg_rivs

5. Демин А.Ю., Кудинов А.В. Компьютерная графика: Учеб. пособие. – Томск: Изд. ТПУ, 2004, 138с., ил.

6. Donald Hearn, M. Pauline Baker. Computer graphics: - Prentice Hall, Inc, 1994. – 652 c., ил.

ОГЛАВЛЕНИЕ

Введение. 3

1. Алгоритм плавающего горизонта. 5

2. Алгоритм Робертса. 13

3. Алгоритм Варнока. 14

4. Алгоритмы, использующие z – буфер. 25

5. Алгоритм Вейлера – Азертона. 28

6. Алгоритмы, использующие список приоритетов. 32

7. Алгоритм Ньюэла – Ньюэла – Санча для случая многоугольников 34

Литература. 36

Не нашли, что искали? Воспользуйтесь поиском по сайту: