|
|
Алгоритм плавающего горизонта12 А.И. ДРУЖИНИН АЛГОРИТМЫ КОМПЬЮТЕРНОЙ Часть 2
Удаление невидимых линий и поверхностей.
Утверждено Редакционно-издательским советом университета
НОВОСИБИРСК
Рецензенты: канд. техн. наук, ст. преп. Е.Л. Веретельникова канд. педагог. наук, доцент В.В. Вихман
Работа подготовлена на кафедре
Дружинин А.И. Алгоритмы компьютерной графики: Учеб. пособие. –
В учебном пособии рассмотрены основополагающие алгоритмы, используемые в компьютерной графике для удаления невидимых линий и поверхностей. Пособие адресовано студентам, изучающим курс "Компьютерная и инженерная графика", а также может быть полезно разработчикам программного обеспечения. Автор выражает благодарность выпускнику кафедры вычислительной техники Войнову В.Н. за возможность использования в данном пособии материалов его дипломного проекта.
Новосибирский государственный технический университет, 2007 г. Введение Алгоритмы удаления невидимых линий и поверхностей служат для определения линий, ребер, поверхностей или объемов, которые видимы или не видимы для наблюдателя, находящегося в заданной точке пространства. Это одна из наиболее сложных задач в компьютерной графике[1]. Сложность задачи можно проиллюстрировать следующим примером (рис. В.1). На рис В.1, а приведен каркасный чертеж четырехгранной пирамиды [6]. Его можно интерпретировать двояко: как вид пирамиды спереди, (рис В.1, б) или снизу (рис. В.1, в).
Рис. В.1. Необходимость удаления невидимых линий Существует множество способов решения задачи удаления невидимых линий и поверхностей. Одни из них ориентированы на специальные приложения (то есть, улучшаются одни параметры и ухудшаются другие – такие как скорость построения, детализация прорисовки и т.д.). Другие, ориентированные на выполнение «общих» задач, пытаются оптимизировать все параметры наилучшим образом (по мнению авторов алгоритма). Несмотря на множественность решений, все алгоритмы включают в себя сортировку. И главная сортировка – сортировка по геометрическому расстоянию от тела, поверхности, ребра, точки до точки наблюдения (наблюдателя). Обычно, это сортировка по оси Z. Основной смысл этой сортировки – чем дальше объект расположен от точки наблюдения, тем больше вероятность, что он будет полностью или частично заслонен одним из объектов, более близких к наблюдателю. После определения приоритетов по глубине (сортировка по расстоянию до точки наблюдения) остается провести сортировку по горизонтали и вертикали, чтобы выяснить, будет ли рассматриваемый объект действительно заслонен объектом, расположенным ближе к точке наблюдения. Таким образом, эффективность алгоритмов зависит от эффективности алгоритмов сортировки. Алгоритмы удаления невидимых линий и поверхностей можно классифицировать по способу выбора системы координат или пространства, в котором они работают. Выделяется два класса алгоритмов удаления невидимых линий и поверхностей: - алгоритмы, работающие в объектном пространстве; - алгоритмы, работающие в пространстве изображения. Алгоритмы, работающие в объектном пространстве, имеют дело с физической системой координат, в которой описаны эти объекты. При этом получаются точные результаты, ограниченные лишь точностью вычислений. Полученные изображения можно изменять (увеличивать, уменьшать, «закручивать» и т.д.) без изменения точности изображения. То есть, алгоритмы, работающие в объектном пространстве, необходимы там, где необходима высокая точность. Алгоритмы, работающие в пространстве изображения, имеют дело с системой координат того экрана, на котором они визуализируются. При этом точность вычислений ограничена разрешающей способностью экрана. При изменении объекта полученная сцена может не соответствовать исходной сцене. Обычно, алгоритмы работают попеременно в обоих пространствах. В настоящее время, в связи с тем, что наиболее используемыми являются растровые устройства, наибольший интерес представляют алгоритмы, работающие в пространстве изображения. Однако, математические методы, используемые в алгоритмах, работающих в объектном пространстве, являются более простыми, мощными и эффективными и используются в современных системах компьютерной графики. Алгоритм плавающего горизонта Алгоритм плавающего горизонта используется для удаления невидимых линий и поверхностей трехмерного представления функций, описывающих поверхность в виде: F (x,y,z) = 0 Такие задачи возникают во многих приложениях математики, физики, техники и т.д. На основе этого алгоритма получаются так называемые каркасные или скелетные изображения трехмерного объекта на плоском (двумерном) экране. Впоследствии, эти изображения «обрастают плотью» при помощи алгоритмов закраски. Пример изображения при пересечении одной последовательностью секущих плоскостей показан на рис.1.1, двумя последовательностями секущих плоскостей (перекрестная штриховка) показан на рис.1.2.
Рис. 1.1. Результат работы алгоритма плавающего Данный метод заключается к сведению двумерной задачи к трехмерной путем пересечения исходной поверхности последовательностью параллельных секущих плоскостей, имеющих постоянные значения координат X, Y или Z. Пример для Z = const показан на рис. 1.3.
Рис. 1.2. Результат работы алгоритма плавающего При этом, функция F(x,y,z) = 0 сводится к последовательности кривых, лежащих в каждой из параллельных секущих плоскостей. В случае Z = const на каждой из заданных параллельных секущих плоскостей это, функция: y = f(x,z) Поверхность, в данном случае, складывается из последовательности кривых, лежащих в каждой из этих плоскостей (рис. 1.4) Если спроецировать полученные кривые на плоскость XY (Z = 0), (рис. 1.5), то мы получим «основу» для алгоритма плавающего горизонта. Алгоритм сначала упорядочивает плоскости Z = const по возрастанию расстояния до них от точки наблюдения (предполагается, что она находится в бесконечности на оси Z). Затем для каждой плоскости, начиная с ближайшей к точке наблюдения, строится кривая, лежащая на ней, то есть для каждого X определяется Y. И алгоритм удаления невидимых линий и поверхностей заключается в следующем: - если на текущей плоскости при некотором заданном значении X соответствующее значение Y больше, чем для всех предыдущих кривых при данном значении X, то текущая кривая видима в этой точке, иначе – невидима.
Рис. 1.3. Секущие плоскости с постоянной координатой
Рис. 1.4. Кривые в секущих плоскостях с
Рис. 1.5. Проекция кривых на плоскость XY (z = 0) Для реализации алгоритма предлагается следующее: для хранения максимальных значений Y при каждом значении X используется массив, длина которого равна разрешению по оси X в пространстве изображения. Значения, хранящиеся в этом массиве, представляют собой текущее значение «горизонта». Поэтому, по мере рисования каждой очередной кривой этот горизонт «всплывает» (отсюда и название алгоритма). Алгоритм работает, пока какая-нибудь из кривых не окажется ниже самой первой (рис. 1.6). Следовательно, «включаем» и нижний горизонт, который опускается вниз по ходу работы алгоритма (тонет). Нижний горизонт реализуется при помощи второго массива, который содержит минимальное значение Y для каждого значения X.
Рис. 1.6. Обработка нижней стороны проекции Алгоритм прост и эффективен, однако, следует учесть и некоторые нестандартные ситуации. Ранее предполагалось, что значение функции Y известно для всех значений X. Но, в некоторых приложениях, известны только несколько точек, а остальная функция «достраивается» c помощью линейной интерполяции. В данном случае, при изменении видимости не всегда возможно поддерживать правильные значения верхнего и нижнего горизонтов. На рис. 1.7, a кривая a – является «текущей» линией, а кривая b – «последующей». Причем, значения Y известны только в точках X = A, B, C, D и E, остальные значения получены с помощью линейной интерполяции. Если операция по заполнению массивов горизонтов проводится после проверки видимости, то на участке от B до C кривая b объявляется невидимой, так как точка с координатой X = C невидима, а от D до E – видимой, так как точка с координатой X= E видима (рис. 1.7, б). Следовательно, необходимо решать задачу поиска точек пересечения сегментов «текущей» и «последующей» кривых. Один из методов – добавлять единицу к значению X (то есть, брать следующую точку растра) и проверять видимость, другой - использовать метод деления пополам для нахождения точек пересечения. Точки пересечения необходимо искать и в случае, если функция содержит очень острые участки (рис. 1.8) и видимость «последующей» кривой не изменяется. Еще один нежелательный эффект – эффект зазубренного ребра, когда кривая, лежащая в одной из более удаленных от точки наблюдения плоскостей, появляется слева или справа из-под множества кривых, лежащих в плоскостях, которые ближе к указанной точке наблюдения. Пусть ранее были построены кривые a и b (рис. 1.9, а). После обработки кривых верхний горизонт от точки x = A до точки x = C будет принадлежать кривой b и, далее, до точки x = D – кривой a. Нижний горизонт от точки x = A до точки x = B будет принадлежать кривой b и, далее, до точки x = D – кривой a. Необходимо определить видимость новой кривой c (рис. 1.9, б). В данном случае, она объявляется видимой до точки B (ниже нижнего горизонта), от точки E до точки F и от точки C до точки G (выше верхнего горизонта). Однако, на самом деле участки от H до B и от C до I невидимы (рис. 1.9, в). Следовательно, необходимо включить в массивы горизонтов значения Y для боковых ребер. Причем эти ребра можно не изображать (рис. 1.10а), а можно и изобразить (рис. 1.10, б).
Рис. 1.7. Эффект пересекающихся кривых при
Рис. 1.8. Эффект «острых участков»
Рис. 1.9. Эффект зазубренного ребра
В приведенном выше алгоритме функция y = f(x,z) рассматривалась при z = const. Но, часто, удобнее вычерчивать кривые, полагая постоянными как z, так и x. При этом возникает, так называемый, эффект перекрестной штриховки (рис. 1.2). При этом это не наложение для двух плоскостей, а более сложный алгоритм. Более подробно о нем можно узнать в [1, 6].
Рис. 1.10. Устранение эффекта зазубренного ребра
Алгоритм Робертса Алгоритм Робертса представляет собой первое известное решение задачи об удалении невидимых линий и поверхностей. Этот алгоритм работает в пространстве объекта. Алгоритм, прежде всего, удаляет из каждого тела те ребра или грани, которые экранируются самим телом. Затем каждое из видимых ребер каждого тела сравнивается с каждым из оставшихся тел для определения того, какая его часть экранируется этими телами. Вычислительная трудоемкость алгоритма Робертса растет теоретически как квадрат числа объектов. В настоящее время в связи с широким применением растровых устройств наиболее распространены алгоритмы, работающие в пространстве изображения, имеющие более низкую вычислительную трудоемкость, равную произведению числа объектов на разрешающую способность экрана визуализации. Это привело к снижению интереса к алгоритму Робертса. Но математические методы, используемые в алгоритме, применяются в большинстве современных приложений компьютерной графики. Наконец, более поздние реализации алгоритма, использующие предварительную сортировку по расстоянию от точки наблюдения, в сочетании с простыми габаритными (или минимаксными) тестами демонстрируют почти линейную зависимость вычислительной трудоемкости от числа объектов. Более подробно данный алгоритм будет рассмотрен в третьей части учебного пособия, так как для его понимания необходимо предварительно рассмотреть некоторые основы компьютерной геометрии. Алгоритм Варнока Алгоритм основывается на гипотезе о способе обработки информации, содержащейся в сцене, глазом и мозгом человека [1]. Эта гипотеза заключается в том, что тратится очень мало времени и усилий на обработку тех областей, которые содержат мало информации. Большая часть времени и труда затрачивается на области с высоким информационным содержанием. «Классический» пример: поверхность стола, на котором нет ничего, кроме вазы с предметами (рис. 3.1). Для восприятия цвета, фактуры и других характеристик всей поверхности стола много времени не нужно. Все внимание сосредотачивается на вазе. В каком месте стола она расположена, из какого материала сделана, какие предметы, какого они цвета и так далее?
Рис. 3.1. Алгоритм Варнока В каждом случае, по мере сужения интересов, возрастает уровень требуемой детализации. Если на определенном уровне детализации на конкретный вопрос ответить нельзя, то он откладывается на время для последующего рассмотрения. Алгоритм Варнока работает в пространстве изображения. В этом пространстве рассматривается окно и решается вопрос о том, пусто ли оно, или его содержимое достаточно просто для визуализации. Если это так, то окно изображается. Если нет, то оно разбивается на части до тех пор, пока содержимое подокна не станет достаточно простым для визуализации или пока размер подокна не достигнет предела разрешения экрана. В последнем случае информация, содержащаяся в окне, усредняется, и оно изображается.
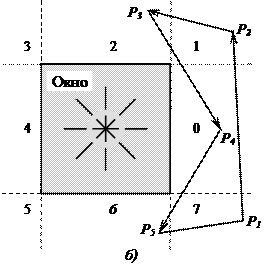
В оригинальной версии алгоритма окно, содержимое которого слишком сложно изображать, разбивается на 4 подокна. Окно, в котором что-то есть, разбивается далее до тех пор, пока не будет достигнут предел разрешения экрана. Для устранения лестничного эффекта возможно дальнейшее разбиение. В качестве примера рассмотрим сцену, изображенную на Окно слишком сложно для визуализации, следовательно, разбиваем его на 4 части (рис. 3.2, б) и рассматриваем левое нижнее подокно первого разбиения. Опять слишком сложно – разбиваем на 4 части (рис. 3.2, в). Левое нижнее подокно после второго разбиения пусто – изображаем его цветом фона. Возвращаемся к правому нижнему подокну второго разбиения – снова сложно, разбиваем его на 4 части (рис. 3.2, г) и так далее. В конце концов, при N-ном разбиении достигаем размеров пиксела (рис. 3.2, д). Теперь необходимо «вспомнить» какой алгоритм мы применяем – удаления невидимых линий или поверхностей. В случае удаления невидимых линий – окрашиваем левое и правое нижние и верхнее левое подокна в цвет многоугольника, а правое верхнее – в цвет фона. Затем возвращаемся к предыдущим подокнам и так далее. Результат показан на рис. 3.3. В случае удаления невидимых поверхностей – окрашиваем все подокна в цвет ближайших к наблюдателю многоугольников (рис. 3.4). В данном варианте используются очень простой метод разбиения и критерий определения простоты визуализации, что приводит к большому количеству подразбиений. Для получения более эффективного алгоритма необходимо использовать более сложные методы и критерии. В случае простых сцен можно использовать прямоугольную оболочку (рис. 3.5). При этом окна подразбиения необязательно квадратные. Для более сложных сцен необходимо определить способы расположения многоугольников относительно окна. Многоугольник является: · внешним, если он находится вне окна (рис. 3.6, а); · внутренним, если он находится внутри окна (рис. 3.6, б); · пересекающим, если он пересекает окно (рис. 3.6, в); · охватывающим, если окно находится внутри него (рис. 3.6, г).
Рис. 3.2. Алгоритм отсечения Варнока
Рис. 3.3. Алгоритм отсечения Варнока.
Рис. 3.4. Алгоритм отсечения Варнока.
Рис. 3.5. Вариант разбиения в
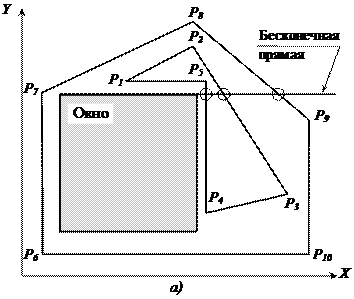
Рис. 3.6. Типы многоугольников И алгоритм удаления невидимых поверхностей будет заключаться в следующем: · если все многоугольники сцены являются внешними, то окно пусто и закрашивается цветом фона; · если внутри окна только один многоугольник, то он закрашивается своим цветом, остальное – фоном; · если только один многоугольник пересекает окно, то его часть, попадающая в окно, окрашивается цветом многоугольника, остальное – фоном; · если окно охвачено только одним многоугольником и в нем больше нет многоугольников, то окно окрашивается цветом этого многоугольника; · если окно охвачено несколькими многоугольниками, которые не протыкают друг друга, и в нем больше нет многоугольников, то окно окрашивается цветом ближайшего к наблюдателю многоугольника; · иначе – проводится разбиение окна. Аналогичным образом можно разработать правила и для алгоритма удаления невидимых линий: · если все многоугольники сцены являются внешними, то окно пусто и закрашивается цветом фона; · если внутри окна только один многоугольник, то рисуется его внешняя граница, остальное закрашивается фоном; · если только один многоугольник пересекает окно, то рисуется часть его внешней границы, попадающая в окно, остальное окрашивается фоном; · если окно охвачено одним или несколькими многоугольниками и в нем больше нет многоугольников, то окно окрашивается фоном; · иначе – проводится разбиение окна. Для реализации этих правил необходимы методы определения положения многоугольника относительно окна. В случае прямоугольных окон можно воспользоваться минимаксными (габаритными) тестами (рис. 3.7). То есть, если Xl, Xr, Yu, Yd – четыре ребра окна, а Xmax, Xmin, Ymax, Ymin – ребра прямоугольной оболочки, то этот многоугольник будет: - внешним, если: Xmin > Xr или Xmax < Xl или Ymin > Yu или Ymаx > Yd; - внутренними, если: Xmin ≥ Xl & Xmax ≤ Xr & Ymin ≥ Yd & Ymаx ≤Yu. Следующий способ – подстановка для проверки пересечения окна отсечения многоугольником. Координаты вершины окна подставляются в тестовую функцию, заданную уравнением прямой, несущей ребро многоугольника (Y = kX + b). Если знак этой тестовой функции не зависит от значений координат вершин окна, то все вершины многоугольника лежат по одну сторону от несущей прямой и на указанной прямой нет точек пересечения. Если эти значения различны, то многоугольник, возможно, пересекает окно. Если ни одно из ребер не пересекает окно, то этот многоугольник является либо внешним, либо охватывает окно. Уравнение тестовой функции для прямой, проходящей через вершины P1 и P2, имеет вид: Test Function = Y – kX - b, где k = (Y2 - Y1)/(X2 - X1), при X2 ≠ X1, b = Y1 - kX1 и Test Function = X - X1 при X2 = X1. Простым габаритным тестом нельзя идентифицировать все виды многоугольников, например, внешние многоугольники (рис. 3.6, а) или охватывающие многоугольники (рис. 3.6, г). Следовательно, здесь необходимо применять более сложные тесты. В приведенных ниже тестах предполагается, что были идентифицированы внутренние и пересекающие многоугольники. Остается определить внешние и охватывающие многоугольники.
Рис. 3.7. Проверка с помощью прямоугольной оболочки Тест с бесконечной прямой: - проводится луч из любой точки окна в бесконечность (обычно, используется одно из ребер окна) и подсчитывается число пересечений этого луча с заданным многоугольником (рис. 3.8, а), касание вершины равно 2, если вершина – локальный максимум или минимум, иначе - 1 (рис. 3.8, б). Касание стороны равно 2. Если сумма пересечений четная (или равна 0), то многоугольник внешний, иначе, он охватывает окно. Тест с подсчетом угла: - совершается обход ребер многоугольника по или против часовой стрелке. Суммируются углы, образованные векторами, начинающимися в любой точке окна и проходящими через начало и конец проходимого в данный момент ребра многоугольника (рис. 3.9). Если сумма углов равна 0, то многоугольник внешний, если сумма углов равна ±360*n, то многоугольник охватывает окно. На практике нет необходимости точно вычислять углы (да это и невозможно). Как и в случае алгоритма Коэна-Сазерленда, пространство изображения разбивается на 9 частей (рис. 3.10). Внешние октанты нумеруются от 0 до 7. Число целых октантов, покрытых углом равно ∆α = (№ октанта со вторым концом ребра) – (№ октанта с первым концом ребра). Предлагается следующий алгоритм: - если ∆α > 4, то ∆α = ∆α – 8; - если ∆α < - 4, то ∆α = ∆α + 8. Суммируя все ∆α, получаем: - если сумма ∆α равна 0, то многоугольник внешний по отношению к окну; - если сумма ∆α равна ±8*n, то многоугольник охватывает окно. Используя иерархически все вышеизложенные методы (и еще более сложные), мы получим алгоритм. Простейшая реализация алгоритма Варнока изложена в [1].
Рис. 3.8. Тест с бесконечной прямой
Рис. 3.9. Тест с подсчетом угла
Рис. 3.10. Модифицированный тест с подсчетом угла 
12 Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|








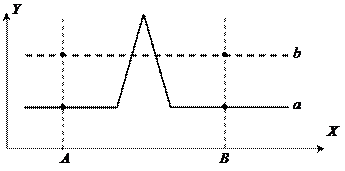







 Существует множество реализаций алгоритма Варнока, в том числе, работающих попеременно в пространствах изображения и объекта. Конкретная реализация зависит от метода разбиения окна и от критерия, используемого для решения вопроса о «простоте» окна.
Существует множество реализаций алгоритма Варнока, в том числе, работающих попеременно в пространствах изображения и объекта. Конкретная реализация зависит от метода разбиения окна и от критерия, используемого для решения вопроса о «простоте» окна.