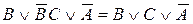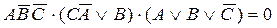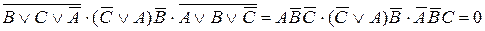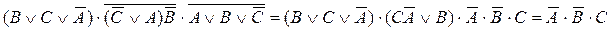|
|
Равносильности, выражающие основные законы алгебры логики
Следует отметить, что между равносильностями, записанными в дизъюнктивной форме и в конъюнктивной форме, существует свойство симметрии: если дизъюнкцию заменить конъюнкцией, а конъюнкцию заменить дизъюнкцией, 0 заменить на 1, а 1 заменить на 0, при этом отрицания сохранить без изменений, то записанные слева и справа равносильности перейдут друг в друга. Следовательно, с помощью указанных замен можно из одних равносильностей получить другие. Это называется законом двойственности.
Следствия алгебры логики. Многие законы можно обобщить на случай большого числа переменных. 1. Законы де Моргана в обобщенной форме можно записать так:
и 2. Законы дистрибутивности для многих переменных: AÚB×C×D×…×P = (AÚB)×(AÚC)×(AÚD)× … ×(AÚP) и A×(BÚCÚDÚ…ÚP) = A×BÚA×CÚA×DÚ…ÚA×P или
3. Законы поглощения для нескольких переменных: АÚ A×B Ú A×B×С×D = A; A×(AÚCÚDÚ…ÚP) = A;
Из симметрии трехчлена вида a) Если одна из переменных входит в одну из трех конъюнкций с отрицанием, то Заметим, что здесь симметрия нарушена по B. И конъюнкция, не содержащая этого “нарушителя симметрии ” поглотилась согласно закону поглощения (4). b) Если симметрия нарушена по двум переменным, например, имеем трехчлен вида
Пример. Упростить выражение Решение.Упростим выражения в скобках:
1. Перемножим полученные выражения.
2. Таким образом,
Нормальные формы логических выражений.Одна и та же логическая функция может быть записана различным образом. Например, функция F(A,B) может быть записана следующими эквивалентными выражениями: F(A,B)= Эквивалентность этих формул легко проверить по таблицам истинности или выполнив необходимые преобразования. Для исключения неоднозначности записи логические функции представляют в унифицированных формах. Такими формами являются: дизъюнктивная и конъюнктивная. В них используются элементарные дизъюнкции и конъюнкции. Эти формы часто используются и в представлении логических формул для построения по ним логических электронных схем, а также они полезны при решении текстовых задач, когда требуется представить полученное логическое выражение в определенной (нормальной) форме. Вначале дадим два определения: Элементарной дизъюнкцией называется дизъюнкция, состоящая только из переменных или их отрицаний. Например, Элементарной конъюнкциейназывается конъюнкция, состоящая только из переменных или их отрицаний. Например, 1. Дизъюнктивно нормальная форма (ДНФ): дизъюнкция элементарных конъюнкций. Например, 2. Конъюнктивно нормальная форма (КНФ): конъюнкция элементарных дизъюнкций. Например, 3. Минимальная дизъюнктивно-нормальная форма (МДНФ): ДНФ, имеющая самую короткую запись. 4. Минимальная конъюнктивно нормальная форма (МКНФ): КНФ, имеющая самую короткую запись. Использование нормальных форм не устраняет полностью неоднозначности записи логических функций. Например,
Поэтому среди нормальных форм выделяют такие, в которых функции записываются единственным образом. Их называют совершенными. Применяются совершенная дизъюнктивная и совершенная конъюнктивная формы (СДНФ и СКНФ), которые имеют отличительные особенности: 5. Совершенная дизъюнктивно нормальная форма (СДНФ): ДНФ, удовлетворяющая условиям: · Все элементарные конъюнкции различны; · Нет нулевых конъюнкций; · Ни одна из элементарных конъюнкций не повторяется; · Каждая элементарная конъюнкция содержит все переменные или их отрицания. 6. Совершенная конъюнктивно нормальная форма (СДНФ): КНФ, удовлетворяющая условиям: · Все элементарные дизъюнкции различны; · Нет нулевых дизъюнкций; · Ни одна из элементарных дизъюнкций не повторяется; · Каждая элементарная дизъюнкция содержит все переменные или их отрицания. Совершенная дизъюнктивная и совершенная конъюнктивная формы используются при проектировании элементов и узлов компьютера. Поскольку при проектировании отдельных узлов компьютера необходимо решить проблему построения логических и электрических схем, имея лишь описание алгоритма его работы (виде таблицы истинности или логической формулы). Воспользовавшись этими данными можно построить логическую, а затем электрическую или электронную схемы. Рассмотрим построение логической функции по известной таблице истинности.
Пусть необходимо получить логическую формулу, которая бы отвечала следующей таблице истинности. Зададимся вопросом, в какой форме удобнее искать логическую формулу, отвечающую заданной таблице истинности? Для однозначности описания состояния входных переменных наилучшим образом подходит совершенная форма, т.к. только в ней присутствует информация о каждой логической переменной, что соответствует таблице истинности. Иначе говоря, функция принимает единичные значения при наборах входных переменных, соответствующих 0, 3 и 7. Анализируя приведенную таблицу, заметим, что она содержит три строки, где функция F=1 и пять строк, где функция равна нулю. Для обеспечения состояний логического устройства, где F=1 воспользуемся построением логической формулы в виде СДНФ следующим образом. Для обеспечения единичного значения функции при А=0, В=0 и С=0 СДНФ должна иметь вид 1. Правило записи СДНФ функции по таблице истинности. Для всех наборов переменных, на которых функция принимает единичные значения, записываются конъюнкции этих переменных, инвертируя те переменные, которым соответствуют нулевые значения. Затем конъюнкции соединяют знаком дизъюнкции. Например, дана таблица истинности функции F:
СДНФ функции F будет состоять из двух наборов: По аналогичным соображениям строится логическая функция, соответствующая заданной таблице истинности. Учитывая свойство двойственности, правило записи СКНФ можно сформулировать следующим образом. 2. Правило записи СКНФ функции по таблице истинности. Для всех наборов переменных, на которых функция принимает нулевые значения, записываются конъюнкции этих переменных, инвертируя те переменные, которым соответствуют единичные значения. Затем дизъюнкции соединяют знаком конъюнкции. СКНФ функции F из предыдущего примера будет:
Решение текстовых задач. Для успешного решения текстовых задач необходимо знать, как записываются. Составим для себя таблицу соответствия высказываний естественного языка и формул алгебры логики. При решении текстовых задач желательно обходиться минимальным количеством переменных. Поэтому высказывания альтернативного типа, например "Погода пасмурная" и "Погода ясная", следует обозначать одной переменной, соответственно П и Задача. В олимпиаде по информатике участвовали трое друзей: А, В и С. Перед олимпиадой каждый из них высказал свои предположения. A: Не может быть, чтобы победили В и С вместе. Не может быть также, чтобы победил либо В, либо С. Значит, не могу победить и я. В: Если победит С, то победит и А, а я победить не смогу. С: Не может быть, чтобы не победили А и В, я бы победил. По результатам олимпиады оказалось, что прав был только один из друзей. Кто победил в олимпиаде? Чье высказывание оказалось правдой?
Решение. 1. Обозначим переменные: A - "Победил А", В - "Победил В", С - "Победил С". 2. Запишем высказывания друзей на языке алгебры логики и упростим их. A: = В: С: 1. Возможны три ситуации, когда прав лишь один из друзей. Пусть не правы А и В:
= Пусть не правы А и С:
Пусть не правы В и С:
Ответ: Победил С, правильное предположение сделал А.
Контрольные задания 1. Задано двоичное число 1101. На какое наименьшее двоичное число его необходимо умножить, чтобы результатом в десятичной системе счисления было число 19? Если решения нет, то в ответе записать 0, в противном случае запишите это число в двоичной системе счисления. 2. Даны три числа в различных системах счисления: A=16(10), B=21(8), C=12(10). Выполните следующие логические операции: AB+C. Ответ напишите в шестнадцатеричной системе счисления и в десятичной системе. 3. Постройте таблицу истинности для логической функции
4. Построить логическую функцию по заданной таблице истинности, которая имеет нулевые значения при следующих наборах переменных A, B, C: (001), (010), (011), (110). 5. Является ли данная функция тождественно ложной? 1) 2) 3) 4) 5) 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|


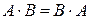

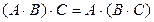
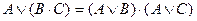




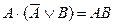
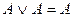


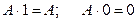
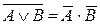

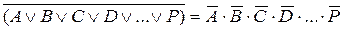
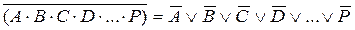
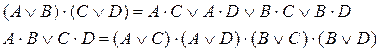 .
. ;
;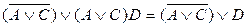 .
. получим полезные эквивалентности:
получим полезные эквивалентности: .
. , то его можно упростить следующим образом:
, то его можно упростить следующим образом: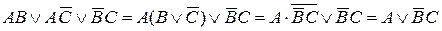 .
. .
.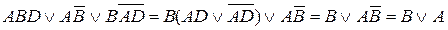
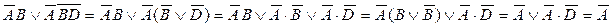

 .
. или F(A,B)=
или F(A,B)= 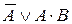 или F(A,B)=
или F(A,B)= 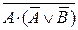 .
.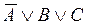 .
.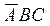 .
. .
.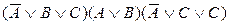 .
. может быть записана такими выражениями:
может быть записана такими выражениями: или
или  .
. , при значения А=0, В=1 и С=1 (четвертая строка), значение F=1 даст
, при значения А=0, В=1 и С=1 (четвертая строка), значение F=1 даст 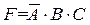 . Аналогично для последней строки –
. Аналогично для последней строки – 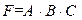 . Следовательно, для получения общей формулы, удовлетворяющей каждой из выделенных строк, необходимо взять дизъюнкцию этих трех конъюнкций и общая формула будет иметь вид
. Следовательно, для получения общей формулы, удовлетворяющей каждой из выделенных строк, необходимо взять дизъюнкцию этих трех конъюнкций и общая формула будет иметь вид 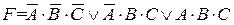 .
.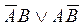 .
.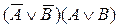 .
. .
.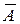
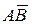
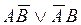
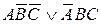

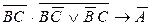 =
=  =
= 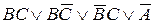 =
= =
=