
|
|
Равносильные формулы алгебры логики.Лекция 4. Элементы математической логики Логика в информатике — это направления исследований и отраслей знания, где логика применяется в информатике и искусственном интеллекте. Логика очень эффективна в этих областях. Алгебра логики (алгебра высказываний) — раздел математической логики, в котором изучаются логические операции над высказываниямиhttp://ru.wikipedia.org/wiki/%D0%90%D0%BB%D0%B3%D0%B5%D0%B1%D1%80%D0%B0_%D0%BB%D0%BE%D0%B3%D0%B8%D0%BA%D0%B8 - cite_note-1. Чаще всего предполагается, что высказывания могут быть только истинными или ложными (т.н. бинарная или двоичная логика, в отличие от, например, троичной логики, когда есть три варианта истинности высказывания: «истина», «ложь» и «не определено»). Логика высказыванийпослужила основным математическим инструментом при создании компьютеров. Она легко преобразуется в битовую логику: истинность высказывания обозначается одним битом (0 — ЛОЖЬ, 1 — ИСТИНА); тогда операция
Эту идею впервые реализовал английский математик Дж. Буль (1815 – 1864г.). Буль создал алгебру, в которой буквами обозначены высказывания, и это привело к алгебре высказываний. Именно благодаря введению символов в логику была получена основа для создания новой науки – математической логики. Задачей логики является изучение правильных способов рассуждений – таких способов рассуждений, которые приводят к верным результатам в тех случаях, когда верны исходные посылки. С помощью этой «грамматики» мы можем проверить правильность наших рассуждений. У логики много и других задач. Логика нужна, например, при анализе смысла отдельных утверждений, получении вывода. Ведь каждая мысль выражается с помощью соответствующего предложения – соответствующего высказывания. Высказывание – это повествовательное предложение, которому можно поставить в соответствие одно из двух значений – истина или ложь. Алгебра логики находит непосредственное и широкое применение при разработке средств электронной и вычислительной техники, о чем будет сказано в следующем разделе. Определения Базовыми элементами, которыми оперирует алгебра логики, являются высказывания. Высказывания строятся над множеством {B,
а также константы — логический ноль 0 и логическая единица 1. Логические операции Простейшим и наиболее широко применяемым примером такой алгебраической системы является множество B, состоящее всего из двух элементов: B = {Ложь, Истина} Как правило, в математических выражениях Ложь отождествляется с логическим нулём, а Истина — с логической единицей, а операции отрицания (НЕ), конъюнкции (И) и дизъюнкции (ИЛИ) определяются в привычном нам понимании. Легко показать, что на данном множестве B можно задать четыре унарные и шестнадцать бинарных отношений и все они могут быть получены через суперпозицию трёх выбранных операций. Опираясь на этот математический инструментарий, логика высказываний изучает высказывания и предикаты. Также вводятся дополнительные операции, такие как эквиваленция Рассмотрим логические операции над высказываниями. Отрицание. Отрицанием высказывания А называется новое высказывание, которое является истинным, если высказывание А ложно, и ложным, если высказывание А истинно. Обозначается отрицание
Конъюнкция(логическое умножение).Конъюнкцией двух высказываний А, В называется новое высказывание, которое считается истинным, если оба высказывания А, В истины, и ложным, если хотя бы одно из них ложно. Обозначается конъюнкция по-разному. Например, А´B, AB, АÙВ, А&B, А×B, читается “А и В”. Логические значения конъюнкции описываются следующей таблицей истинности:
Импликация. Импликацией двух высказываний A, B называется новое высказывание, которое считается ложным, если A истинно, а B - ложно, и истинным во всех остальных случаях.
Логические значения операции импликации описываются следующей таблицей истинности: Употребление грамматической связки «если..., то...» в математической логике отличается от употребления их в обычной речи, где мы, как правило, считаем, что если высказывание A ложно, то высказывание «Если A, то B» вообще не имеет смысла. Кроме того, строя предложение вида «если A, то B» в обыкновенной речи, мы всегда подразумеваем, что предложение B вытекает из предложения A. Употребление грамматической связки «если..., то...» в математической логике не требует этого, поскольку в математической логике смысл высказываний не рассматривается, а рассматривается лишь их логическое значение. Эквиваленция. Эквиваленцией (или эквивалентностью) двух высказываний А, В называется новое высказывание, которое считается истинным, когда оба высказывания А, В либо одновременно истинны, либо одновременно ложны, и ложным во всех остальных случаях. Эквиваленция высказываний А, В обозначается символом А«В, читается «для того, чтобы В, необходимо и достаточно, чтобы А», или «А тогда и только тогда, когда В». Логические значения операции эквиваленции описываются следующей таблицей истинности:
Эквивалентность играет важную роль в математических доказательствах. Известно, что значительное число теорем математики формулируется в форме необходимых и достаточных условий, то есть в форме эквивалентности. В этом случае, зная об истинности или ложности одного из двух элементов эквивалентности и доказав истинности самой эквивалентности, мы заключаем об истинности или ложности второго члена эквивалентности.
Пример. Пусть А - высказывание «Вася изучает программирование», В - высказывание «Вася любит математику». Рассмотрим словесную формулировку высказываний: 1) АÚВ; 2) Решение: 1) «Вася изучает программирование или любит математику». 2) «Вася не изучает программирование и не любит математику». 3) «Если Вася изучает программирование, то он любит математику». 4) «Неверно, что если Вася изучает программирование, то он любит математику». Остальные задания предлагается читателю записать самостоятельно.
Формулы алгебры логики. С помощью логических операций над высказываниями из заданной совокупности высказываний можно строить различные сложные высказывания. При этом порядок выполнения операций указывается скобками или операции выполняются согласно определенному приоритету. Например, из трех высказываний А, В, С можно построить высказывания Для упрощения записи формул принят ряд соглашений. Скобки можно опускать, придерживаясь следующего порядка действий: конъюнкция выполняется раньше, чем все остальные операции, дизъюнкция выполняется раньше, чем импликация и эквивалентность. Если над формулой стоит знак отрицания, то скобки тоже опускаются, т.е. при выполнении операций алгебры логики соблюдаются следующие приоритеты: 1. Выполнение операций в скобках 2. Операция логического отрицания. 3. Операция логического умножения 4. Операция логического сложения. 5. Операция импликации. 6. Операция эквивалентности. Операции с равным приоритетом выполняются слева направо. В связи с этим формулы Логическое значение формулы алгебры логики полностью определяется логическими значениями входящих в нее элементарных высказываний. Все возможные логические значения формулы, в зависимости от значений входящих в нее элементарных высказываний, могут быть описаны полностью с помощью таблицы истинности. Например, для формулы
Легко видеть, что если формула содержит n элементарных высказываний, то она принимает 2n значений, состоящих из нулей и единиц, или, что то же, ее таблица истинности содержит 2n строк. Так, для формулы, содержащей три переменные, таблица истинности будет иметь 23 = 8 строк, и формула принимает 8 значений, состоящих из нулей и единиц. Например, для формулы
Равносильные формулы алгебры логики. Две формулы алгебры логики А и В называются равносильными, если они принимают одинаковые логические значения на любом наборе значений элементарных высказываний, входящих в формулу. Запись A=B означает, что формулы А и В равносильны. Например, очевидно, что равносильны формулы: Х=X; Х&Х=X; Х&0=0; ХÚ1=1; ХÚ Легко видеть, что если А = В, то Формула А называется тождественно истинной (или тавтологией), если она принимает значение 1 при всех значениях входящих в нее переменных. Например, тождественно истинной является формула X®(Y®X), что можно проверить, построив таблицу истинности. Формула называется тождественно ложной, если она принимает значение ноль при всех значениях входящих в нее переменных. Как уже отмечалось Из определения равносильных формул следует, что отношение равносильности обладает свойствами: 1. А=А (рефлексивно); 2. Если A=В, то B=A (симметрично); 3. Если А=В и B=С, то A=С (транзитивно). Между понятиями равносильности и эквивалентности существует следующая связь: если формулы А и В равносильны, то формула А«В тавтология (то есть тождественно истинная), и, обратно, если формула А«В тавтология, то формулы А и В равносильны. Действительно, пусть А=В. Тогда эти формулы принимают одинаковые логические значения на любом наборе значений элементарных высказываний, входящих в формулы и, значит, формула А«В тождественно истинна. Очевидна справедливость и обратного утверждения. Равносильности, выражающие одни логические операции через другие:
Ясно, что равносильности 5 и 6 получаются из равносильностей 3 и 4 соответственно, если от обеих частей равносильностей 3 и 4 взять отрицания и затем воспользоваться законом двойного отрицания ( Так как при одинаковых логических значениях X и Y истинными являются формулы X«Y, X®Y, Y®X, то истинной будет и конъюнкция (X®Y)×(Y®X). Следовательно, в этом случае обе части равносильности 1 имеют одинаковые истинные значения. Пусть теперь X и Y имеют различные логические значения. Тогда будут ложными эквивалентность X«Y и одна из двух импликаций X®Y или Y®X. Но при этом будет ложной и конъюнкция (X®Y)×(Y®X). Таким образом, и в этом случае обе части равносильности 1 имеют одинаковые (ложные) значения. Рассмотрим равносильность 2. При Y =1, очевидно, что Пусть теперь Y = 0. Тогда при X =1, X®Y =0 и Рассмотрим равносильность 3. Если X и Y принимают одновременно истинные значения, то будет истинной конъюнкция X×Y и ложной отрицание конъюнкции В то же время будут ложными и Пусть теперь хотя бы одна из переменных X или Y принимает значение ложное. Тогда будет ложна конъюнкция X×Y и истинной ее отрицание. В то же время отрицание хотя бы одной из переменных будет истинным, а поэтому будет истинной и дизъюнкция Следовательно, во всех случаях обе части равносильности 3 принимают одинаковые значения. Аналогично доказывается равносильность 4. Из приведенных равносильностей следует, что всякую формулу алгебры логики можно заменить равносильной ей формулой, содержащей только две логических операции: конъюнкцию и отрицание или дизъюнкцию и отрицание. В самом деле, равносильность 1 позволяет заменить эквивалентность на импликацию и конъюнкцию, равносильность 2 позволяет заменить импликацию на дизъюнкцию и отрицание. Таким образом, после указанных замен в формуле будут использоваться только три операции: конъюнкция, дизъюнкция и отрицание. Если далее воспользоваться равносильностью 5, заменяя конъюнкцию на дизъюнкцию и отрицание, то в формуле будут использоваться только две операции: дизъюнкция и отрицание. Аналогично, если воспользоваться равносильностью 6, то в формуле останется также две операции: конъюнкция и отрицание. Дальнейшее исключение логических операций невозможно. Однако существуют операции, через которые может быть выражена любая из пяти логических операций, которыми мы пользуемся. Такой операцией является, например, операция «штрих Шеффера». Эта операция обозначается символом X|Y и определяется следующей таблицей истинности.
Очевидно, что имеют место равносильности: Из этих двух равносильностей следует, что всякая формула алгебры логики может быть заменена равносильной формулой, содержащей только операцию «штрих Шеффера». Отметим, что X|Y = Аналогично операции «штрих Шеффера» может быть использована операция, называемая «стрелкой Пирса»:

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
 приобретает смысл вычитания из единицы;
приобретает смысл вычитания из единицы; 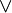 — немодульного сложения; & — умножения;
— немодульного сложения; & — умножения; 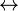 — равенства;
— равенства; 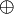 — в буквальном смысле сложения по модулю 2 (исключающее Или — XOR);
— в буквальном смысле сложения по модулю 2 (исключающее Или — XOR);  — непревосходства суммы над 1 (то есть A
— непревосходства суммы над 1 (то есть A  Историческая справка. Начало исследований в области формальной логики было положено греческим философом Аристотелем, который жил в 384-322 гг. до н.э. Он систематизировал известные до него сведения, и эта система стала впоследствии называться формальной логикой. Формальная логика просуществовала без серьезных изменений более двадцати столетий. Однако развитие математики, в которой широко используются логические построения, стимулировала и совершенствование формальной логики Аристотеля. Впервые перевести логику на язык математики предложил немецкий математик Г. Лейбниц в конце ХVII века. Он считал, что основные понятия логики должны быть определены правилами, и это позволит всякие рассуждения заменить вычислениями.
Историческая справка. Начало исследований в области формальной логики было положено греческим философом Аристотелем, который жил в 384-322 гг. до н.э. Он систематизировал известные до него сведения, и эта система стала впоследствии называться формальной логикой. Формальная логика просуществовала без серьезных изменений более двадцати столетий. Однако развитие математики, в которой широко используются логические построения, стимулировала и совершенствование формальной логики Аристотеля. Впервые перевести логику на язык математики предложил немецкий математик Г. Лейбниц в конце ХVII века. Он считал, что основные понятия логики должны быть определены правилами, и это позволит всякие рассуждения заменить вычислениями.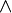 ,
, 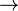 («следовательно»), сложение по модулю два
(«следовательно»), сложение по модулю два 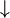 и другие.
и другие.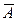 или Ø А и читается “не А” или “неверно, что А”. Логические значения высказываний
или Ø А и читается “не А” или “неверно, что А”. Логические значения высказываний 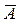 можно описать с помощью таблицы истинности, где 0 означает ложь, а 1 – истину. Таблица истинности для отрицания имеет вид:
можно описать с помощью таблицы истинности, где 0 означает ложь, а 1 – истину. Таблица истинности для отрицания имеет вид: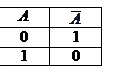 Если А высказывание, то
Если А высказывание, то 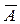 также является высказыванием, следовательно можно образовать отрицание и от
также является высказыванием, следовательно можно образовать отрицание и от 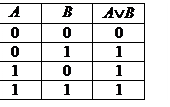 Дизъюнкция (логическое сложение). Дизъюнкцией двух высказываний A, B называется новое высказывание, которое считается истинным, если хотя бы одно из высказываний истинно, и ложным, если они оба ложны. Дизъюнкция высказываний A, B обозначается символом А Ú В, читается «A или B». Высказывания A, B при этом называются членами дизъюнкции. Логические значения дизъюнкции описываются следующей таблицей истинности:
Дизъюнкция (логическое сложение). Дизъюнкцией двух высказываний A, B называется новое высказывание, которое считается истинным, если хотя бы одно из высказываний истинно, и ложным, если они оба ложны. Дизъюнкция высказываний A, B обозначается символом А Ú В, читается «A или B». Высказывания A, B при этом называются членами дизъюнкции. Логические значения дизъюнкции описываются следующей таблицей истинности: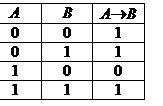 Импликация высказываний A, B обозначается символом A®B, читается «Если A, то B» или «из A следует B». При этом высказывание A называется условием или посылкой, высказывание В – следствием или заключением, высказывание А®В следованием или импликацией.
Импликация высказываний A, B обозначается символом A®B, читается «Если A, то B» или «из A следует B». При этом высказывание A называется условием или посылкой, высказывание В – следствием или заключением, высказывание А®В следованием или импликацией.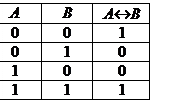 Например, высказывание «Треугольник АВС с вершиной в точке С и основанием АВ равнобедренный тогда и только тогда, когда ÐA = ÐB » является истинным, так как высказывания «Треугольник АВС с вершиной в точке С и основанием АВ равнобедренный» и «В равнобедренном треугольнике АВС с вершиной в точке С и основанием АВ ÐA = ÐB» либо одновременно истинны, либо одновременно ложны.
Например, высказывание «Треугольник АВС с вершиной в точке С и основанием АВ равнобедренный тогда и только тогда, когда ÐA = ÐB » является истинным, так как высказывания «Треугольник АВС с вершиной в точке С и основанием АВ равнобедренный» и «В равнобедренном треугольнике АВС с вершиной в точке С и основанием АВ ÐA = ÐB» либо одновременно истинны, либо одновременно ложны.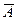 &
&  ; 3) A ® B; 4)
; 3) A ® B; 4) 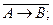 5)
5)  ; 6)
; 6) 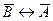 .
. и
и 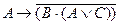 . Всякое простое высказывание и всякое сложное высказывание, которое может быть получено из элементарных высказываний посредством применения конечного числа логических операций отрицания, конъюнкции, дизъюнкции, импликации и эквивалентности, называется формулой алгебры логики.
. Всякое простое высказывание и всякое сложное высказывание, которое может быть получено из элементарных высказываний посредством применения конечного числа логических операций отрицания, конъюнкции, дизъюнкции, импликации и эквивалентности, называется формулой алгебры логики.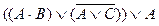 могут быть записаны так: А×ВÚ
могут быть записаны так: А×ВÚ  ÚА, а формула
ÚА, а формула 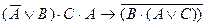 в виде
в виде 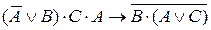 .
. таблица истинности имеет вид:
таблица истинности имеет вид: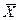

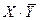
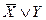
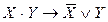
 таблица истинности имеет вид:
таблица истинности имеет вид:
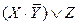
 =1; XÚХ=X; X&1=X; XÚ0=X; X&
=1; XÚХ=X; X&1=X; XÚ0=X; X& 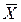 =0.
=0.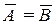 .
.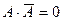 , то есть формула тождественно ложная.
, то есть формула тождественно ложная.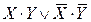 2. X®Y =
2. X®Y = 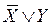 3.
3. 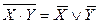 4.
4. 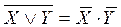 5.
5. 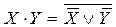 6.
6. 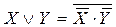
 ). Таким образом, в доказательстве нуждаются первые четыре равносильности. Докажем три из них: первую, вторую и третью.
). Таким образом, в доказательстве нуждаются первые четыре равносильности. Докажем три из них: первую, вторую и третью. = 1 и X®Y = 1, то есть обе части равносильности 2 имеют одинаковые значения.
= 1 и X®Y = 1, то есть обе части равносильности 2 имеют одинаковые значения.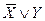 = 0, а при X = 0 X®Y = 1 и
= 0, а при X = 0 X®Y = 1 и 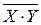 .
. , а поэтому будет ложной и дизъюнкция
, а поэтому будет ложной и дизъюнкция  .
. .
. =X|X, X×Y=(X|Y)|(X|Y).
=X|X, X×Y=(X|Y)|(X|Y).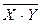 .
. .
.