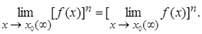Асимптоты графика функции

Графики и свойства основных элементарных функций.

Свойства:

1.Четность и нечетность. Функция у = f(х) называется четной, если для любых значений х из область определения f(-х)= f(х)и нечетной, еслиf(-х) = - f(х). В противном случае функция у = f(х) называется функцией общего вида.

Например, функция у = х, является нечетной, так как f(-х) = - х = -f(х).

График четнойфункции симметричен относительно оси ординат, а график нечетной функции симметричен относительно начала координат.

2.Монотонность. Функция у = f(х) называется возрастающей (убывающей) на промежутке Х, если большему значению аргумента из этого промежутка соответствует большее (меньшее) значение функции.

Функции возрастающие и убывающие называются строго монотонными функциями.

Например, функция у = х, является возрастающей для всех хÎR.

3.Ограниченность.Функция у = f(х) называется ограниченной на промежутке Х, если существует такое положительное число М, что | f(х)| £ М для любого хÎ Х.

Например, функция у = sin х ограниченна на всей числовой оси, т.к. |sin х | £ 1 для любого хÎR.

4.Периодичность. Функция у = f(х) называется периодической с периодом Т ¹ 0, если для любых х из области определения функции f(х+Т) = f(х).

Например, функция у = sin х имеет наименьший положительный период Т = 2p, так как для любых х sin (х+2p) = sin х.

Основными элементарнымифункциями называются следующие функции:

степенная у = хⁿ, где nÎN;

показательная у = а^х, где а > 0, а ¹ 1;

логарифмическая у = log_ax ,где а > 0, а ¹ 1;

тригонометрические: у = sin x, y = cos x, y = tg x, y = ctg x.

Степенная функцияу = хⁿ, nÎNи её свойства ООФ -область определения функции; ОЗФ – область значения функции. a) n- нечетное число (y=x; y=x³) 1.ООФ - x Î(-∞ ,+∞ ) 2.ОЗФ - y Î(-∞ ,+∞ ) 3. нечетная : y(-x)=-x=-y(x) 4.монотонность: возрастает на (-∞ ,+∞ ) 5. не периодическая b) n- четное число (y=x²) 1.ООФ - x Î(-∞ ,+∞ ) 2.ОЗФ - y Î(0 ,+∞ ) 3. четная : y(-x)=(-x)²=x²=y(x) 4.убывает: (-∞ ,0 ); возрастает на (0 ,+∞ ) 5. не периодическая Степенная функцияу = х^-ⁿ, nÎNи её св-ва a) n- нечетное число (y=1/x ) 1.ООФ - x Î (-∞ ,0 )U (0 ,+∞ ) 2.ОЗФ - y Î (-∞ ,0 ) 3. нечетная : y(-x)=-1/x=-y(x) 4.монотонность: убывает на (-∞ ,0 )U(0 ,+∞ ) 5. не периодическая b) n- четное число (y=1/x²) 1.ООФ - x Î (-∞ ,0 )U (0 ,+∞ ) 2.ОЗФ - y Î(0 ,+∞ ) 3. четная : y(-x)=(-x)²=x²=y(x) 4.убывает: (0, +∞ ); возрастает на (-∞,0 ) 5. не периодическая

Предел функции

Предел функции в точке

— Число А называется пределом функции у = f(х) при х, стремящимся к х₀, если для любого, даже сколь угодно малого положительного числа e, найдется такое положительное число d ( зависящее от e), что для всех х , не равных х₀и удовлетворяющих условию

— | х- х₀| < d,

— верно неравенство:

— | f(x)– А | < e

— Этот предел функции обозначается:

Предел функции в бесконечности

— Число А называется пределом функции у = f (х) при х, стремящемся к бесконечности, если для любого, даже сколь угодно малого положительного числа e, найдется такое положительное число S ( зависящее от e), что для всех х таких, что |х| > S, верно

— неравенство: |f(x)–А|<e|

— Этот предел функции обозначается:

Основные теоремы о пределах. Асимптоты графика функции

— Теорема 1. Функция не может иметь более одного предела.

Теорема 2. Предел алгебраической суммы конечного числа функций равен такой же сумме пределов этих функций, т.е.

— Теорема 3. Предел произведения конечного числа функций равен произведению пределов этих функций, т.е.

— Следствие.1. Постоянный множитель можно выносить за знак предела, т.е.

— Следствие 2. Предел степени равен степени предела, т.е.

— Теорема 4. Предел частного двух функций равен частному пределов этих функций, при условии, что предел делителя не равен нулю, т.е.

Замечательные пределы

Асимптоты графика функции

— Асимптотой графика функции у =¦( х) называется прямая, обладающая следующим свойством, что расстояние от переменной точки на графике до этой прямой стремится к нулю при неограниченном удалении этой точки по графику от начала координат.

— Теорема 1. Пусть функция у = ¦( х) определена в некоторой окрестности точки х₀ (исключая, возможно, саму эту точку) и хотя бы один из пределов функции при х® х₀ – 0 (слева) или при х® х₀ + 0 (справа) – равен бесконечности, тогда прямая при х = х₀ является вертикальной асимптотой графика функции у = ¦( х).

— Замечание. Вертикальные асимптоты следует искать в точках разрыва функции у = ¦( х) или на концах ее области определения (а, b) если а и b - конечные числа.

— Теорема 2. Пусть функция у = ¦(х) определена при достаточно больших х и существует конечный предел функции при х ® ¥ и он равен числу b. Тогда прямая у = b есть горизонтальная асимптота графика функции у = ¦( х).

— Замечание. Если конечен лишь один из пределов слева или справа, то функция имеет лишь левостороннюю или правостороннюю асимптоту.

— Теорема 3. Пусть функция у = ¦( х) определена при достаточно больших х и существует конечные пределы

— Тогда прямая у = kx + b является наклонной асимптотой.

12 3 4 5

Не нашли, что искали? Воспользуйтесь поиском по сайту: