
|
|
Исходные данные выделены жирным шрифтом.
Изменение химического и фазового состава системы при протекании реакции влечет за собой изменение ее термодинамических характеристик и свойств. Текущее изменение энтальпии
выражается через стехиометрически определенную энергетическую характеристику реакции – энтальпию реакции Dr H. При определении энтальпии химического соединения Hi необходимо выбрать уровень ее отсчета. Для этой цели используется функция
которая в теплотехнической литературе получила название полной энтальпии. Кроме энтальпии нагревания от T0 до T (в квадратных скобках) она выражена через энтальпию образования химического соединения из простых веществ при T0. Комиссия ИЮПАК по термодинамике определила (1975 г.) в качестве основного стандартного состояния для газообразных веществ простое вещество в состоянии идеального газа с давлением Рº = 1 атм при любой фиксированной температуре. Для твердых и жидких веществ основное стандартное состояние – это состояние чистого вещества, находящееся под давлением Рº = 1 атм. Если специально не оговорено, принято T0 = 298,15 К. Все стандартные значения отмечаются маленьким кружочком в позиции верхнего индекса с указанием температуры в скобках. Стандартная энтальпия реакции общего вида 0 = Σνi Ai из формул (3.28), (3.29) выражается через стандартные энтальпии образования реагентов и продуктов Пример: CH4 + CO2 = 2 CO + 2 H2. DrH°(298) = -(-74,85) - (-393,51) + 2×(-110,5) + 2×(0) = 247,36 кДж/моль
В свою очередь, DfH°(298) химического соединения – это DrH°(298)образования моля этого соединения из простых веществ. Например: C, графит + 1/2 O2 = CO, DfH°(298) = –110,54 кДж/моль H2 + 1/2 O2 = H2O, ж DfH°(298, ж) = –285,84 КДж/моль
3.5.1. Зависимость теплового эффекта реакции от температуры можно получить, если формулу (3.29) с T0 = 298,15 К подставить в формулу (3.28):
Дифференциальная форма температурной зависимости энтальпии реакции носит название уравнения Кирхгоффа
Если в данном температурном интервале DrCР > 0, то при повышении температуры энтальпия возрастает, и наоборот. Ранее определив другую важнейшую функцию – энтропию, мы уже привели формулу (3.24), которая определяет стандартное ее значение по данным о теплоемкости и энтальпиям DtrH° фазовых и полиморфных превращений. Заменив букву H буквой S вместо формул (3.27) и (3.28) для энтальпии получаем пропорциональное координате реакции изменение энтропии системы, выраженное через энтропию реакции
В отличие от энергетических функций, 3-й закон термодинамики однозначно определяет нулевой уровень отсчета энтропии для каждого «нормального» вещества при 0 К. Наконец, стандартные энтальпия и энтропия составляют стандартную энергию Гиббса реакции – её важнейшую термодинамическую характеристику: DrG° = DrH° – TDrS°. (3.33)
3.6. Энтропия идеального газа и идеальной газовой смеси. Подставив дифференциал мольного объема Энтропийная постоянная идеального газа S′ при конкретизированных T1 = 1 К, P1 = P° = 101325 Па = 1 атм – это энтропия 1 моля газа при стандартном давлении P° и температуре 1 К может быть вычислена методами статистической термодинамики по молекулярным постоянным. Т. о. абсолютная энтропия моля идеального газа
где стоящие под знаком ln T = T/1К и
S(до смешения) = После разрушения перегородок и необратимого (диффузионного) смешения каждый из газов займет весь объем. При этом температура останется неизменной, поскольку внутренняя энергия газа не зависит от объема. Одинаковое и равное давление P после разрушения перегородок становится общим давлением Энтропия системы после смешения газов равна S(после смешения) = Изменение энтропии в результате смешения газов называют энтропией смешения DSсм = S(после смешения) – S(до смешения) : DSсм = Оказывается, что это выражение определяет энтропию смешения не только газовых, но и жидких и твердых идеальных растворов. При смешении компонентов энтропия системы необратимо возрастает. 3.7. Энергия Гиббса смеси. Химический потенциал компонента в растворе Определение основных понятий химической термодинамики и получение общих соотношений продолжим на примере идеально газовой системы. Энтальпию i-го компонента при (необязательном) условии постоянства Cp легко получить из её определения (3.19): Hi = CРi×T + H0i , (3.39) где H0i = U0i – внутренняя энергия моля идеального газа при 0 К. Составим из
Величина μi называется химическим потенциалом i‑го компонента в газовой смеси. Используя определение парциального давления которую можно применять уже не только к газовым, но и к конденсированным смесям. При протекании химических процессов происходит изменение состава реакционной смеси. Соответствующее изменение G:
Можно показать, что Являясь важнейшей характеристикой вещества в растворе, химический потенциал i‑го вещества - это, прежде всего, частная производная от энергии Гиббса по его мольному количеству в растворе. 3.8. Термодинамический закон действующих масс (ТЗДМ) Для химической реакции общего вида
По химическим потенциалам и стехиометрическим коэффициентам νi компонентов, аналогично энтальпии (3.28) и энтропии (3.28'), определена энергия Гиббса реакции
Равновесие в изобарно-изотермическом процессе, в соответствии условием (3.17), определяется нулевой скоростью изменения энергии Гиббса (3.43) в точке её минимума:
Это общее условие равновесия конкретизируем для газофазной реакции, подставив в него химические потенциалы (3.41) участников:
где - стандартная энергия Гиббса реакции. Преобразование и эспоненцирование (3.45') приводит к уравнению:
Не зависящая от состава реакционной смеси его левая часть называется стандартной константой равновесия:
Правую часть (3.46)
Уравнение, отражающее условие равновесия химической реакции, называется термодинамическим законом действующих масс (ТЗДМ). Форма (3.49) - для реакции общего вида, (3.49') - для 4-х компонентного уравнения реакции в обычной записи. Поскольку состав системы можно характеризовать разными концентрационными единицами, то различные, в общем случае размерные правые части ТЗДМ, слева должны уравниваться соответствующими константами равновесия. Подстановка связи
Здесь Dn = Sni = n3 + n4 – n'1 – n'2 – изменение числа молей в реакции, Kx, KP, Kc – константы равновесия, соответствующие использованию мольных долей xi, парциальных давлений Pi (атм) и концентраций ci (моль/м3). 3.9. Направление протекания химической реакции. Использование термодинамического закона действующих масс для расчета состава равновесной смеси Относительные парциальные давления компонентов реакции до момента их взаимодействия, т.е. в исходном состоянии, отметим дополнительным нижним индексом «0» и выразим энергию Гиббса реакции (3.44) из ТЗДМ (3.45'):
Выражение (3.51) впервые получено Вант-Гоффом, а Де-Донде, исходя из необходимого для самопроизвольного протекания процесса отрицательного значения · Если в исходном состоянии энергия Гиббса реакции: o o · Текущие концентрации будут изменяться до достижения своих равновесных значений при Расчет равновесного состава при фиксированных Т и Р и при заданной или вычисляемой по энергиям Гиббса веществ константе равновесия сводится к нахождению химической координаты реакции x. Для нескольких реакций вместо одного требуется решать уже систему уравнений ТЗДМ с привлечением специализированных компьютерных средств. Ниже представлено решение для простых, но практически важных реакций. Форма ТЗДМ (3.50х) соответствует мольным долям xi. Пример 1. Зависимость выхода йодистого водорода от соотношения реагентов.
xi = ni / Σni ; Для удобства введены обозначения:
Результаты вычислений при различных исходных количествах йода и водорода (n; m) показывают, что выход по йоду x/n можно повысить за счет избытка водорода!
Пример 2. Расчет выхода аммиака и его зависимость от давления.
Приемлемый выход можно достичь только при повышенных давлениях. На практике аммиак с 30 % -м выходом синтезируют при давлениях около 300 атм.
3.10. Влияние температуры и давления на химическое равновесие Зависимость константы равновесия от давления явным образом выражена для
Последнее равенство в (3.52) получено из уравнения Менделеева-Клапейрона. Анализ уравнения (3.52) показывает, что с увеличением общего давления реакционной смеси: 1) для реакций, сопровождающихся уменьшением числа молей и газового объема (Dn < 0 и DrV < 0) Kx возрастает, а равновесие смещается вправо, в сторону образования продуктов; 2) в противном случае (Dn > 0 и DrV > 0) – равновесие смещается влево, что делает реакцию менее выгодной. Влияние температуры на химическое равновесие вытекает из зависимости логарифма стандартной константы равновесия (3.47)
При выводе изобары (P = const) реакции Вант-Гоффа были использованы соотношения: G = H – TS и С увеличением температуры процесса, согласно (3.53): 1) для эндотермических (теплопоглощающих, DrH° > 0) реакций при положительной производной K° будет возрастать, а равновесие сдвигается вправо, в сторону целевых продуктов; 2) для экзотермических (тепловыделяющих, DrH° < 0) реакций равновесие сдвигается влево, в сторону исходных веществ.
Математически установленные количественные закономерности о влиянии T и P на качественном уровне могут быть интерпретированы на основании принципа смещения равновесия Ле Шателье (- Брауна). При нарушающем равновесие внешнем воздействии система переходит в такое состояние, при котором эффект этого воздействия ослабевает. Например, повышение температуры для эндотермической (теплопоглощающей) реакции смещает равновесие в сторону увеличения выхода её продуктов, а для экзотермической – в сторону регентов. Повышение давления смещает равновесие в сторону уменьшения объема, что нивелирует рост давления. Наконец, добавление реагента смещает равновесие в сторону, уменьшающую добавок.
3.11. Химическое равновесие в гетерогенных системах. Химические реакции, компоненты которых находятся в разных фазах, называются гетерогенными. Общая форма записи системы одновременно протекающих реакций химических реакций: Рассмотрим две реакции, которые занумерованы римскими цифрами. Компоненты отмечены арабскими цифрами сверху; (тв) и (г) - указатели твердой и газовой фаз. Ниже, под каждым компонентом записаны их химические потенциалы. Газообразным компонентам соответствует форма (3.41), а твердым форма (3.41'). x1 = 1 соответствует индивидуальному тв. веществу. 1 2 3 4 I. С(тв) + СО2(г) = 2 СО(г), II. С(тв) = С(г)
Повторение вывода ТЗДМ (3.46) для конкретных уравнений I и II даёт:
Стандартные константы равновесия гетерогенных реакций содержат химические потенциалы всех компонентов. Стехиометрическое произведение концентраций образовано только газообразными компонентами. Равновесный состав находится решением двух уравнений (3.54) с предварительным расчетом констант равновесия по данным Отметим, что второе уравнение (3.54) отражает только фазовое равновесие между твердым и газообразным углеродом.
Химическая кинетика Химическая кинетика вслед за термодинамикой, является теоретической основой химической технологии, тепловой энергетики, металлургии и др. Принципиальная возможность, направление и глубина протекания химической реакции определяются из анализа начального и конечного состояний по законам термодинамики, а кинетика выясняет реальную возможность и время достижения конечного состояния, в том числе, путем анализа промежуточных состояний. Например, исходная смесь H2 и O2, несмотря на чрезвычайную выгодность реакции H2 + O2 = H2O, DrG(298) = -229 кДж/моль, может существовать очень долго, однако мгновенно, с взрывом протекает при ее инициировании искрой. Термодинамический анализ реакции получения HJ позволил рассчитать выход продукта при 718 К, который при эквимолярном соотношении реагентов составил 77,2 % (см. пример 1 в разделе 3.9).
Кинетические измерения (Боденштейн) показали, что равновесное состояние достигается за время ~20 ч. При этом процесс взаимодействия водорода с йодом представляется совокупностью элементарныхреакций с их различным долевым участием, зависящим от температуры и соотношения реагентов. H2 = H˙ + H˙, J2 = J˙ + J˙, H˙ + J˙ = HJ, H˙ + J2 = HJ + J˙, J˙ + H2 = HJ + H˙ Кинетическое исследование процессов горения, например H2 в O2, и ряда других позволили Н.Н. Семенову разработать теорию цепных реакций, получить за это звание академика, а впоследствии и Нобелевского лауреата. Реакция образования воды из H2 и O2 при обычных условиях не происходит из-за высокой энергии активации (см. далее). Инициирование реакции зарождает цепь созданием активных радикальных частиц H·, OH·, O·: В результате элементарных реакций, составляющих звено цепи (ЗЦ), наряду с продуктом цепной реакции образуются новые радикалы.
Баланс между ростом числа радикалов и их гибелью на стенках, инертных частицах определяет скорость процесса, которая при малых потерях радикалов носит экспоненциальный, взрывной характер. Ядерная физика позаимствовала химические представления для цепной реакции деления ядер, условием возникновения которой является наличие размножающихся нейтронов. Скорость химической реакции по номенклатурным правилам IUPAC определяется как скорость возрастания химической координаты реакции x. Напомним, что для реакции общего вида Таким образом, скорость произвольной реакции:
где υi – скорость изменения количества i‑го компонента, моль/с. Для гомогенной (объемной) реакции используется отнесенная к единице объема V скорость r, которая связана с объемной концентрацией ci. При учете ni = ci×V
При постоянном объеме (V = const)
где компонентная скорость изменения концентрации ri > 0 для продуктов и ri < 0 для исходных веществ. Для элементарной реакции
определяет основной закон кинетики или кинетический закон действующих масс (КЗДМ): Скорость элементарной реакции пропорциональна произведению концентраций реагентов в степенях их стехиометрических коэффициентов. Коэффициент пропорциональности kназывается константой скорости. Коэффициенты n'i в КЗДМ – только целые числа 1, 2, 3. Впервые КЗДМ сформулирован Гульдбергом и Вааге в 1887 г. Для двусторонней обратимой реакции
где k+, k− - константы скорости прямой и обратной реакций. При достижении равновесия (r = 0)
отношение констант скоростей прямой и обратной реакций оказывается равным константе равновесия. Это позволяет по k+, рассчитывать k− и наоборот. На практике ni и n'i могут отличаться от стехиометрических коэффициентов, что объясняется не элементарностью и скрытой многостадийностью большинства химических реакций. По этой же причине порядок реакцииn = Sn'i не совпадает с величиной, найденной из обработки кинетических кривых. Объединение формул (3.57) и (3.58) дает дифференциальное уравнение, в данном случае односторонней реакции
В примерах решения или интегрирования этого уравнения для отыскания зависимостей с(t) (т.н. кинетических кривых) индексом “0” отмечены начальные концентрации реагентов.
Для сложных задач химической кинетики из нескольких совместно протекающих реакций созданы и создаются специальные компьютерные программы. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 (3.27)
(3.27)  (3.28)
(3.28) , (3.29)
, (3.29) . (3.30)
. (3.30)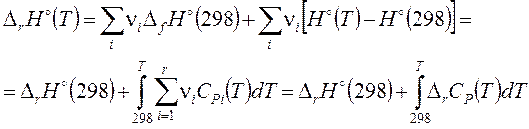
 . (3.32)
. (3.32) .
. ,
,  , (3.28')
, (3.28') идеального газа
идеального газа  в основное термодинамическое соотношение TdS = CV dT + РdV и использовав связь (3.20) CV = CP – R получаем
в основное термодинамическое соотношение TdS = CV dT + РdV и использовав связь (3.20) CV = CP – R получаем  . Интегрирование от T1 и P1 до Т и Р даёт
. Интегрирование от T1 и P1 до Т и Р даёт  .
. , (3.35)
, (3.35) - безразмерные величины.
- безразмерные величины.
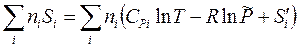 (3.36)
(3.36) , которое по закону Дальтона складывается из парциальных
, которое по закону Дальтона складывается из парциальных  , где
, где  - мольная доля i-гокомпонента в смеси.
- мольная доля i-гокомпонента в смеси. . (3.37)
. (3.37) . (3.38)
. (3.38) и S (3.37) энергию Гиббса G = H – TS =
и S (3.37) энергию Гиббса G = H – TS =  . Объединив все слагаемые
. Объединив все слагаемые  , которые зависят от природы i‑го вещества и температуры, но не зависят от состава смеси, получаем
, которые зависят от природы i‑го вещества и температуры, но не зависят от состава смеси, получаем , (3.40)
, (3.40) 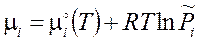 . (3.41)
. (3.41) - стандартный химический потенциал компонента при парциальном давлении
- стандартный химический потенциал компонента при парциальном давлении  .
. , из (3.41) получаем другую форму химического потенциала
, из (3.41) получаем другую форму химического потенциала 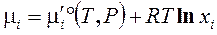 (
(  ), (3.41')
), (3.41') , (3.42)
, (3.42)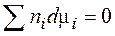 , а из (3.42) следует фундаментальное определение химического потенциала
, а из (3.42) следует фундаментальное определение химического потенциала 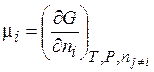 (3.41'').
(3.41'').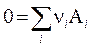 (для реагентов ni < 0) изменению состава компонентов
(для реагентов ni < 0) изменению состава компонентов  при постоянных Т и Р, согласно (3.42), соответствует дифференциальное, а затем и конечное изменение энергии Гиббса.
при постоянных Т и Р, согласно (3.42), соответствует дифференциальное, а затем и конечное изменение энергии Гиббса.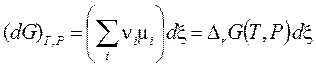 ,
, 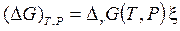 . (3.43)
. (3.43) . (3.44)
. (3.44) . (3.45)
. (3.45) ,
,  ,(3.45')
,(3.45') (3.44')
(3.44') (3.46)
(3.46) . (3.47)
. (3.47) назовем стехиометрическим произведением концентраций. В данном случае оно выражено через равновесные значения безразмерных парциальных давлений.
назовем стехиометрическим произведением концентраций. В данном случае оно выражено через равновесные значения безразмерных парциальных давлений. (
(  , νi < 0 для реагентов). (3.49)
, νi < 0 для реагентов). (3.49)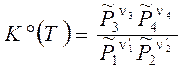 (n'1A1+ n'2A2 = n3A3 + n4A4). (3.49')
(n'1A1+ n'2A2 = n3A3 + n4A4). (3.49') с соответствующей концентрацией в (3.49) позволяет для каждой формы ТЗДМ выразить соответствующую константу равновесия через стандартную К°(Т).
с соответствующей концентрацией в (3.49) позволяет для каждой формы ТЗДМ выразить соответствующую константу равновесия через стандартную К°(Т). ,
,  ,
,  ; (3.50х)
; (3.50х)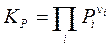 ,
,  ,
,  ; (3.50Р)
; (3.50Р) ,
,  ,
,  . (3.50с)
. (3.50с) (3.51)
(3.51) < 0, то x > 0 и реакция потечет слева направо.
< 0, то x > 0 и реакция потечет слева направо. = 0.
= 0. ;
;  .
. ,
,  , A=1−4/K.◦ Тогда
, A=1−4/K.◦ Тогда 
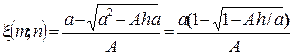
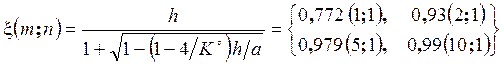

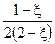

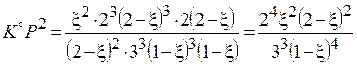 ,
, 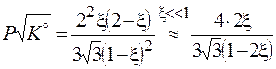
 .
.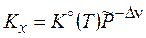 в (3.50x). Логарифмирование
в (3.50x). Логарифмирование  и дифференцирование по давлению дает:
и дифференцирование по давлению дает: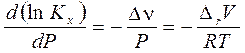 . (3.52)
. (3.52)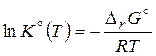 от температуры:
от температуры:
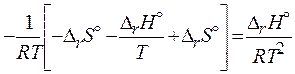 (3.53)
(3.53) в применении к реакции.
в применении к реакции. , j – номер реакции, p – указатель фазы i-го компонента.
, j – номер реакции, p – указатель фазы i-го компонента.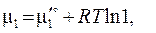
 ,
,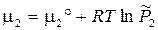 ,
, 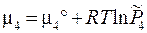
 .
. ,
,  .
.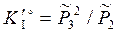 ,
,  . (3.54)
. (3.54)
 для каждого вещества.
для каждого вещества.
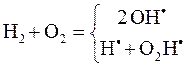
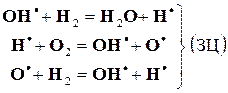
 (ni < 0 для реагентов), координата реакции имеет вид: x= (ni – ni0)/ni .
(ni < 0 для реагентов), координата реакции имеет вид: x= (ni – ni0)/ni . , (3.55)
, (3.55)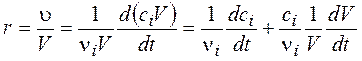 . (3.56)
. (3.56) ,
,  , (3.57)
, (3.57) выражение
выражение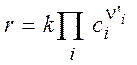 (3.58)
(3.58)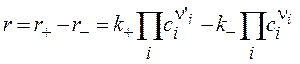 , (3.59)
, (3.59)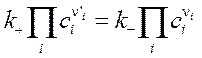
 (3.60)
(3.60) . (3.61)
. (3.61)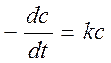 ,
,  ,
ln c – ln c0 = – kt, c = c0e–kt
,
ln c – ln c0 = – kt, c = c0e–kt
 ,
, 
