
|
|
Процессы, приводящие к уменьшению энтропии, в изолированных или замкнутых системах невозможны.Термическое равновесие (все части системы находятся при одинаковой температуре) есть необходимое условие термодинамического равновесия. Термическое уравнение состояния: V = f(T, P, ni), (3.1) например, V= (RT/P)Σni – для идеального газа. Калорическое уравнение состояния: U= f (T, V, ni)(3.1а) Термодинамика основана на установленных опытным путем законах, так называемых началах, откуда могут быть выведены все зависимости между термодинамическими величинами. Первое начало термодинамики(частный случай закона сохранения энергии): В закрытой системе изменение внутренней энергии ΔU равно разности теплоты Q, поглощенной системой из окружающей среды, и работы A, произведенной системой над окружением: ΔU = Q − A (3.2) Первое начало термодинамики исключает возможность создания вечного двигателя первого рода, который при помощи кругового процесса (ΔU = 0)совершал бы работу большую подводимой извне энергии в форме тепла (А = Q). Работа А в большинстве случаев совершается в форме работы расширения А = P ΔV. Дифференциальная форма 1-го начала для этого случая имеет вид: δQ = dU + P dV. (3.2')
Второе начало термодинамики взаимосвязано с определением энтропии. Её изменение ΔS выражается через поглощенную системой теплоту для обратимо протекающего процесса в закрытой системе: ΔS = В соответствующем необратимом процессе с присущими ему внутренними теплопотерями, в частности, на трение количество поглощенной и «усвоенной» системой теплоты будет меньше, а изменение энтропии от начального до конечного состояния будет больше соответствующего необратимому процессу интеграла: ΔS > Поскольку все процессы в природе в той или иной степени необратимы, то в изолированной системе ( Процессы, приводящие к уменьшению энтропии, в изолированных или замкнутых системах невозможны. Если к термодинамической системе, состоящей из огромного числа частиц, подходить с позиции вероятностных законов, то представляется очевидным, что любой самопроизвольный процесс протекает в направлении, при котором система переходит из менее вероятного в более вероятное состояние. Этот вывод может служить одной из формулировок второго начала термодинамики. Покажем, что статистическая формула Больцмана S = R×lnW, которая выражает энтропию через вероятность термодинамического состояния W,действительно соответствует определению энтропии через приведенную (т.е. деленную на температуру) теплоту dQ/T. Доказательство выполним для модели идеального газа, начав с вычисления теплоты, приобретенной системой при обратимом изотермическом (ΔU = 0, см. далее) расширении 1 моля идеального газа.
Очевидно, что чем больше объем V, тем больше вероятность нахождения в нем рассматриваемого моля газа. Заменяя отношение V2/V1 равным ему W2/W1 и сопоставляя деленное на Т соотношение (3.4) с вытекающим из формулы Больцмана изменением энтропии DS = S2 – S1 = R×ln(W2/W1), получаем DS = Qобр/T, которое соответствует определению (3.3). Далее, не сложно показать, что найденная работа обратимого изотермического расширения (3.4) всегда больше работы соответствующего необратимого процесса Анеобр = P (V2 – V1) = RT (V2 – V1)/V2 = RT (1 – V1/V2), (3.5) когда отпущенный при объёме V1 поршень первоначально сжатого в цилиндре газа в условиях постоянного внешнего давления P (возможно после нескольких колебаний) остановится в положении с объёмом V2. Неравенство вычисленных работ Аобр > Анеобр для рассмотренного идеального газа в изотермическом (ΔU = 0) процессе с учетом первого закона термодинамики приводит к неравенству Qобр > Qнеобр. Его деление на T дает неравенство ΔS > Qнеобр / T , (3.6) которое обосновывает принципиальную часть второго начала термодинамики (3.3'). Второе начало термодинамики исключает возможность создания вечного двигателя второго рода, т.е. устройства, в котором при помощи кругового процесса охлаждается источник тепла, причем все количество теплоты превращается в механическую работу. Возможно лишь частичное превращение теплоты в работу (в противоположность обратному процессу). Коэффициент полезного действия процесса, в котором происходит превращение теплоты в работу: Q1и Q2 – количества теплоты отданное нагревателем и поглощенное холодильником, находящимся, соответственно, при температуре Т1и Т2. Второе равенство в (3.7) справедливо для полностью обратимых процессов (например, для цикла Карно). Все естественные процессы (например, в тепловых машинах) протекают с меньшим коэффициентом полезного действия. Дифференциальная форма соотношения (3.6) после подстановки в него (3.2) объединяет 1-ое и 2-ое начала термодинамики: TdS > dU + PdV + δAнеобр. При этом в совершаемой системой общей работе по всем ее видам выделена работа расширения PdV. В окончательной форме основного термодинамического соотношения TdS ≥ dU + PdV +δA (3.8) знак равенства относится к обратимым процессам, а знак неравенства - к необратимым. В изолированной системе (dU = 0, dV = 0,δA= 0), т. е. при фиксированных U и V , как следует из (3.8), могут протекать процессы только с возрастанием энтропии: (dS)U,V ≥ 0 (3.9) В результате такого самопроизвольного процесса при рассматриваемых условиях (U, V = const) система приходит в состояние равновесия, а её энтропия достигает максимального значения. Соответствующие критерии равновесия в математической форме имеют вид: (dS)U,V = 0, (d 2S)U,V < 0 . (3.10) 3. 2. Характеристические функции Совершаемая системой работа А, при её выражении из основного термодинамического соотношения (3.8) δA ≤ TdS - dU - PdV (3.11) будет максимальной при обратимом процессе (знак равенства в (3.11)). Например, максимальную полезную работу в химической реакции можно получить, если проводить её в обратимом гальваническом элементе. Величина полезной работы будет зависеть от условий протекания реакции. 3.2.1. В самопроизвольном процессе при условии постоянства S, V (dS=0, dV=0),согласно (3.11), δA ≤ - (dU)S,V.Максимальная полезная работа равна убыли внутренней энергии системы U: (Aобр)S,V = - (ΔU)S,V = - (U2 – U1)S,V (3.12) Внутренняя энергия как характеристическая функция объема V и непосредственно не измеряемой энтропии S не удобна и редко используется в термодинамике для решения практических задач. 3.2.2. Для самопроизвольного процесса при постоянных S, Р из (3.11) следует δA ≤ (- dU - PdV)S,Р = − (dU + PdV)S,Р = − (dН)S,Р. (3.13) Максимальная полезная работа при данных условиях равна убыли энтальпии системы Н = U + PV. 3.2.3. Для самопроизвольного процесса при постоянных Р и Т соотношение (3.11) можно представить в виде δA ≤ − d(U + PV − TS)T,Р , (3.14) поскольку дифференциал в последнем выражении при постоянных Р и Т действительно соответствует (3.11). Функция G = U + PV – TS = H – TS (3.15) называется термодинамическим потенциалом Гиббса или энергией Гиббса. Для обратимого процесса при постоянных Р и Т максимальная полезная работа равна убыли этой важнейшей для химии термодинамической функции состояния. 3.3. Критерии возможности и направленности самопроизвольного процесса и условия равновесия Если направленность самопроизвольного процесса в изолированной системе определяется возрастанием энтропии (3.9), а равновесие – условиями её максимума (3.10), то для закрытых систем ответы на эти вопросы получают на основании величины полезной работы А > 0. Максимальная полезная работа при задаваемых условиях постоянства параметров процесса (нижние индексы) определяется убылью соответствующей функции состояния или соответствующего термодинамического потенциала: δA = - (dU)S,V , δA = - (dH)S,P , δA = - (dF)T,V , δA = - (dG)T,P . (3.16) Т. о. при самопроизвольном протекании физико-химического или химического процесса в закрытой системе соответствующие условиям процесса термодинамические потенциалы должны уменьшаться, достигая в равновесии минимальных величин, удовлетворяющих критериям равновесия: (dU)S,V = 0, (dH)S,P = 0, (dF)T,V = 0, (dG)T,P = 0; (3.17) (d 2U)S,V > 0, (d 2H)S,P >0, (d 2F)T,V >0, (d 2G)T,P >0. (3.18) К ранее введенным добавлен изохорно-изотермический потенциал (энергия Гельмгольца) F = U – TS. Поскольку большинство процессов в закрытых системах совершаются при постоянных Т и Р, то наиболее важны и используемы на практике соотношения для энергии Гиббса.
3.4. Основные термодинамические функции индивидуальных веществ Количество тепла, принимаемое молем вещества, при повышении его температуры на 1 градус, называется его мольной теплоемкостью, соответственно при постоянном объеме или при постоянном давлении
Непосредственное использование 1-го начала термодинамики в форме (3.2') показывает, что CV связана с изменением внутренней энергии. Дифференциал энтальпии Н = U + P·V при постоянном давлении (dH)Р = dU + P·dV = (δQ)Р сопоставленный с (3.2') показывает, что CР взаимосвязана с изменением энтальпии. Вытекающая из последнего соотношения взаимосвязь мольных теплоемкостей при постоянном давлении и постоянном объеме для газов (верхняя строка в (3.20)) легко устанавливается с использованием мольного уравнения Менделеева-Клапейрона.
Для твердых тел (нижняя строка) эта взаимосвязь выражается через молярный объем при 0 К (V0), изобарический коэффициент термического расширения (α) и изотермический коэффициент сжимаемости твердого тела (β). Энтальпия нагревания вещества при изменении температуры от Т1 до Т2 − результат интегрирования CР (3.19):
Температурное изменение энтропии при постоянном давлении следует из исходных определений энтропии (3.3) и теплоемкости CР:
На рисунке приведен результат калориметрических измерений теплоемкости (квадратики) циклогексена - исходной функции для расчета энтальпии (кружочки) и энтропии (треугольники). Термохимия (термодинамический раздел химии), кроме теплоемкости, занимается определением температур Tk и теплот При наличии такой информации основные (наиболее используемые) термодинамические функции рассчитываются по формулам
Дополненные стандартными энтальпиями образования (см. далее) они составляют основу термодинамических банков данных.
3.5. Термодинамические функции реакций Предваряя анализ тепловых эффектов химических реакций, ещё раз остановимся насимвольном уравнении химической реакции
Реагенты в уравнении реакции, естественно, со сменой знака перенесём в правую часть 0 = ν1 A1 + ν2 A2 + ν3 A3 + ν4 A4. (0 = −3H2 −N2 + 2NH3). Стехиометрические коэффициенты для реагентов при этом следует считать отрицательными: (ν1 = -ν'1, ν2 = - ν'2). Компактное и математически изящное уравнение химической реакции из произвольного числа компонентов принимает вид: 0 = Σνi Ai, νi < 0для реагентов. (3.25) Все текущие, в том числе и конечные количества реагентов и продуктов реакции единообразно выражаются через реакционную переменную ξ,: Δni = νi ξ ,ni = n0i + νi ξ . (3.26) Изменение числа молей при протекании реакции пропорционально стехиометрическому коэффициенту – закон кратных отношений. Если реакция происходит при постоянном объеме V, то указанный закон будет действовать и для концентраций (Ci = ni/(V, л)) − молярности). Разделив (3.26) на V получим ΔСi = νi ξ',Сi = С0i + νi ξ' , где ξ' = ξ/ V (3.26')
Закон сохранения массы для реакции (3.25) с использованием соотношений (3.26) 0 = ΣΔmi = Σ( MiΔni) = ξ Σ( Mi νi ) сводится к равной нулю стехиометрической сумме мольных масс Mi: Σ Mi νi = 0.
Реакции синтеза аммиака 3H2 + N2 = 2NH3 соответствует менее привычная для химиков (1) (2) (3) форма (3.25): 0 = −3H2 − N2 + 2NH3. Убывающим по реакции веществам соответствуют отрицательные стехиометрические коэффициенты, а прибывающим – положительные. В частности, исходному «стехиометрическому» составу n01 =3 моль, n02 =1 моль, n03 =0 моль при «полном, 100%-ном» завершении реакции соответствует ξ=1 моль(последняя строка нижеследующей таблички). Таблица. Три задачки 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 . (3.3)
. (3.3) . (3.3')
. (3.3') = 0), в которой протекают самопроизвольные, т.е. необратимые процессы, всегда наблюдается увеличение энтропии (ΔS > 0).
= 0), в которой протекают самопроизвольные, т.е. необратимые процессы, всегда наблюдается увеличение энтропии (ΔS > 0). . (3.4)
. (3.4) . (3.7)
. (3.7)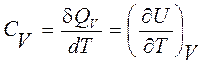 ,
,  . (3.19)
. (3.19) (3.20)
(3.20) . (3.21)
. (3.21) . (3.21')
. (3.21')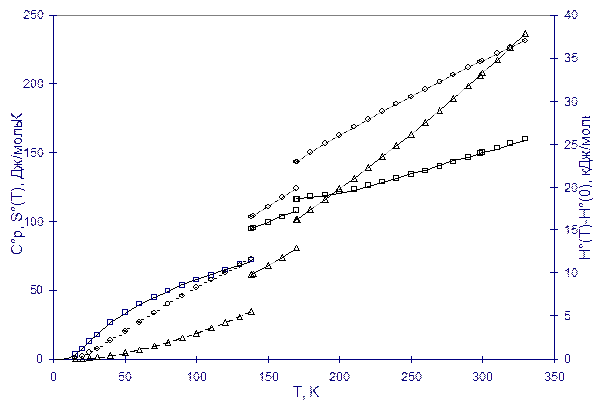
 фазовых и полиморфных превращений.
фазовых и полиморфных превращений. , (3.23)
, (3.23) . (3.24)
. (3.24)