
|
|
Транспортная задача и её решение методом потенциалов12
Постановка транспортной задачи: Транспортная задача является задачей линейного программирования. В общей постановке она выглядит следующим образом. Имеется m пунктов отправления (поставщиков) Требуется составить такой план перевозок, при котором весь груз из пунктов отправления был бы доставлен потребителям и при этом спрос потребителей был бы удовлетворён, а транспортные издержки были минимальными. Для разрешимости данной задачи необходимо и достаточно, чтобы сумма запасов была равна сумме потребностей всех пунктов, т.е. Для наглядности транспортную задачу удобно представлять в виде таблицы, которую называют распределительной.
В таблице количество груза, перевозимого от поставщика Матрица Матрица Общие суммарные затраты, связанные с перевозкой груза, можно представить в виде функции
Эта функция называется целевой функцией. Кроме этого, переменные должны удовлетворять ограничениям по потребностям, по запасам и условиям неотрицательности. Всё это с учётом целевой функции можно записать в виде:
Условия (2) образуют систему ограничений. Любой план, удовлетворяющий этой системе, называется допустимым. Таким образом, можно математически сформулировать транспортную задачу: Даны система ограничений и целевая функция. Требуется среди множества решений системы найти такой план перевозок, который минимизирует целевую функцию. Отыскание допустимого плана может осуществляться разными способами: Правило «северо-западного угла».Суть данного правила состоит в следующем. Таблица заполняется, начиная с левого верхнего угла (северо-западного), двигаясь по строке вправо или по столбцу вниз в направлении правого нижнего угла. Пример 1. Сельхозпредприятия
Требуется найти допустимый план задачи. Решение. Найдём допустимый план задачи с помощью правила «северо-западного угла».
Затраты на перевозку составят
Правило «минимального элемента».Допустимый план, построенный по правилу «северо-западного угла», обычно оказывается далёким от оптимального. Поэтому в дальнейшем потребуется достаточно много преобразований для достижения оптимального плана. Сократить число таких преобразований позволяет правило «минимального элемента». Суть этого правила в следующем. Заполнение таблицы начинается с клетки, которой соответствует наименьший элемент Пример 2. Решить предыдущий пример, используя правило «минимального элемента». Решение.
Затраты на перевозку составят
Допустимый план задачи, полученный методом «северо-западного угла» или методом «минимального элемента», будем называть первоначальным планом. Одним из методов, позволяющих на основании первоначального плана получить оптимальный план, является метод потенциалов. Суть его в следующем. После того, как найден первоначальный план перевозок, каждому поставщику
Для определения числовых значений потенциалов, одному из них нужно придать произвольное числовое значение, а остальные вычислить по равенству (3). Для проверки оптимальности плана просматриваются свободные клетки и для каждой из них вычисляется сумма потенциалов
Эти суммы называются косвенными тарифами. Затем для каждой свободной клетки вычисляются разности
которые называются оценками (характеристиками) свободных клеток. План будет оптимальным, если для каждой свободной клетки оценка есть величина неотрицательная, т.е. Таким образом, для решения транспортной задачи методом потенциалов необходимо:
Если все Пример 3. Проверить на оптимальность первоначальный план, полученный в предыдущем примере, при котором затраты на перевозку составили Решение. Вначале для каждой заполненной клетки построим систему потенциалов, удовлетворяющих (3).
Затем для каждой незаполненной клетки найдём косвенные тарифы
Так как
Загрузив клетку (2,3) и перераспределив перевозки, получим новый план.
Затраты на перевозки равны Полученный план снова проверим на оптимальность, для чего для незаполненных клеток построим новую систему потенциалов и найдём оценки.
Так как все оценки неотрицательны, то полученный план перевозок является оптимальным.
Транспортная задача с открытой моделью
Если суммарные запасы поставщиков не совпадают с суммарным спросом потребителей, т.е. Если Если же Пример 4. Решить транспортную задачу:
Решение. Так как запасы меньше потребностей, то введём фиктивного поставщика
Первоначальный план найдём методом минимального элемента.
Проверим полученный план на оптимальность.
Так как все оценки неотрицательны, то план перевозок оптимален. При этом стоимость перевозок равна
Задачи транспортного типа Многие задачи, которые по экономическому смыслу не являются транспортными, в математическом смысле подобны транспортным, так как описываются аналогичной моделью. Таким образом, для из решения можно использовать рассмотренные ранее методы. Во многих задачах транспортного типа целевая функция максимизируется. Поэтому при составлении первоначального плана в первую очередь имеет смысл заполнять клетки с более высокими тарифами. Если происходит переход от одного допустимого плана к другому, то выбор клетки, подлежащей заполнению, должен производиться не по отрицательной, а по положительной оценке. Оптимальным будет такой допустимый план, которому в таблице сопутствуют свободные клетки с неположительными оценками (все Пример 5. На четырёх ткацких станках с объёмом рабочего времени 200, 300, 250 и 400 станко-часов за один час можно изготовить соответственно 26, 20, 34 и 50 деталей трёх видов. Суммарная потребность в деталях каждого вида равна 18000, 8000 и 13700. Прибыль от реализации одной детали каждого вида при изготовлении её на каждом станке дана в матрице тарифов:
Требуется составить такую программу загрузки станков, чтобы общая прибыль от реализации готовой продукции была максимальной. Решение. На первом станке можно изготовить Так как общая суммарная потребность тоже равна 39700 деталей, то имеем закрытую модель задачи транспортного типа. Данную задачу можно решить методом потенциалов. Для этого запишем её в виде таблицы.
Первоначальный план найдём методом «минимального элемента».
Проверим первоначальный план на оптимальность.
Так как
Так как все оценки не положительны, то полученный план оптимален. Программу загрузки станков можно записать в виде матрицы
Прибыль от реализации продукции будет равна Транспортная задача в сетевой постановке Условия транспортной задачи могут быть заданы в виде схемы, на которой условно изображены поставщики, потребители и дороги, их соединяющие. При этом указаны запасы груза, потребности и тарифы на перевозку единицы груза. Такая постановка транспортной задачи называется сетевой, а заданная схема – транспортной сетью. Пункты поставщиков и потребителей обозначаются кружками и называются вершинамисети. Запасы груза записываются в кружках положительными числами, а потребности – отрицательными. Дороги, связывающие поставщиков и потребителей, обозначаются линиями и называются дугами сети.
Решение транспортной задачи в сетевой постановке начинается с построения допустимого плана, который будем называть опорным. При нахождении опорного плана на транспортной сети поставки груза из вершины в вершину будем обозначать стрелками и на каждой стрелке указывать величину поставки. Опорный план должен удовлетворять следующим требованиям:
План распределения груза на следующей схеме отвечает этим требованиям. Проверим этот план на оптимальность. Для этого вначале вычислим потенциалы вершин. Например, вершине I присвоим значение потенциала, равное 0, и запишем его в рамке. Для нахождения потенциалов остальных вершин будем придерживаться правила: если стрелка выходит из вершины i и входит в вершину j, то для определения потенциала вершины j к потенциалу вершины i прибавляется тариф
В рассматриваемом примере потенциал вершины III равен 2 (0+2), потенциал вершины V равен 6 (0+6), потенциал вершины II равен 1 (6-5) и потенциал вершины IV равен 4 (1+3). Теперь найдём характеристики Для данного примера
Для улучшения плана следует загрузить ту дугу без стрелки, которой соответствует отрицательная характеристика. Если же таких дуг несколько, то для загрузки выбирается та дуга, которая имеет наименьшую характеристику из отрицательных. К этой дуге дорисовывается стрелка штриховой линией, которая направлена от вершины с меньшим потенциалом к вершине с большим потенциалом. В данном примере стрелка направлена от вершины IV к вершине V, так как отрицательна характеристика для дуги, соединяющей вершины IV и V. Для определения величины поставки для «загружаемой дуги» рассматриваются все стрелки образовавшегося контура, которые имеют направление, противоположное направлению новой стрелки. Затем среди этих стрелок находится стрелка с наименьшей поставкой. Выбранная величина прибавляется ко всем поставкам в стрелках, имеющих то же направление, что и новая стрелка, и вычитается из поставок в стрелках, направление которых противоположно направлению новой стрелки. Поставки в стрелках, не входящих в контур, остаются неизменными. Стрелка с выбранной наименьшей поставкой ликвидируется.
Новый допустимый план исследуем на оптимальность. Для этого построим систему потенциалов, положив потенциал вершины IV равным, например, 10. Затем для дуг без стрелок вычислим характеристики: 
12 Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
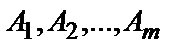 с запасами
с запасами 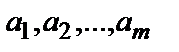 единиц груза. Имеется n пунктов назначения (потребителей)
единиц груза. Имеется n пунктов назначения (потребителей)  с потребностями
с потребностями  . Груз из пунктов отправления должен быть доставлен в пункты назначения. Известны транспортные издержки
. Груз из пунктов отправления должен быть доставлен в пункты назначения. Известны транспортные издержки  , связанные с перевозкой единицы груза из пункта
, связанные с перевозкой единицы груза из пункта  в пункт
в пункт  .
. . Транспортная задача, в которой выполнено это условие, называется закрытой (или транспортной задачей с закрытой моделью).
. Транспортная задача, в которой выполнено это условие, называется закрытой (или транспортной задачей с закрытой моделью).











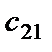








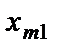









 к потребителю
к потребителю  обозначено через
обозначено через 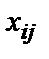 .
. называется матрицей тарифов, а числа
называется матрицей тарифов, а числа  – тарифами.
– тарифами. называется планом транспортной задачи. Здесь каждое число
называется планом транспортной задачи. Здесь каждое число  обозначает количество единиц груза, который надо доставить от i-го поставщика к j-му потребителю. Матрицу Х называют ещё матрицей перевозок.
обозначает количество единиц груза, который надо доставить от i-го поставщика к j-му потребителю. Матрицу Х называют ещё матрицей перевозок. .
.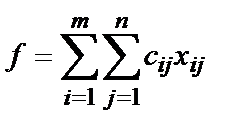
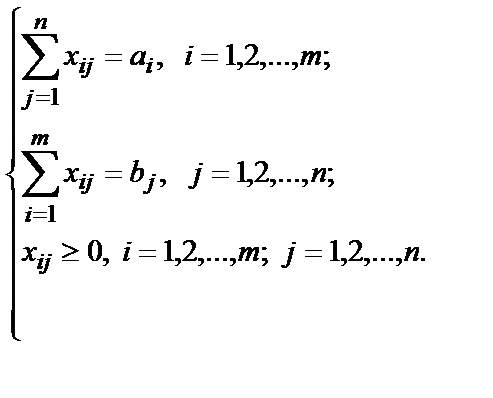
 ежедневно выделяют соответственно 30, 40 и 20 ц молока для снабжения пунктов
ежедневно выделяют соответственно 30, 40 и 20 ц молока для снабжения пунктов  . Стоимость перевозки и потребности пунктов даны в таблице.
. Стоимость перевозки и потребности пунктов даны в таблице.






 .
. из всей матрицы тарифов. Затем остаток по столбцу или строке помещается в клетку того же столбца или строки, которым соответствует следующее по величине значение
из всей матрицы тарифов. Затем остаток по столбцу или строке помещается в клетку того же столбца или строки, которым соответствует следующее по величине значение  и т.д.
и т.д. .
. (каждой строке) ставится в соответствие некоторое число
(каждой строке) ставится в соответствие некоторое число  , а каждому потребителю
, а каждому потребителю  (каждому столбцу) – некоторое число
(каждому столбцу) – некоторое число  . Числа
. Числа  и
и 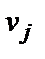 называются потенциалами поставщика и потребителя и выбираются так, чтобы в любой занятой (загруженной) клетке их сумма равнялась тарифу этой клетки, т.е.
называются потенциалами поставщика и потребителя и выбираются так, чтобы в любой занятой (загруженной) клетке их сумма равнялась тарифу этой клетки, т.е.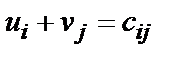 .
. .
. ,
, . Отрицательные оценки указывают на перспективность клеток, загрузка которых приведёт к улучшению плана.
. Отрицательные оценки указывают на перспективность клеток, загрузка которых приведёт к улучшению плана. построить какой-нибудь допустимый план перевозок (первоначальный план);
построить какой-нибудь допустимый план перевозок (первоначальный план); вычислить потенциалы
вычислить потенциалы  и
и  ;
; вычислить суммы потенциалов для свободных клеток (косвенные тарифы)
вычислить суммы потенциалов для свободных клеток (косвенные тарифы)  ;
; проверить оценки
проверить оценки  .
. для свободных клеток, то полученный план будет оптимальным. Если хотя бы одна оценка
для свободных клеток, то полученный план будет оптимальным. Если хотя бы одна оценка  , то в число занятых клеток вводят клетку, для которой оценка минимальна, и получают новый план перевозок. Процесс продолжается до тех пор, пока не будет получен план, для которого все
, то в число занятых клеток вводят клетку, для которой оценка минимальна, и получают новый план перевозок. Процесс продолжается до тех пор, пока не будет получен план, для которого все  .
. .
.





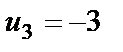
 и оценки
и оценки  :
: 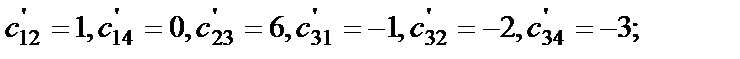
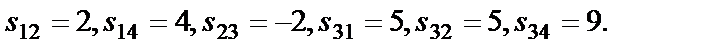
 , то клетка (2,3) является перспективной для перевозок и её необходимо загрузить.
, то клетка (2,3) является перспективной для перевозок и её необходимо загрузить.
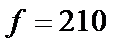 .
.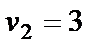


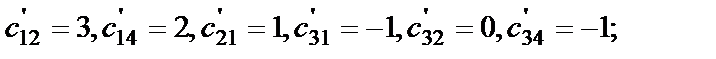
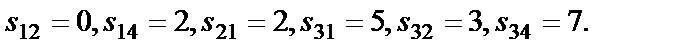
 , то такая транспортная задача называется транспортной задачей с открытой моделью.
, то такая транспортная задача называется транспортной задачей с открытой моделью. , то в математическую модель транспортной задачи вводится фиктивный (n+1)-й пункт потребления. В таблице появится столбец, для которого потребность равна разности между запасами поставщиков и фактическим спросом потребителей
, то в математическую модель транспортной задачи вводится фиктивный (n+1)-й пункт потребления. В таблице появится столбец, для которого потребность равна разности между запасами поставщиков и фактическим спросом потребителей  . Все тарифы на доставку груза потребителю
. Все тарифы на доставку груза потребителю  (фиктивному потребителю) считаются равными нулю. В этом случае задача становится транспортной задачей с закрытой моделью.
(фиктивному потребителю) считаются равными нулю. В этом случае задача становится транспортной задачей с закрытой моделью. , то вводится фиктивный (m+1) – й поставщик, для которого запас груза равен
, то вводится фиктивный (m+1) – й поставщик, для которого запас груза равен  . Тарифы на доставку груза от фиктивного поставщика
. Тарифы на доставку груза от фиктивного поставщика  полагают равными нулю. Это уже будет закрытая модель транспортной задачи.
полагают равными нулю. Это уже будет закрытая модель транспортной задачи. .
.








 . Из последней таблицы видно, что третьему потребителю не хватило 5 единиц груза.
. Из последней таблицы видно, что третьему потребителю не хватило 5 единиц груза. ).
).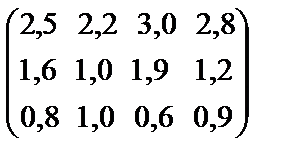 .
. деталей, на втором –
деталей, на втором –  , на третьем –
, на третьем –  и на четвёртом –
и на четвёртом –  деталей. Всего можно изготовить 39700 деталей.
деталей. Всего можно изготовить 39700 деталей.
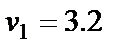






 ;
; .
. , то клетка (2,3) является перспективной и нужно перераспределить загрузку станков.
, то клетка (2,3) является перспективной и нужно перераспределить загрузку станков.

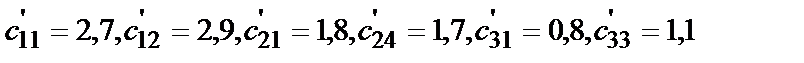 ;
; .
.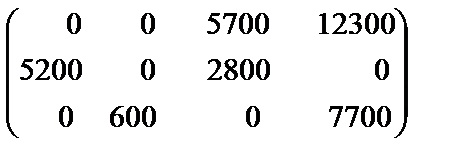
 .
. все запасы должны быть распределены, а потребности удовлетворены;
все запасы должны быть распределены, а потребности удовлетворены; к каждой вершине должна подходить или выходить из неё хотя бы одна стрелка;
к каждой вершине должна подходить или выходить из неё хотя бы одна стрелка; стрелки не должны образовывать замкнутый контур;
стрелки не должны образовывать замкнутый контур; общее количество стрелок должно быть на единицу меньше числа вершин.
общее количество стрелок должно быть на единицу меньше числа вершин.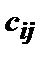 ; если же стрелка выходит из вершины j и входит в вершину i, то для определения потенциала вершины j из потенциала вершины i вычитается тариф
; если же стрелка выходит из вершины j и входит в вершину i, то для определения потенциала вершины j из потенциала вершины i вычитается тариф  .
. дуг без стрелок по правилу: из большего потенциала вычитается меньший, а затем эта разность вычитается из соответствующего тарифа. Если все характеристики получатся не отрицательными, то составленный план перевозок будет оптимальным. Если же среди характеристик есть отрицательные, то план перевозок не оптимален и его можно улучшить.
дуг без стрелок по правилу: из большего потенциала вычитается меньший, а затем эта разность вычитается из соответствующего тарифа. Если все характеристики получатся не отрицательными, то составленный план перевозок будет оптимальным. Если же среди характеристик есть отрицательные, то план перевозок не оптимален и его можно улучшить. ,
,  .
. ,
,  . Так как характеристики положительны, то полученный план перевозок является оптимальным. При этом значение целевой функции равно
. Так как характеристики положительны, то полученный план перевозок является оптимальным. При этом значение целевой функции равно  .
.