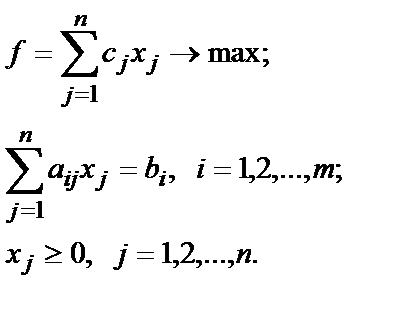|
|
Графический способ решения задач линейного программирования12 Элементы математического Программирования Основные понятия и задачи математического программирования
В практической деятельности специалист экономического профиля часто сталкивается с решением задач, которые характеризуются следующими свойствами:
Для решения таких задач разработаны методы, позволяющие находить наилучший вариант из всех возможных. Раздел математики, изучающий эти методы, называется математическим программированием. Для решения конкретной экономической задачи нужно прежде всего сформулировать её математически. Это означает, что нужно построить математическую модель экономической задачи, т.е. экономико-математическую модель. Построение такой модели распадается, как правило, на два этапа. На первом этапе цель задачи (прибыль, издержки производства и др.) представляется в виде некоторой зависимости от искомых величин. Полученное выражение называется целевой функцией или функционалом задачи. На втором этапе формулируются условия, которые должны быть наложены на искомые величины. Эти условия вытекают из наличия ресурсов, из условий технологии, различных экономических и технических факторов и т.д. Обычно такие условия записываются с помощью уравнений и неравенств. Эти условия называются системой ограничений данной задачи. Задача математического программирования формулируется следующим образом: найти такие значения неизвестных, которые удовлетворяли бы системе ограничений и доставляли целевой функции наибольшее или наименьшее значение (максимум или минимум). Совокупность численных значений неизвестных называется планом задачи. Любой план, удовлетворяющий системе ограничений, называется допустимым планом. Допустимый план, доставляющий целевой функции максимум или минимум, называется оптимальным(наилучшим) планом. Таким образом, решение задачи математического программирования заключается в том, чтобы из всего множества допустимых планов выбрать оптимальный. Следует отметить, что в реальных экономических задачах число переменных бывает обычно очень большим. Поэтому практическая реализация алгоритмов решения таких задач невозможна без использования современной вычислительной техники. Если целевая функция и система ограничений линейны, т.е. переменные входят в них в первой степени, то математическое программирование называется линейным. Методы линейного программирования применяются к таким задачам, в которых:
Основная задача линейного программирования формулируется следующим образом: Пусть задана линейная целевая функция
и система ограничений
Требуется найти такие значения неизвестных В системе ограничений вместо знаков Рассмотрим типичные задачи линейного программирования: транспортную задачу; задачу об использовании ресурсов; задачу оптимального сочетания посевных площадей; задачу составления суточного рациона. Транспортная задача (пример реализации в Ехcel). В городе имеется два склада муки и два хлебозавода. Ежедневно с первого склада вывозится 50 т муки, а со второго – 70 т. Эта мука доставляется на хлебозаводы, причём первый хлебозавод получает 40 т муки, а второй – 80 т. Перевозка одной тонны муки с первого склада на первый хлебозавод стоит 12 тыс. руб., с первого склада на второй хлебозавод – 16 тыс. руб., со второго склада на первый хлебозавод – 8 тыс. руб., со второго склада на второй хлебозавод – 10 тыс. руб. Требуется спланировать перевозки таким образом, чтобы их стоимость была минимальной. Решение. Обозначим:
По условию задачи построим систему ограничений:
Целью задачи является минимизация общей стоимости перевозок:
С математической точки зрения решение задачи состоит в том, чтобы найти такие числа Из четырёх уравнений системы (3) четвёртое является следствием первых трёх (1+2–3). Поэтому будем рассматривать только первые три уравнения
Из системы (5) получим:
Так как по условию задачи все
Таким образом, задавая любое значение Следовательно, Таким образом, оптимальный план перевозок имеет вид:
Задача об использовании ресурсов (пример реализации в Ехcel). Задача 1. Мебельная фабрика выпускает стулья двух типов. На изготовление одного стула первого типа стоимостью 360 тыс. руб. расходуется 2 м досок, 0.5 Решение. Обозначим:
Запишем ограничения по доскам, по ткани и по времени:
Целевая функция имеет вид:
Задача 2. На участках различного плодородия площадью 100 га и 200 га нужно посеять пшеницу и кукурузу. Урожайность пшеницы на первом участке 20 ц/га, на втором – 25 ц/га. Урожайность кукурузы на первом участке 35 ц/га, на втором – 30 ц/га. По плану должно быть собрано не менее 1500 ц пшеницы и 4500 ц кукурузы. Цена 1 ц пшеницы 18 у.е., кукурузы – 14 у.е. Необходимо распределить посевы пшеницы и кукурузы таким образом, чтобы получить максимум валовой продукции в денежном выражении, если участки используются полностью. Составить экономико-математическую модель. Решение. Обозначим:
Запишем целевую функцию и систему ограничений:
Составление суточного рациона (пример реализации в Ехcel). При составлении суточного рациона кормления скота можно использовать свежее сено (не более 50 кг) и силос (не более 85 кг). Рацион должен содержать не менее: 30 к.е., 1 кг белка, 100 г кальция и 80 г фосфора. Необходимые данные приведены в таблице.
Требуется составить рацион таким образом, чтобы себестоимость его была наименьшей. Построить экономико-математическую модель. Решение. Обозначим:
Составим систему ограничений и целевую функцию:
Графический способ решения задач линейного программирования Графический способ целесообразно использовать для решения задач с двумя переменными. Использование этого способа рассмотрим на примере. Пример. Пусть дана система ограничений и целевая функция:
Построить область допустимых решений и найти максимум целевой функции. Графический метод решения задачи линейного программирования применим к узкому классу задач и с его помощью эффективно можно решать задачи, содержащие не более двух переменных. Одним из универсальных методов решения задач линейного программирования является симплексный метод (симплекс-метод). Пусть задача записана в виде:
Если данная задача разрешима, то её оптимальный план совпадает с одним из допустимых планов системы уравнений. Именно этот план и отыскивается симплекс-методом в результате упорядоченного перебора допустимых планов. Упорядоченность понимается в том смысле, что при переходе от одного допустимого плана к другому соответствующие им значения целевой функции возрастают (не убывают). Поэтому симплекс-метод называется методом последовательного улучшения плана. Так как общее число допустимых планов конечно, то через конечное число шагов либо будет найден оптимальный план, либо будет установлена неразрешимость задачи. Таким образом, решение задачи складывается из двух этапов: на первом этапе находят какой-либо начальный допустимый план; на втором этапе по специальным правилам переходят от начального допустимого плана к другому, более оптимальному, затем к следующему и так до тех пор, пока задача не будет решена.

12 Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 на искомые величины накладывается большое число ограничительных условий;
на искомые величины накладывается большое число ограничительных условий; задача имеет бесчисленное множество решений, из которых надо выбрать наилучшее.
задача имеет бесчисленное множество решений, из которых надо выбрать наилучшее.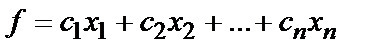
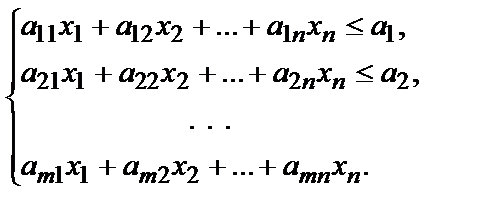
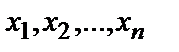 , которые удовлетворяли бы системе ограничений и доставляли целевой функции максимум или минимум.
, которые удовлетворяли бы системе ограничений и доставляли целевой функции максимум или минимум.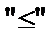 могут быть
могут быть  или
или  .
. – количество муки (т), перевозимой с первого склада на первый хлебозавод;
– количество муки (т), перевозимой с первого склада на первый хлебозавод; – количество муки (т), перевозимой с первого склада на второй хлебозавод;
– количество муки (т), перевозимой с первого склада на второй хлебозавод; – количество муки (т), перевозимой со второго склада на первый хлебозавод;
– количество муки (т), перевозимой со второго склада на первый хлебозавод; – количество муки (т), перевозимой со второго склада на второй хлебозавод.
– количество муки (т), перевозимой со второго склада на второй хлебозавод. (3)
(3) (4)
(4) , которые удовлетворяли бы системе ограничений (3) и минимизировали стоимость перевозок (4).
, которые удовлетворяли бы системе ограничений (3) и минимизировали стоимость перевозок (4). (5)
(5)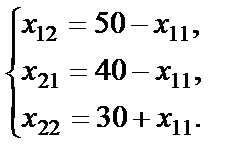 (6)
(6) , то
, то или
или  т.е.
т.е.  (7)
(7) , удовлетворяющее соотношению (7), можно получать любые из возможных планов перевозок. При этом стоимость перевозок будет в каждом случае различной. По условию задачи нужно найти минимальную стоимость. Подставим (6) в (4) и получим
, удовлетворяющее соотношению (7), можно получать любые из возможных планов перевозок. При этом стоимость перевозок будет в каждом случае различной. По условию задачи нужно найти минимальную стоимость. Подставим (6) в (4) и получим  . Значение этой функции будет минимальным при наибольшем значении
. Значение этой функции будет минимальным при наибольшем значении  из промежутка (7).
из промежутка (7).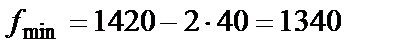 при
при  . Значения остальных переменных определяются по формулам (6):
. Значения остальных переменных определяются по формулам (6): 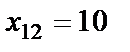 ,
,  ,
, 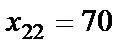 .
.
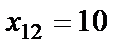 ,
, 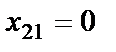 ,
, 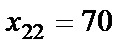 ,
,  . При любом другом допустимом плане перевозок стоимость перевозок окажется выше.
. При любом другом допустимом плане перевозок стоимость перевозок окажется выше. обивочной ткани и 2 чел./ч рабочего времени. Для стульев второго типа эти данные составляют: 460 тыс. руб.; 4 м; 0.25
обивочной ткани и 2 чел./ч рабочего времени. Для стульев второго типа эти данные составляют: 460 тыс. руб.; 4 м; 0.25  и 2.5 чел./ч. В распоряжении фабрики имеется 440 м досок, 65
и 2.5 чел./ч. В распоряжении фабрики имеется 440 м досок, 65 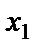 – количество стульев первого типа;
– количество стульев первого типа;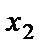 – количество стульев второго типа.
– количество стульев второго типа.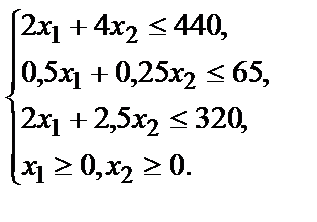
 .
. – площадь под пшеницу на первом участке;
– площадь под пшеницу на первом участке; – площадь под пшеницу на втором участке;
– площадь под пшеницу на втором участке;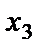 – площадь под кукурузу на первом участке;
– площадь под кукурузу на первом участке;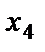 – площадь под кукурузу на втором участке.
– площадь под кукурузу на втором участке.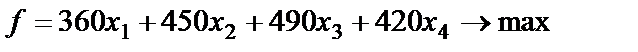
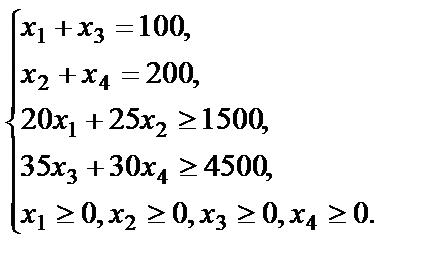
 – количество сена (кг) в рационе;
– количество сена (кг) в рационе;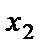 – количество силоса (кг) в рационе.
– количество силоса (кг) в рационе.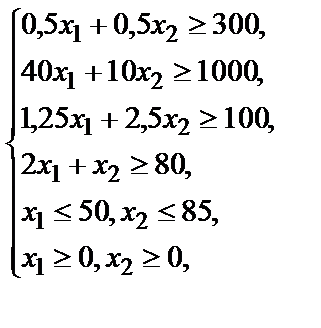
 .
.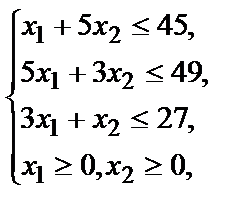
 .
.