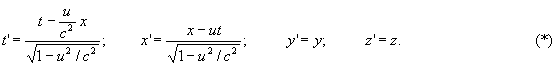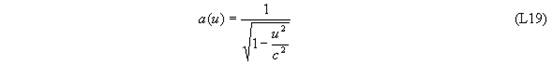|
|
Вывод преобразований Лоренца из принципа относительностиСодержание 1. Постоянство скорости света — следствие преобразований Лоренца 2. Вывод преобразований Лоренца из принципа относительности 3. Вывод преобразований Лоренца в трехмерном векторном виде 4. Следствия из преобразований Лоренца 5. Преобразования Лоренца-Фока (лекция для студентов) 6. Примечания: o О линейности преобразований Лоренца o О преобразовании поперечных размеров движущихся тел o Вывод явного вида функции a(u) Литература Постоянство скорости света - следствие преобразований Лоренца В основе теории относительности лежит известный и в ньютоновской механике принцип равноправия инерциальных систем отсчета. Этот принцип был распространен на все физические явления, включая электромагнитные. Новым в релятивистской физике стал постулат постоянства скорости света в вакууме c во всех инерциальных системах отсчета и ее независимость от скоростей источника и приемника излучения. Этот постулат противоречит классическому закону сложения скоростей. Наблюдатель в одной инерциальной системе отсчета описывает событие, произошедшее в точке с координатами x, y, z в момент времени t. В другой инерциальной системе, движущейся со скоростью u вдоль оси X относительно первой, это же событие наблюдается в точке с координатами x’, y’, z’ в момент времени t’. Связь этих координат и моментов времени определяется преобразованиями Лоренца:
Вывод преобразований Лоренца из принципа относительности Приведем вывод этих преобразований, основанный только на принципе относительности (т. е. на равноправии всех инерциальных систем отсчета). В этом выводе постулат постоянства скорости света не используется ad hoc, а оказывается следствием принципа относительности. Обозначим множество всех инерциальных систем отсчета K. Рассмотрим две инерциальные системы отсчета k, k' из K, движущиеся друг относительно друга со скоростью u. Выберем декартовы координаты в этих системах отсчета так, чтобы в начальный момент времени начала коор инат совпадали, а оси были параллельны. В системе отсчета k моменты времени и координаты вдоль направления u будем обозначать t и x соответственно, в системе отсчета k' — t' и x' . Оси X и X' направим так, чтобы система k' двигалась со скоростью u относительно системы k вдоль оси X, а система k двигалась со скоростью -u вдоль оси X' системы k' .
а в системе k' — уравнением
Преобразование координат t, x, y, z системы k в координаты t', x', y', z' системы k' должно быть таким, чтобы уравнение (L1) переходило в уравнение (L2). Это означает, что прямая в пространстве r, t должна переходить в прямую в пространстве r', t'.
где величины aij зависят только от скорости относительного движения систем отсчета.
Действительно, в силу однородности и изотропности нашего пространства, преобразования вдоль оси X не должны зависеть от значения координат y и z. Сами координаты y и z тоже не должны преобразовываться, иначе поперечные размеры тел будут зависеть от скорости их движения, что приведет к неравноправию различных инерциальных систем отсчета. (см. примечание 2) (Для тех, кого эти соображения не убедили, здесь приведен вывод преобразований Лоренца в трехмерной векторной форме) Найдем явный вид четырех неизвестных функций att(u), atx(u), axt(u), axx(u), опираясь только на принцип относительности и с войства однородности и изотропности нашего пространства-времени. Повернем оси координат в двух системах отсчета вокруг некоторого направления, перпендикулярного скорости u, на 1800. Это приведет замене x на -x и x' на -x '. Если теперь заменить направление скорости u на противоположное, т. е. на -u, то преобразования (L3), (L4) примут вид
Заметим, что произведенные преобразования привели к тому, что система k' движется, как и прежде, вдоль оси X системы k со скоростью u. В силу изотропности нашего пространства (равноправия всех направлений) вид равенств (L3), (L4) не зависит от направления осей X, X' следовательно формулы (L6), (L7) должны совпадать с (L3), (L4). Это возможно, если функции att(u), axx(u) - четные, а функции axt(u), atx(u) — нечетные. Из уравнений (L3), (L4) следует axt(u)= vuatt(u). Аналогично точка x'=0 движется со скоростью u вдоль оси X в системе k: x=ut. Из тех же уравнений следует axt(u)= -uaxx(u) или a xx(u)= att(u)?a(u). Вводя для симметрии вместо нечетной функции atx(u) четную функцию g(u) по формуле atx(u)= -ua(u)g(u), получаем
Рассмотрим еще одну инерциальную систему отсчета k'', движущуюся со скоростью u ' вдоль о си X' системы k'. Закон преобразования из системы k' в систему k'' должен иметь вид, аналогичный (L8), (L9):
Подставляя в (L10), (L11) выражения для x', t' из (L8), (L9), получаем
С другой стороны, равенства (L12), (L13) описывают переход из системы k в систему k' , движущуюся вдоль оси X с некоторой скоростью u'':
Из сравнения соотношений (L12), (L13) с (L14), (L15) следуют равенства
Равенство (L16) вводит некоторую постоянную величину, размерность которой — обратный квадрат скорости. Эта величина одинакова в о всех системах отсчета, и ее численное значение не может быть выведено из каких-либо общих принципов. Экспериментальное значение этой величины g=c-2 , где c — скорость света в вакууме. В классической нерелятивистской механике g=0. Равенство (L17) — функциональное уравнение, из которого (с учетом (L18)) можно определить вид неизвестной функции a(u) (см. примечание 3):
Равенство (L18) определяет закон сложения скоростей для движений вдоль оси X: Важное свойство этого закона: Следовательно, если скорость частицы (или электромагнитной волны) равна c в одной системе отсчета, то она одинакова во всех инерциальных системах отсчета. Итак, мы вывели соотношения (*) из принципа относительности и получили следствием постоянство скорости c во всех инерциальных системах отсчета. Важно отметить принципиальное отличие данного подхода к выводу преобразований Лоренца от общепринятого. Постоянство скорости света во всех инерциальных системах отсчета — это экспериментальный факт, установленный с определенной степенью точности. Приведенный выше вывод не опирается на этот факт, из него следует только существование скорости, одинаковой во всех инерциальных системах отсчета. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|