
|
|
Моделирование технологий производств издержек и спроса12 …………………….. Q= f (k,l) = > …………….. ………………………………………. Замечание. Предельный продукт фактора произв-ва это ф-я, …….. От кол-ва труда и капитала задействованного в процессе производства. Lim MPL (LK) = + ¥ Определения: про взаимосвязь м/у факторами произв-ва. 1. Труд и капитал являются поддерживающими (взаимодополняемыми) факторами в процессе произв-ва, если с увеличением включенности в произв-во одного фактора растет предельный продукт другого фактора.
2. Труд и капитал являются замещающими (взаимозамещающими) факторами в процессе произв-ва, если с увеличением включенности в произв-во одного фактора предельный продукт другого фактора уменьшится.
Определение. Про зависимость м/у кол-ом произведенной продукции и ростом объемов использования факторов. ] l > 1 -произвольное число, тогда технология произв-ва Q=f(L,K) соответствует : Т.е при росте вовлеченности в процессе произв-ва труда и капитала в l раз выход продукции увеличивается более чем в l раз. 3. постоянная отдача от масштаба (ПОМ) f (lk, ll) =lf (k,l) Функция издержек Функция издержек(TC(total costs)) Функция издержек отражает зависимость общих производственных затрат от цен использования факторов производства и объемов производства. W – з/п; R – размер ставки(проценты) Тогда для полных издержек Функция средних издержек (average cost)
Функция предельных издержек
Теорема Если минимум функции средних издержек допускается при строго положительном значении выпуска, то для этого определенного уровня выпуска средние издержки равный предельным издержкам. То есть если Доказательство Рассмотрим производственную функцию
3 случая: 1)  –уменьшающаяся отдача от масштаба; 2) –уменьшающаяся отдача от масштаба; 2) 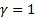 ;-постоянная о.м. 3) ;-постоянная о.м. 3) 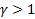 – возрастающая о.м. – возрастающая о.м.Частные производные 1) W – размер з/п
 если если  ; если ; если  ; если ; если 
 ; ;  ; ; 
Функция спроса Функция спроса Q(p), p – цена ед. товара. Обратная функция спроса - P(Q).
Функция эластичности Функция эластичности Эластичность показывает как изменится спрос с любым небольшим относительным изменением цены. Обозначается Определение Для данного Q спрос называется: 1) эластичным,
Производитель получается Total revenue
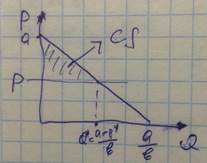
Теорема Если функция строга линейна, то функция предельного дохода также линейна, имеет ту же точку пересечения с осью ординат, но ее наклон относительно этой оси меньше в 2 раза, чем у кривой спроса. Доказательство Теорема Доказательство Потребительский излишек(CS – consumer surplus)
-Это мера благосостояния, характеризующая выигрыши благосостояния товара при открытии рынка товара. Чтобы его посчитать, необходимо найти площадь заштрихованного треугольника на рисунке.
20. Рыночные структуры Совершенная конкуренция Покупатель или продавец называется конкурирующим, а его поведения называется совершенно конкуреynysv, если он предполагает или считает, что рыночная цена является заданной и что его действия не могут на нее повлиять. Кооперативные игры N={1,2,3,…,n} Кооперативная игра – отображение множества из множества всех подмножеств?! V: 2N->R, V(ᴓ)=0 V[S] ∊R – способ множества (коалиции) зарабатывать V∊ Ядро – множество данных Х=(х1,х2,…,хn) ∊ RN таких, что Ядро – выпуклый многогранник в множестве RN Вектор Шепли (Sh) n! – возможность посмотреть n человек по одному и дополнительно друг к другу Sh= Возможны следующие случаи: 1) Ядро м.б пустым (находим вектор Шепли 2) ядро м.б не пустым и вектор Sh∊ ядру (находится внутри ядра) «хорошая игра» 3) ядро м.б не пустым, но вектор Шепли находится не в ядре «плохая игра» Супермодулярные кооперативные игры Sh=(ϕ1(ν), ϕ2(ν), …, ϕn(ν)) ϕi(ν)= k=|S|- размер коалиции (V(S)-V(S){i}) – вклад i-го игрока в коалицию Вектор Шепли – единственный делёж, который: a) симметричен ϕi(ν)= ϕj(ν) – для симметричных игр. Определение: 2 игрока симметричны, если присоединение любого из игроков к коалиции S одинаково усилит эту коалицию ∀ S b) аддитивен, т.е для 2х игр G= <N,ν> и G=<N,ω> и ∀i∊N справедливо равенство ϕj(ν+ ω)= ϕi(v)+ ϕ(ω) c) назначает ϕi(ν)=0 нулевым игрока i∊N (назначает нулевой выигрыш нулевым игрокам) Кооперативные игры Определение: Игрок нулевой, если его присоединение к коалиции дает нулевой выигрыш i – нулевой, если ν (S˽i)= ν (S) ∀S∊N Определение: Следующие 2 свойства 1) Для ∀ игрока i∊N, ∀T Игроки приносят больший выигрыш при подключении к большей коалиции 2) ∀ S,T Игра, обладающая 1 и 2 свойствами называется супермодулярной Теорема о CMD ⊐v – SMD=>∀ упорядочивания игроков σ∊Sn – дележ Шепли для упорядочивания σ ∊ ядру Следствие Эти дележи порождают ядро => ядро игры является выпуклой n! этих дележей

12 Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 > 0
> 0  > 0
> 0 измеряет общие издержки при производстве Q единиц товара при данных ценах на факторы производства(цена на рабочую силу W и капитал R)
измеряет общие издержки при производстве Q единиц товара при данных ценах на факторы производства(цена на рабочую силу W и капитал R)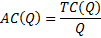
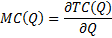
 и
и  , то
, то 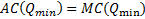
 ;
;  ;
; 
 ч.т.д.
ч.т.д. 
 ;
;  ;
;  ;
; 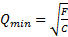
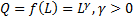



 >0 => возрастающая 2)
>0 => возрастающая 2) 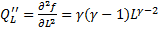
 ;
;  ;
;  >0;
>0;






 =>
=>  ,
, 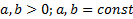
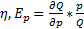
 ; 2)неэластичным,
; 2)неэластичным,  ; 3)единичная эластичность
; 3)единичная эластичность 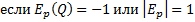

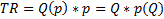
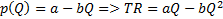

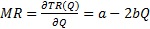 – функция предельного дохода
– функция предельного дохода
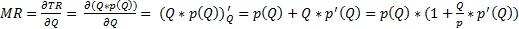
 ;
;  ;
; 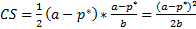

 – вектор из кол-ва чисел 2N, при котором одно из них равно 0
– вектор из кол-ва чисел 2N, при котором одно из них равно 0 , а также для ∀ S
, а также для ∀ S  N
N 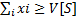
 < ∑ дележей>
< ∑ дележей>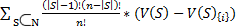
 (вектор v длинной 2N из действительных чисел) эквивалентны
(вектор v длинной 2N из действительных чисел) эквивалентны