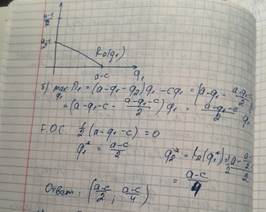|
|
Динамические игры с совершенной информацией12 Теория игр Существует несколько типов игр в экономике Статические с полной информацией Динамические с полной информацией Статические с неполной информацией Динамические с неполной информацией Игры с полной информацией Игроки принимают решения (делают выбор стратегии) независимо друг от друга и одновременно. Функции выигрышей всех игроков известны (всем игрокам). Игру можно представить в нормальной и экстенсивной форме. Нормальная форма игры определяет игроков, стратегии доступные любому игроку, выигрыши каждого игрока для каждой комбинации стратегий, которая может быть выбрана всеми игроками. Пусть в игре участвует n игроков, Si – множество всех стратегий доступных i-му игроку. si ∈Si – элемент множества стратегий, (s1, s2, …, sn) – комбинация стратегий, Ui (s1, s2, …, sn) – функция выигрыша игрока i. Нормальная форма игры с n игроками определяет множество стратегий всех игроков S1, S2, …, Sn и функции выигрыша для каждого игрока U1, U2, …, Un. G = {S1, S2, …, Sn, U1, U2, …, Un} Рассмотрим игру с n игроками в нормальной форме. Пусть si’, si’’ ∈ Si – достижимые стратегии для игрока i. Стратегия si’ строго доминируется стратегией si’’ если, для любых комбинаций стратегий других игроков, выигрыш игрока i, если он играет стратегию si’, строго меньше, чем если бы он играл стратегию si’’. Ui(s1, s2, …, si-1, si’, si+1, …, sn) < Ui(s1, s2, …, si-1, si’’, si+1, …, sn) Для любых (s1, s2, …, si-1, si+1, …, sn) Дилемма заключенного
Равновесие Нэша Рассмотрим игру в нормальной форме G = {S1, S2, …, Sn, U1, U2, …, Un} Стратегии (s1*, s2*, … , sn*) образуют равновесия Нэша, если для любого игрока i, стратегия si*это наилучший ответ игрока i (обозначается best response) на стратегии (s1*, s2*, …, si-1*, si+1*, …, sn*) остальных (n-1) игроков. Ui(si*, s-i*) ≥ Ui(si, s-i*) для любой достижимой стратегии si игрока i. Т.е. решение оптимизационной задачи
Утверждение 1. Рассмотрим игру для n игроков в нормальной форме. Представим, что в игре путем исключения доминируемых стратегий, мы исключили все стратегии кроме (s1*, s2*, … , sn*). Тогда эти стратегии являются единственным равновесием Нэша в данной игре. Утверждение 2. Рассмотрим игру в нормальной форме с n игроками. Если стратегии (s1*, s2*, … , sn*) являются равновесием Нэша, то они «выживут» при исключении доминируемых стратегий (но решения таким путем может и не существовать). Дуополия курно i=1,2. Q=q1+q2 (объем) P(Q)=a-Q (цена) ci(qi)=cqi (общие издержки фирмы i на продукцию Предельные издержки постоянны (чем больше производим, тем больше нам требуется). Нормальная форма игры. Стратегия Si = [0;+∞) выпустить продукцию от 0 до +∞. Ui=Пi. G = { Si = [0;+∞), Ui=Пi} i=1,2.
Si=qi (стратегия это то количество продукции, которое нужно произвести) Для любого i
У нас Решаем максимизационную задачу
Для 1 фирмы
Для 2 фирмы
Парламентское голосование Парламент разделен на три фракции (б. з. к.). Каждая из фракций может проголосовать за или против. G=<I={б,з,к}, Si={за, против}, Ui> Решение принимаются большинством голосов. Б – не хотят законопроект. З, К хотят законопроект. Если закон пройдет, то з,к получат 1, если не пройдет, то все получат 0. Б. За
Против
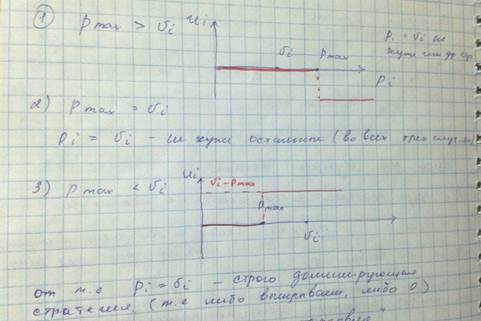
U1(За)=(-1,-1,-1,0) U1(Против)=(-1,0,0,0) U1(Против) доминирует U1(За). Смотрим стратегию против. Видим. Что равновесия Нэша это стратегия (против, за, за). 7. Аукцион Викри Некий предмет продается на аукционе. I=1..K+1 участник (Kигроков назвали такую же цену и сам участник). Цена по заявке pi. Побеждает участник, предложивший самую высокую цену по порядку убывания. Если i участок окажется победителем, то его выигрыш составит vi-pi , где vi ценность для него данного предмета. Выигрыш всех остальных 0. Pi=vi – доминирующая «правдивая» стратегия.
Pmax=max{p-i} – максимальная из всех цен, названных остальными.
Трагедия общин · N фермеров в деревне · Каждое лето все пасут своих коз на общих пастбищах · gi – количество коз i фермера. · G = g1 + g2 + … + gn · C – издержки на содержание козы · V(G) – ценность того, что одна коза пасется на пастбище с остальными козами · Существует Gmax – максимальное количество коз, которые пасутся на пастбище
· Идея: когда на пастбище мало коз, то выпас еще одной дополнительной козы мало повредит остальным, но когда коз итак много, то дополнительная коза сильно вредит. · Весной все фермеры решают сколько коз им содержать · Козы бесконечно делимы (функция непрерывна) · Стратегия фермера : выбрать gi ∈ G · Выигрыш фермера i:
Если
FOC N уравнений для каждого фермера. Складываем все эти уравнения.
Общественный оптимум (G**).
FOC v(G**) + G**v’(G**) - c=0 (2) Сравнивая (1) и (2) получаем G* > G **. Если фермер принимает во внимание только свой личный выигрыш, то общественное благо перерасходуется. Теорема Нэша Равновесие Нэша в смешанных стратегиях
a<b a<c DSNE в чистых стратегиях MSNE в смешанных стратегиях Определение Рассмотрим игру в нормальной форме G=<I; S1; Sn; u1 ….,Un> и предположим что si={si1,…Sik} тогда назовем смешанной стратегией игрока i-распределение вероятностей pi =(pi1…pik),где 0<=pik<=1 k=1..k pik Замечание о строго доминируемых и смешанных стратегиях Если Si строго доминируема,у I игрока не существует таких вероятностей >0 , чтобы было оптимально играть стратегию . Теорема Нэша 1950 Равновесие N в смешанных стратегиях существуют в любой конечной игре. Если n –конечное число игроков ,а также Si- множество стратегий с конечным числом элементов, то равновесие по Нэшу существует (возможно в смешанных стратегиях). Утверждение (характеристика равновесия по Нэшу в смешанных стратегиях для конечной игры) Смешанная стратегия p* является равновесной по Нэшу тогда и только тогда ,когда для каждого игрока I: 1)ожидаемый выйгрыш (для фиксированных pi* )для всех стратегий которым pi* приписывает положительные вероятности одинаковые 2)ожидаемы выйгрыш для каждой стратегии которой Pi* приписывает положитительные вероятности больше ожидаемого выигрышу любой стратегии .которой приписывает нулевые вероятности. Динамические игры с совершенной информацией Динамические игры с совершенной информацией Динамические игры с полной информацией игроки знают функции выигрыша друг друга на каждом ходу каждый игрок знает всю историю игры до этого хода. 1)игрок 1 выбирает действие A1 из набора допстимых действий 2)игрок 2 наблюдает A1 и выбирает действие A2 из доступного ему набора действия 3)игрок 3 получает выйгрыш u1 (a1, a2) и u2 (a1, a2). Метод стратной индукции индукции А)игрок 2 на 2ом шаге (зная А1)имеет единственное решение R2(a1)-функция наилучшего ответа 2ого игрока на ход первого.
Дуополия штакельберга

12 Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
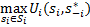
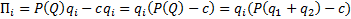
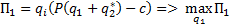
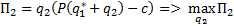
 будет равновесием Нэша, тогда и только тогда, когда
будет равновесием Нэша, тогда и только тогда, когда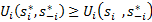 т.е.
т.е. 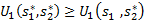 и
и 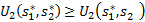
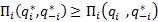
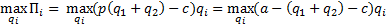
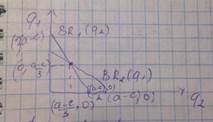
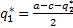 BR1(q2)
BR1(q2)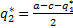 BR2(q1)
BR2(q1)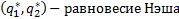
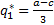
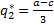
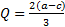
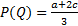
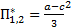
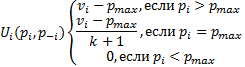
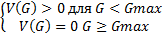
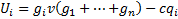
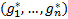 – равновесие Нэша, то для любого i, gi должно давать максимальный выигрыш при условии, что все остальные выбрали g-i*. Решаем задачу максимизации.
– равновесие Нэша, то для любого i, gi должно давать максимальный выигрыш при условии, что все остальные выбрали g-i*. Решаем задачу максимизации.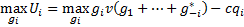
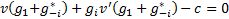
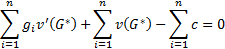
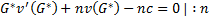
 равновесие Нэша для одного фермера. (1)
равновесие Нэша для одного фермера. (1)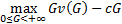
 Б)игрок 1 тоже может решить тоесть они знают что предпримет игрок 2.
Б)игрок 1 тоже может решить тоесть они знают что предпримет игрок 2.