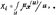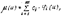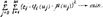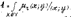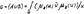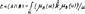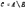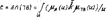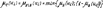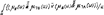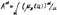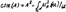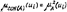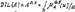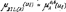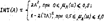|
|
Исчисление предикатов. Сколемовская стандартная форма формулы.Наличие разноимённых кванторов усложняет анализ суждений. Поэтому можно рассмотреть более узкий класс формул, содержащий только кванторы общности, т. е. F = "x1"x2…"xn(M) Для устранения кванторов существования разработан алгоритм Сколема, вводящий сколемовскую функцию для связи предметной переменной квантора существования с другими предметными переменными. Алгоритм Сколема: 1) представить формулу F в виде ПНФ; 2) найти наименьший индекс i квантора существования такой, что все предшествующие в префиксе кванторы есть кванторы общности: a) если i = 1, т. е. квантор $xi находится на первом месте префикса, то вместо переменной, связанной квантором существования, подставить всюду предметную постоянную ai, отличную от встречающихся предметных постоянных в матрице формулы, а квантор существования вычеркнуть в префиксе; b) если i > 1, т. е. квантор $xi находится не на первом месте префикса, а перед квантором существования стоит часть префикса, состоящая только из кванторов общности, то выбрать (i – 1)-местный функциональный символ, отличный от функциональных символов матрицы M и выполнить замену предметной переменной xi, связанной квантором существования на функцию f(x1; x2; … xn) и квантор существования вычеркнуть в префиксе; c) найти следующий индекс квантора существования и перейти к исполнению шага 2. Если таких индексов нет, то конец. Бескванторную часть формулы теперь можно преобразовать а виду КНФ или ДНФ. Чаще всего требуется выполнить преобразование к виду КНФ для логического вывода по принципу резолюции. Формулу, полученную в результате введения сколемовской функции и преобразованную в КНФ, т. е. F = "x1"x2…"xn(D1 & D2 & …), называют сколемовской стандартной формой формулы. В этой формуле Di – дизъюнкты, xi – предметные переменные. Каждый член дизъюнкта называют литерой. 17. Исчисление предикатов. Основные аксиомы вывода. Среди множества тождественно истинных формул существует подмножество, являющееся аксиомами исчисления предикатов, облегчающие процесс эквивалентных преобразований в процессе логического вывода. Ниже приведён набор наиболее распространённых аксиом (правил) для исчисления предикатов: 1) правило обобщения (или введения квантора общности): “если F1(t) ® F2(x) – выводимая формула и F1(t) не содержит свободной переменной x, то F1(t) ® "x(F2(x)) также выводима” __(F1(t) ® F2(x))__ (F1(t) ® "x(F2(x))) 2) правило удаления квантора общности: “если каждая предметная переменная входит в предикат F(x), то можно ввести терм t, свободный от предметной переменной x, но удовлетворяющий требованиям предиката F(t)” "x(F(x)) F(t) 3) правило конкретизации: “если F1(x) ® F2(t) выводимая формула и F2(t) не содержит свободных вхождений x, то $x(F1(x) ® F2(t)) также выводима” __F1(x) ® F2(t)__ $x(F1(x) ® F2(t)) 4) правила введения квантора существования: “если терм t входит в предикат f(t), то существует по крайней мере одна предметная переменная x, удовлетворяющая требованиям этого предиката F(x)” __F(t)__ $x(F(x)) 5) правила смены кванторов _"x(F(x))_ _$x(F(x))_ ù$x(ùF(x)) ; ù"x(Fù(x)) 6) правила переноса кванторов влево (формирование префикса) (их там очень много…) Приведённый набор правил облегчает эквивалентные преобразования формул в процессе логического вывода. В исчислении предикатов, как и в исчислении высказываний приняты 3 схемы формального вывода: заключения, теорема и противоречие. Вывод заключения из множества посылок записывается также, как и в исчислении высказываний (см. вопрос 6). 18. Исчисление предикатов. Принцип резолюции. Если в результате приведения к виду ПНФ матрица формулы M не будет содержать свободных переменных и сколемовских функций, то для вывода заключения полностью применим принцип резолюции исчисления высказываний (см. вопрос 9). Необходимо сформировать из матрицы множество дизъюнктов и сравнивая контрарные литеры получить пустую резольвенту . В результате приведения формулы к виду ССФ матрица формулы будет содержать сколемовские функции, где для получения контрарных литер необходимо выполнить операцию подстановки и замены термов предикатов. Т. о. главной проблемой принципа резолюции в исчислении предикатов является замена и подстановка термов. В случае решения этой задачи принцип резолюции применим также, как в исчислении высказываний. Принцип резолюции является более эффективной процедурой вывода, нежели дедуктивный вывод (процедура Эрбрана). Но он страдает существенным недостатком в формировании множества излишних и ненужных резольвент. 19. Исчисление предикатов. Расширение принципа резолюции (линейность и упорядоченность литер в дизъюнкте). см. вопрос 18, 10 Линейная резолюция может быть существенно усилена в исчислении предикатов введением понятия упорядоченного дизъюнкта и использование информации о резольвированных литерах. Идея метода заключается в рассмотрении дизъюнкта как последовательности литер, а не множества их. Отсюда упорядоченным дизъюнктом будем называть дизъюнкт с определённой последовательностью литер. При наличии в упорядоченном дизъюнкте двух одинаковых литер следует удалить старшую литеру, сохранив самую младшую. Другим усилением линейной резолюции является использование информации о резольвироваемых литерах. Обычно при выполнении процедуры резольвирования происходит удаление резольвируемых литер. Однако, оказывается, что –эти литеры несут полезную информацию, которая может быть использована для усиления линейной резолюции. Вместо удаления резольвируемых литер предлагается обрамлять их квадратом. Если за обрамлённой литерой в упорядоченном дизъюнкте не следует никакая другая литера, то её можно удалить. И наоборот, если за обрамлённой литерой в упорядоченном дизъюнкте следует никакая-либо литера, то её следует оставить для последующего использования. Используя резольвенты центрального стержня на предыдущих этапах резольвирования для сравнения с необрамлённой литерой в качестве боковых ветвей, можно получить все литеры упорядоченного дизъюнкта обрамлёнными квадратами. В этом случае можно удалить весь дизъюнкт.
Рис. 19.1. Линейная резолюция. 20. Исчисление предикатов. Подстановка и унификация. Подстановкой называют конечное множество вида θ = {t1/x1; t2/x2;… tn/xn}, где ti – терм, xi – предметная переменная, отличная от ti. Выполнив подстановку по всем предметным переменным, можно получить новые формулы, которые допускают унификацию в смысле формирования контрарных пар, т. е. P(x) Ú ùP(x) Множество подстановок можно формировать последовательно, просматривая каждый раз только одну предметную переменную. Рассмотренный метод имеет наиболее общий характер унификации и играет важную роль в языке Пролог, так как обобщает механизм вызова процедур, используемых в обычных языках программирования. Обычно аргументы вызова процедуры – это выражения, которые подставляют вместо формальных параметров и могут быть только именами переменных. Однако в прологе разрешается, чтобы сами формальные параметры были термами, и потому процесс вызова “логической процедуры” включает совмещение термов, являющихся аргументами вызова, с термами из заголовка вызова процедуры с помощью метода унификации. Если унификация оканчивается неудачей из-за того, что никакая подстановка не сможет совместить нужные литеры, то вызова не произойдёт, но будет сделана попытка совмещения с другим определением процедуры, если такая имеется. 21. Исчисление нечётких множеств. Основные понятия. Алгебра нечётких множеств. Если универсальное множество U разбить на подмножества Xi, то для каждого элемента u Î U может быть найдена функция принадлежности μxi(U): U ® [0; 1], характеризующая степень принадлежности этого элемента множеству Xi. Функция μxi принимает значение в интервале [0; 1]. Если носитель множества Xi состоит из единственного элемента u Î U, то такое множество называют одноэлементным нечётким множеством и обозначают Xi = μx(U)/u. Если функция принадлежности задана чётко, т. е. μxi(U) = 1, то имеем чёткое множество Xi = 1/u. Нечёткое множество нескольких (или многих) элементов можно рассматривать как объединение одноэлементных множеств и обозначить:
а при конечном числе элементов в виде:
Следует обратить внимание, что знаки + и ∑ в теории нечётких множеств используют для обозначения объединения, а не суммирования. Задание нечёткого множества выполняется экспертом по набору атрибутов, раскрывающих содержание понятия, нечёткого множества. При этом разные эксперты формируют различные подмножества на базе единого универсального множества. Всё это определяет слабость нечёткого исчисления и требует глубокого экспертного анализа правил отображения для формирования функции принадлежности. Практика показывает, что если ввести нечёткую переменную на универсальном множестве u Î U, то может быть построена достаточно “гладкая” функция принадлежности для всего универсального множества μ(U). Таким образом задача сводится к построению функции μ(U) по известному набору её значений в некоторых точках. Для решения поставленных задач подходят классические методы точечной аппроксимации, в частности метод наименьших квадратов. Этот метод позволяет получить достаточно гладкую функцию μ(U), которая равномерно приближается, в смысле среднего квадратичного отклонения, к заданному набору точек, необязательно совпадая с ними. Чаще всего определяют функцию μ(U) в виде обобщённого аппроксимирующего полинома:
где коэффициенты Ci определяют по условию:
Широкие возможности для приближённого описания фактов, явлений, событий, не поддающихся описанию в общепринятых количественных терминах, представляет лингвистическая переменная, которая отличается от числовой переменной тем, что её значениями являются слова в естественном или формализованном языке. Нечёткое множество лингвистической переменной X называют терм-множеством этой переменной T(X), а элементами множества являются лингвистические переменные Y со значениями, взятыми из универсального множества U, в качестве которого может быть использована базовая шкала лингвистической переменной X в интервале [0; 100] или [0; 1]. Как уже отмечалось, для каждой лингвистической переменной необходимо определить её совместимость с базовой шкалой лингвистической переменной X. Такая операция позволит определить функцию совместимости лингвистических переменных X и Y. На рис. 21.1. с помощью специалистов-экспертов построены графики, отражающие функции совместимости для каждой лингвистической переменной терм-множества лингвистической переменной “возраст”. Для этого использована базовая шкала возраста (0; 100).
рис. 21.1. Функция совместимости лингвистической переменной “возраст” Очевидно, что для функции совместимости также можно ввести предметную переменную и найти её аналитическое выражение, используя метод наименьших квадратов. Несколько сложнее построить функции совместимости и дать количественную оценку функции принадлежности для других приведённых лингвистических переменных. Для каждой нечёткой переменной могут быть найдены значения функции совместимости и сформировано нечёткое множество. Следует отметить, что для одного нечёткого множества сумма функций принадлежности всех его элементов не равна 1, а может быть больше или меньше 1. Набор фактов, явлений, событий, удовлетворяющих ограничениям, заданным функциями совместимости и принадлежности формируют кластер. Оценку каждого элемента кластера по функциям принадлежности формируют кластер. Оценку каждого элемента кластера по функциям принадлежности выполняют специалисты-эксперты методами экспертного анализа, а сама процедура формирования кластеров называется кластерным анализом. Алгебра нечётких множеств (см вопрос 22). 22. Исчисление нечётких отношений. Основные понятия. Алгебра нечётких отношений. Наряду с нечёткими множествами и нечёткими переменными в нечётком исчислении определённую роль играют нечёткие отношения, которые формируются в виде подмножества декартового произведения 2-х подмножеств, т. е. r: (X ® Y) Í X Ä Y. При этом функция принадлежности μr(x; y)/(x; y) характеризует степень принадлежности пары элементов (x; y) множеству r.
Если n-арное отношение r(x1, x2,… xn), то его функция принадлежности должна быть найдена для каждого набора переменных (x1i, x2i,… xni), т. е. μ(x1, x2,… xn)/(x1i, x2i,… xni). Над нечёткими множествами и отношениями выполняются такие же операции, как и над обычными (чёткими). Отличие заключается в определении функции принадлежности, которая принимает значение на интервале [0; 1]. Объединение нечётких множеств A и B есть множество C, состоящее из всех тех элементов универсального множества U, которые принадлежат хотя бы одному нечёткому множеству A или B:
Символ`Ú означает операцию выбора максимума из 2-х значений функций принадлежности μA(U) и μB(U). Поэтому функцию принадлежности элемента универсального множества U объединению двух нечётких множеств A и B равна максимальному значению функции принадлежности для 2-х множеств A и B, т. е.
Пересечение нечётких множеств A и B есть множество C, состоящее из всех тех элементов универсального множества U, которые принадлежат и к нечёткому подмножеству A, и к нечёткому подмножеству B.
Символ`&означает операцию выбора минимума из 2-х значений функций принадлежности μA(U) и μB(U). Поэтому функцию принадлежности элемента универсального множества U объединению двух нечётких множеств A и B равна минимальному значению функции принадлежности для 2-х множеств A и B, т. е.
Дополнение ùA есть нечёткое множество, состоящее из всех элементов универсального множества U, не принадлежащих нечёткому множеству A:
Функция принадлежности дополнения нечёткого множества μùA(U) определяется разностью функции принадлежности элемента универсальному множеству U, т. е. 1, и нечёткому множеству A, т. е. μA(U). Следовательно,
Разность нечётких множеств A и B есть множество C, состоящее из всех тех элементов универсального множества U, которые принадлежат к нечёткому подмножеству A и не принадлежат к нечёткому подмножеству B; используя правила эквивалентных преобразований формул множеств, можно определить значение функции принадлежности по ранее выведенным формулам:
Разность множеств можно определить, используя операции пересечения и дополнения:
Значение функции принадлежности элемента универсального множества U разности 2-х нечётких множеств A и B равно минимальному значению функций принадлежности для двух множеств A и B:
Симметрическая разность нечётких множеств A и B есть множество C, состоящее из всех тех элементов универсального множества U, которые принадлежат к нечёткому подмножеству A и не принадлежат к нечёткому подмножеству B или принадлежат к нечёткому подмножеству B и не принадлежат к нечёткому подмножеству A; используя правила эквивалентных преобразований формул множеств, можно определить значение функции принадлежности по ранее выведенным формулам: Для C = ADB = (A Ç ùB) È (B Ç ùA) =
Значение функции принадлежности элемента универсального множества U симметрической разности 2-х нечётких множеств A и B равно максимальному значению двух минимальных значений для пересечения множеств (A Ç ùB) и (B Ç ùA):
Это правило получило название “максимина”. Возведение в степень нечёткого множества A формирует две операции: концентрации и растяжения.
Операция концентрации.
Значение функции принадлежности определяется по формуле:
Для лингвистической переменной эта операция выражается добавлением слова “очень”. Операция растяжения нечёткого множества
Значение функции принадлежности определяется по формуле:
Операция контрастной интенсивности увеличивает значения функции принадлежности, которые > 0,5 и уменьшает значения функции принадлежности, которые < 0,5, уменьшая т. о. размытость нечёткого множества:
Декартово произведение нечётких множеств A и B есть множество, обозначаемое A Ä B и состоящее из всех тех или только тех упорядоченных пар (a; b), первая компонента которых принадлежит множеству A, а вторая – множеству B.
Значение функции принадлежности определяется по формуле:
23. Логика нечётких высказываний. Основные понятия. Известно, что для исчисления обычных (чётких) высказываний приняты только два значения истинности суждения: true или false. Для нечётких высказываний значение истинности определяется степенью принадлежности элемента к нечёткому множеству A, т. е. μA(U). Поэтому значение истинности о принадлежности элемента к множеству A, т. е. ρA(U), также принадлежит интервалу [0; 1]. Можно утверждать, что истинность высказывания есть также нечёткое дискретное множество. Для непрерывного определения значения истинности также можно применить функцию совместимости терм-множества “истинность” с базовой шкалой и построить график функции совместимости. При формировании сложного высказывания значение истинности зависит от вида логической связки между его составляющими и видом алгебраической операции, выполняемой над нечёткими множествами. Так значение истинности высказывания о принадлежности элемента объединению, пересечению или дополнению нечётких множеств определяется степенью принадлежности элемента результатам исполнения этих операций. Поскольку в нечётком исчислении значение истинности высказывания принадлежит интервалу [0; 1], то невозможно построить таблицы истинности для нечётких высказываний. Основным правилом вывода заключения, как и в обычном (чётком) исчислении является modus ponens, согласно которому судить о значении истинности заключения B можно по значениям истинности A и импликации (A ® B). 24. Выбор решения при нечётком выводе заключения. В результате исполнения алгебраических или логических операций над нечёткими множествами будут получены также нечёткие множества результатов этих операций. Для выбора конкретного решения из числа элементов нечёткого множества используют понятие “степень разделения” - α. Сравнивая значение функции принадлежности каждого элемента нечёткого множества с заданным значением (т. е. μA(U) ≥ α или μA(U) ≤ α), можно разделить это множество на два подмножества, одно из которых имеет функции принадлежности элементов больше заданного значения α, а другое – меньше. Изменяя степень разделения множества можно формировать уровни определённости решения в виде дерева решений. Корнем этого дерева будет исходное нечёткое множество, а ветви и уровни будут формироваться заданным значением α. Пусть A и B принадлежат универсальному множеству U. Соответствующие множества α-уровня определяются следующим образом: A’ = {U| μA(U) ≥ α}; B’ = {U| μB(U) ≤ α}, где μA(U), μB(U) – функции принадлежности. Если каждый элемент A’ больше любого элемента B’, т. е. UA’ > UB’ для UA’ Î A’ и UB’ Î B’, то A больше B на уровне α. 25. Реляционная логика. Основные понятия. Известно, что соответствие, заданное на элементах одного множества X, называют отношением (relation). Правила, заданные отношением, формируют множество упорядоченных последовательностей элементов множества X. В свою очередь это множество является подмножеством декартового произведения множества X, т. е. rel = {<x1, x2,… xn>|xi Î X} Í Än X Упорядоченная последовательность <x1, x2,… xn> называется кортежем, а его отдельные элементы – компонентами кортежа. Кортежи принято обозначать символами t Î T, где T – множество кортежей. Число компонент кортежа определяет его длину или арность. Таблица – наиболее удобная форма отображения отношения. Если столбцами таблицы являются некоторые подмножества множества X, а элементами таблицы – значения элементов множества X, то строками являются кортежи заданного отношения. Область определения значений компонентов кортежа принято называть доменом и обозначать Di. Признак, по которому выделена область определения компоненты кортежа – домен – называют атрибутом и обозначают символом Ii. Значение атрибута, взятое из домена, выделяет объект реального мира из множества ему подобных по данному признаку. Последовательная запись атрибутов, заданная декартовым произведением доменов формирует схему отношения, т. е. Sch(r) = r(I1, I2,… Ik) = R Каждая область определения значений атрибутов может быть поименована, что существенно облегчает организацию обработки данных. Несколько атрибутов могут иметь единую область определения их значений (один домен), но не наоборот. Набор кортежей одного отношения формирует тело таблицы, место атрибута в которой задано схемой отношения, а его значение – областью определения Di. Количество используемых в отношении атрибутов (столбцов таблицы) определяет его арность, а число кортежей – мощность. Итак, одним из способов задания и описания отношения является таблица, “шапка” которой формируется схемой отношения, а “тело” есть множество кортежей, описывающих множество объектов реального мира. Схема отношения задаёт строгий порядок компонент кортежа, не допуская их перестановки и/или удаления из кортежа. Атрибуты кортежа должны зависеть только от ключа отношения, в противном случае отношение следует декомпозировать на 2 и более отношений. 26. Реляционная алгебра. Основные и дополнительные унарные операторы. Произвольное множество X с заданной на нём совокупностью операций, обеспечивающих функциональное отображение Г: Xn ® X, называют алгеброй. При этом множество X называют основным множеством алгебры, знаки алгебраических операций – операторами, а объекты множества X, над которыми выполняются алгебраические преобразования – операндами. Если в качестве множества X использовать множество отношений, а в качестве алгебраических операций такие преобразования, которые обеспечивают формирование новых отношений, то получим особый тип алгебр – реляционную алгебру. Всё множество операторов реляционной алгебры можно представить 2-мя классами: унарные (1 операнд) и бинарными (2 операнда). Основные унарные операторы. Оператор выбора δB(r) (Selection (отношение, условия)) позволяет извлекать из данного отношения r кортежи, удовлетворяющие условию B, и формировать новое отношение r’. Условия представляют собой выражения, которые могут включать только операторы сравнения множества θ = {=, ≠, >, ≥, <, ≤}, между текущими и заданными значениями атрибутов, а также логические операторы для формирования сложных условий из множества Σ = {& , Ú, ù}. В то же время использование функциональных символов в формировании условий запрещено. Оператор проекции πR’(r) (Projection(отношение, список_атрибутов)) позволяет формировать из данного отношения r новое отношение r’ путём удаления и (или) переупорядочения атрибутов в соответствии с заданной схемой нового отношения R’. Для выполнения этой операции должна быть прежде всего задана схема генерируемого отношения R’ = Sch(r’). Дополнительные унарные операторы. Оператор добавления (ADD (r; I1 = d1; I2 = d2;… Im = dm)) предусматривает добавление кортежа в заданное отношение. Для этого должно быть указано имя отношения и значения всех компонент кортежа, который необходимо включить в отношение. В случае, когда порядок атрибутов строго фиксирован, разрешается не указывать имена атрибутов, а только лишь их значения, т. е. ADD (r; d1; d2;… dm). Оператор добавления (DEL (r; I1 = d1; I2 = d2;… Im = dm)) определяет исполнение операции удаления кортежа из данного отношения. Для этого должно быть указано имя отношения и значения всех компонент кортежа. В случае, когда порядок атрибутов строго фиксирован, разрешается не указывать имена атрибутов, а только лишь их значения, т. е. DEL (r; d1; d2;… dm). В большинстве баз для этого используют ключ, когда достаточно указать имя отношения и значение ключа. Оператор изменения (CH (r, I1 = d1; I2 = d2; … Ii = di; … Ij = dj; … IiH = diH; IjH = djH)) позволяет выполнять изменение значений некоторых атрибутов кортежа. Для этого достаточно указать имя отношения, ключ записи кортежа, имя атрибута и его прежнее и новое значения. Но наиболее полно этот оператор использует запись всей строки таблицы с указанием всех значений атрибутов прежнего значения кортежа и новых значений атрибутов. 27. Реляционная алгебра. Основные бинарные операторы. см. вопрос 26. Оператор объединения È(r1, r2) (Union (отношение_1, отношение_2)) для двух отношений, имеющих одинаковые схемы, формирует новое отношение, объединяя все кортежи первого и второго отношений. При этом одинаковые кортежи двух отношений “сливаются” в один кортеж нового отношения. Оператор разности \(r1; r2) (Difference (отношение_1, отношение_2)) для двух отношений, имеющих одинаковые схемы, формирует новое отношение, выбирая из первого отношения только те кортежи, которых нет во втором отношении. Оператор декартова произведения Ä(r1; r2) (Product (отношение_1, отношение_2)) формирует из двух отношений r1 и r2 арности n1 и n2 новое отношение арности (n1 + n2). При этом первые n1 компонентов кортежа нового отношения r’ образованы, принадлежащими r1, а последние n2 компонентов – кортежами, принадлежащими отношению r2. Число кортежей нового отношения r’ определяется произведением числа кортежей первого и второго отношений, т. к. каждый кортеж первого отношения должен быть соединён со всеми кортежами второго отношения. 28. Реляционная алгебра. Дополнительные бинарные операторы. см. вопрос 26. Оператор пересечения Ç(r1, r2) (Intersection (отношение_1, отношение_2)) для двух отношений, имеющих одинаковые схемы, формирует новое отношение, выбирая только одинаковые кортежи из первого и второго отношений. Оператор естественного соединения ><(r1, r2) (Join (отношение_1, отношение_2)) формирует из 2-х отношений r1 и r2, имеющих один или несколько одинаковых имён атрибутов, новое отношение r’, схема которого есть объединение атрибутов 2-х исходных отношений, а кортежи формируются из кортежей первого отношения, присоединяя кортежи 2-го отношения по одинаковым значениям одноимённых атрибутов. Для практического определения естественного соединения необходимо: a) найти декартово произведение 2-х отношений r1 и r2; b) совместить одноимённые столбцы декартова произведения; c) удалить строки, имеющие различные значения атрибутов в совмещённых столбцах. Оператор θ-соединения >B<(r1, r2) (Join (отношение_1, отношение_2, условие)) формирует из 2-х отношений r1 и r2 арности n1 и n2 новое отношение r’ арности (n1 + n2), обеспечивая условие. Для практического определения θ-соединения необходимо: a) найти декартово произведение 2-х отношений r1 и r2; b) соединить строки первой и второй таблиц отношений r1 и r2, если выполняется условие арифметического сравнения значений d1i и d2j-го атрибутов первого и второго отношений.
29. Реляционное исчисление (РИ) с переменными-кортежами. РИ с переменными-кортежами определяет способы и приёмы формирования выражения {t’|F(t)}, где t – переменная-кортеж фиксированной длины; F(t) – формула логической функции, построенная из атомов и совокупности арифметических и логических операторов. Предметными переменными и предметными постоянными РИ являются кортежи. Для обозначения переменных кортежей дополнительно используем символы x и y, а для постоянных – u и v. Атом определяется следующими правилами: 1) если r – имя отношения, а x – переменный кортеж, то r(x) – атом; 2) если x и y – переменные кортежи, v Î θ – арифметический оператор (знак сравнения), Ii и Ij – атрибуты, то x(Ii) v y(Ij), x(Ii) v kdi, kdi v y(Ij) – атомы; 3) никаких других атомов нет. При записи формул используют понятия “свободных” и “связных” переменных-кортежей, что определяется характером использования кванторов – логических операторов, переводящих одну высказывательную форму об отношении в другую. Различают кванторы общности – “все”, “всякий” и т. п. и существования – “некоторые”, “хотя бы один” и т. п. Переменная-кортеж в формуле является связанной, если ей предшествует квантор общности или существования по этой же переменной. В противном случае имеем свободную переменную – кортеж. Наличие связанной переменной формирует класс разрешённых формул. Формулы исчисления с переменными-кортежами могут быть построены из атомов рекурсивно: 1) всякий атом есть формула, т. е. F; 2) если F1 и F2 – формулы, то (ùF1), (F1 Ú F2), (F1 & F2) также формулы; 3) если x – переменный кортеж, F – формула, включающая x, то $x(F) и "x(F) также формулы; 4) никаких других формул нет. Итак {t’|F(t)} есть выражение РИ с переменными-кортежами, где t – единственная свободная переменная-кортеж в F(t). 30. Реляционное исчисление (РИ) на доменах. РИ на доменах строится на тех же операторах, что и РИ с переменными-кортежами (см. вопрос 29). Однако в этом исчислении не существует переменных-кортежей, а существуют переменные на доменах, которые являются лишь компонентами кортежей. Для обозначения переменных на доменах используем символы x и y, а для обозначения постоянных – kdi. Атом имеет вид: 1) если r – отношение со схемой Sch(r) = (I1, I2, … In), то r(x1, x2, … xn) – атом, где каждая Xi есть постоянная или переменная на доменах. 2) если x и y – переменные на доменах, v Î θ – арифметический оператор (знак сравнения), то (x v y), (x v kdi), (kdi v y) – атомы; 3) никаких других атомов нет. r(x1, x2, … xn) указывает на то, что значения тех xi, которые являются переменными на доменах, должны быть выбраны так, чтобы <x1, x2, … xn> был кортежем отношения r, а смысл атома (x v y) заключался в том, что x и y представляют собой значения, при которых (x v y) истинно. В записи формул также используют понятия “свободных” и “связных” переменных при использовании логических операторов – кванторов, переводящих одну высказывательную форму в другую. Правила для определения свободных и связанных переменных остаются теми же, что в исчислении переменных-кортежей. Формулы РИ с переменными на доменах могут быть построены из атомов рекурсивно: 1) всякий атом есть формула F; 2) если F1 и F2 – формулы, то (ùF1), (F1 Ú F2), (F1 & F2) также формулы; 3) если x – переменный на доменах, F – формула, включающая x, а I – атрибут из U, то F(x(I)) также формула; 4) никаких других формул нет. Разрешённые формулы РИ на доменах требуют, чтобы переменная, связываемая квантором, входила свободно в формулу, следующую за квантором. Выражения РИ переменных на доменах имеет вид: {<x1(I1), x2(I2), … xn(In)>|F(x1, x2, … xn)}, где F(…) – разрешённая формула; xi – свободные переменные, входящие в F(…); I1, I2, … In – атрибуты из U. 31. Грамматика формального языка БНФ. Для строгого и точного описания синтаксиса языка удобно использовать какой-либо метаязык. Наиболее распространенным среди них является язык формул Бэкуса-Наура (язык БНФ или Бэкуса нормальная форма). На языке БНФ синтаксис языка описывается в виде некоторых формул, весьма похожих на обычные математические формулы. Введем условные обозначения: ::= - знак о том, что выражение, стоящее слева, может быть замещено выражением, стоящим справа ( "...состоит из..."); < .. > - синтаксическая переменная языка; " .. " - слово (лексема) языка <.. ><.. >.. - соединение синтаксических переменных союзом "и"; <.. > | <.. >l .. - разделение синтаксических переменных разделителем "или"; " .. " <.. >.. I <.. > ".. ".. - соединение синтаксических переменных и лексем союзом "и" и разделение выражений и/или предложений языка разделителем "или"; " .. " " .. " .. - соединение лексем союзом "и" ".. " | ".. " | .. - разделение лексем разделителем "или"; { .. } - многократное повторение выражения, заключенного в фигурные скобки, включая нуль раз; [ ... ] - одно- или нулькратное повторение выражения, заключенного в прямоугольные скобки. Тогда основная формула БНФ может быть представлена в виде X ::= Y1 | Y2 | Y3 |..., где X – выражение, определяемое только синтаксической переменной; Yi – выражение, определяемое набором синтаксических переменных и/или лексем, где I = 1, 2, 3, ... При подстановке вместо X выражений Yi осуществляется вывод синтаксически правильной конструкции выражения или предложения, описываемого синтаксической переменной X. Следует обратить внимание, что в левой части каждого правила находится только одна синтаксическая переменная, а в правой выражение, включающее цепочки синтаксических переменных либо наборы лексем естественного языка. Знак "|" в правой части правил показывает возможность выбора значения синтаксической переменной, указанной в левой части. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|