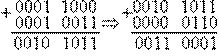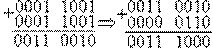Представление дробных чисел

В двоичном коде с фиксированной

Запятой

Следующий вид двоичных кодов, который мы рассмотрим - это дробные коды. Как и в случае целых чисел, дробные числа могут быть беззнаковые и знаковые. Для записи знаковых чисел могут быть использованы прямые, обратные и дополнительные коды. Принцип их построения точно такой же, как и в случае целых чисел.

Рассмотрим, как можно записать дробное число. До сих пор мы предполагали, что двоичная запятая находится правее самого младшего разряда. Но можно договориться, что запятая находится слева от самого старшего разряда, и тогда в такой форме можно будет записывать только дробные числа:

Рис. 3.5.

Или договоримся, что запятая находится точно посередине переменной, и тогда мы сможем записывать смешанные числа (рис. 3.6):

Рис. 3.6.

Представление чисел в двоичном

Коде с плавающей запятой

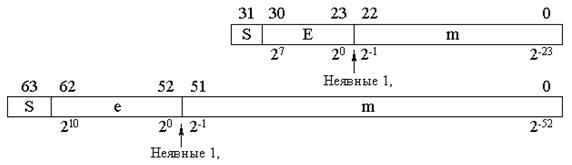
Часто приходится обрабатывать очень большие числа или наоборот очень маленькие числа. При таких вычислениях пришлось бы использовать числа с очень большой разрядностью. Для вычислений с такими величинами числа с фиксированной запятой неэффективны.

В десятичной арифметике для записи таких чисел используется алгебраическая форма. При этом число записывается в виде мантиссы, умноженной на 10 в степени, отображающей порядок числа, Например:

0,2∙10⁵; 0,16∙10^-38.

Для записи двоичных чисел тоже используется такая форма записи. Эта форма записи называется запись числа с плавающей точкой. Напомним, что мантисса не может быть больше единицы и после запятой в мантиссе не может записываться ноль.

А теперь рассмотрим промышленные стандарты, используемые для представления чисел в компьютерах. Существует стандарт IEEE 754 для представления чисел с одинарной точностью (float) и с двойной точностью (double). Для записи числа в формате с плавающей запятой одинарной точности требуется тридцатидвухбитовое слово. Для записи чисел с двойной точностью требуется шестидесятичетырёхбитовое слово. Чаще всего числа хранятся в нескольких соседних ячейках памяти процессора. Форматы числа в формате с плавающей запятой одинарной точности и числа в формате с плавающей запятой удвоенной точности приведены ниже (рис. 3.7).

Рис. 3.7.

На рисунке буквой S обозначен знак числа, 0 - это положительное число, 1 - отрицательное число. e обозначает смещённый порядок числа. Смещение требуется, чтобы не вводить в число еще один знак. Смещённый порядок всегда положительное число. Для одинарной точности для порядка выделено восемь бит. Для смещённого порядка двойной точности отводится 11 бит. Для одинарной точности смещение принято 127, а для двойной точности - 1023. В десятичной мантиссе после запятой могут присутствовать цифры 1:9, а в двоичной - только 1. Поэтому для хранения единицы после двоичной запятой не выделяется отдельный бит в числе с плавающей запятой. Единица подразумевается, как и двоичная запятая. Кроме того, в формате чисел с плавающей запятой принято, что мантисса всегда больше 1. То есть диапазон значений мантиссы лежит в диапазоне от 1 до 2.

Рассмотрим несколько примеров:

Пример 3.6. Определить число с плавающей запятой, лежащее в четырёх соседних байтах:

11000001 01001000 00000000 00000000.

- Знаковый бит, равный 1 показывает, что число отрицательное.

- Экспонента 10000010 в десятичном виде соответствует числу 130. Вычтя число 127 из 130, получим число 3.

- Теперь запишем мантиссу: 1,100 1000 0000 0000 0000 0000

- И, наконец, определим десятичное число: 1100,1b = 12,5d

Пример 3.7. Определить число с плавающей запятой, лежащее в четырёх соседних байтах:

11000011 00110100 00000000 00000000

- Знаковый бит, равный 1 показывает, что число отрицательное.

- Экспонента 10000110 в десятичном виде соответствует числу 134. Вычтя число 127 из 134, получим число 7.

- Теперь запишем мантиссу: 1,011 0100 0000 0000 0000 0000

- И, наконец, определим десятичное число: 10110100b=180d

Для того чтобы записать ноль, достаточно записать в смещенный порядок число 00000000b. Значение мантиссы при этом не имеет значения. Число, в котором все байты равны 0, тоже попадает в этот диапазон значений.

Бесконечность соответствует смещенному порядку 11111111b и мантиссе, равной 1,0. При этом существует минус бесконечность и плюс бесконечность (переполнение и антипереполнение), которые иногда отображаются на экране монитора как +INF и -INF.

Запись десятичных чисел

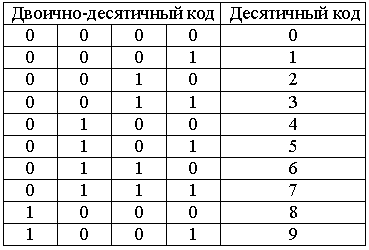
Иногда бывает удобно хранить числа в памяти процессора в десятичном виде (например, для вывода на экран дисплея). Для записи таких чисел используются двоично-десятичные коды. Для записи одного десятичного разряда используется четыре двоичных бита. Эти четыре бита называются тетрадой. При помощи четырех бит можно закодировать шестнадцать цифр. Лишние комбинации в двоично-десятичном коде являются запрещенными. Таблица соответствия двоично-десятичного кода и десятичных цифр приведена ниже (табл. 3.1):

Табл. 3.1.

Остальные комбинации двоичного кода в тетраде являются запрещенными. Запишем пример двоично-десятичного кода:

1258 = 0001 0010 0101 1000

589 = 0000 0101 1000 1001.

Достаточно часто в памяти процессора для хранения одной десятичной цифры выделяется одна ячейка памяти (восьми, шестнадцати или тридцатидвухразрядная). Это делается для повышения скорости работы программы. Для того, чтобы отличить такой способ записи двоично-десятичного числа от стандартного, способ записи десятичного числа, как это показано в примере, называется упакованной формой двоично-десятичного числа.

Суммирование двоично-

Десятичных чисел

Суммирование двоично-десятичных чисел можно производить по правилам обычной двоичной арифметики, а затем производить двоично-десятичную коррекцию. Двоично-десятичная коррекция заключается в проверке каждой тетрады на допустимые коды. Если в какой либо тетраде обнаруживается запрещенная комбинация, то это говорит о переполнении. В этом случае необходимо произвести двоично-десятичную коррекцию. Двоично-десятичная коррекция заключается в дополнительном суммировании числа шесть (число запрещенных комбинаций) с тетрадой, в которой произошло переполнение или произошёл перенос в старшую тетраду.

Пример 3.8:

Пример 3.9:

3.8. Арифметико-логические

устройства

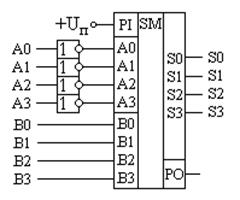
Выше были рассмотрены схемы суммирования многоразрядных кодов. Однако кроме суммирования часто требуется осуществлять и вычитание двоичных кодов. Двоичные коды, при помощи которых можно записывать отрицательные числа уже рассматривались в предыдущих разделах. Там же было показано, что при использовании дополнительных кодов операцию вычитания двух положительных чисел можно заменить операцией суммирования положительного и отрицательного числа, при этом получение отрицательного числа из положительного числа является элементарной операцией. Для этого необходимо проинвертировать число и прибавить к нему 1.

Схема устройства вычитания числа A из числа B приведена на рис. 3.8, а схема вычитателя числа B из числа A приведена на рис. 3.9.

Рис. 3.8. Схема вычитателя числа A из числа B

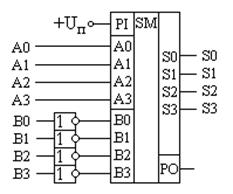
Рис. 3.9. Схема вычитателя числа B из числа A

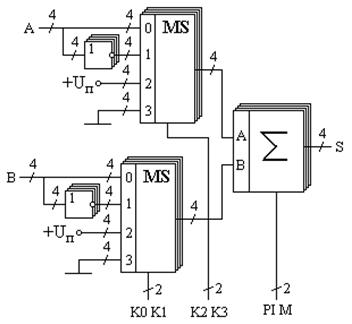
Если же потребуется в процессе вычислений изменять арифметическую операцию, то в схему можно ввести коммутатор. Такая схема приведена на рис. 3.10.

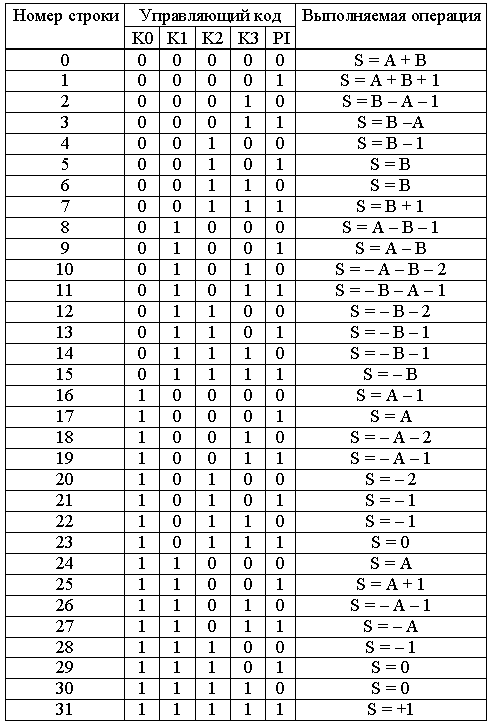
Рис. 3.10. Структурная схема арифметического устройства

В приведённой на рис. 3.10 схеме используются четырёхвходовые коммутаторы, для управления каждым из которых достаточно двух бит. То есть для управления всей схемы в целом достаточно четырёх проводов управления. Попытаемся построить таблицу операций, которые будет выполнять эта схема. На результат операции будет влиять вход переноса сумматора PI, поэтому этот провод тоже включим в состав кода, управляющего схемой. Операции, которые выполняются арифметической схемой в зависимости от поданного на управляющие линии кода, приведены в табл. 3.2.

Табл. 3.2.

Проанализируем эту таблицу. Если на все управляющие входы подать низкий потенциал, то к входу сумматора будут подключены коды A и B без инверсии. В этом случае будет производиться операция суммирования. Эта ситуация отображена первыми двумя строками таблицы выполняемых операций. Операция вычитания осуществляется второй, третьей, восьмой и девятой строкой. В этом случае один из операндов поступает на вход сумматора через блок инверторов. Правда для получения дополнительного кода не хватает единицы, но её можно подать на вход переноса сумматора PI. Ещё одной часто используемой операцией является увеличение числа на единицу или уменьшение числа на единицу. Эти операции позволяют легко организовывать циклы в программе и переходить от предыдущего операнда к следующему. Такие операции могут быть выполнены при помощи кодов, записанных в строках четыре, семь, шестнадцать и двадцать пять. Кроме того, схема арифметического устройства может просто передавать на выход любой из входных кодов без изменения, что позволяет осуществлять копирование данных (суммирование с константой ноль) через это устройство без дополнительных схем коммутации.

При небольшом изменении схемы такое устройство может быть преобразовано в схему, которая позволяет осуществлять не только арифметические, но и логические операции. Для этого нужно вести дополнительный коммутатор, который будет разрывать цепи переноса между разрядами. Эта управляющая цепь обычно называется M.

Подчеркнём основную особенность полученного устройства. Арифметико-логические устройства позволяют выбирать вид выполняемой операции при помощи кода, подаваемого на специальные ножки микросхемы. Это позволяет программировать одно и то же устройство для выполнения различных функций. Разработка такого устройства позволило обменивать большую скорость выполнения отдельных операций на сложность реализуемого алгоритма, что, в конце концов, привело к разработке микропроцессорных систем.

КОНТРОЛЬНЫЕ ВОПРОСЫ:

1. Беззнаковые двоичные коды.

2. Знаковые обратные двоичные коды.

3. Знаковые дополнительные двоичные коды.

4. Представление дробных чисел в двоичном коде с фиксированной

запятой.

5. Представление чисел в двоичном коде с плавающей запятой.

6. Запись десятичных чисел.

7. Суммирование двоично-десятичных чисел.

8. Арифметико-логические устройства.

4. МИКРОПРОЦЕССОРНЫЕ

СИСТЕМЫ И МИКРО-ЭВМ

Не нашли, что искали? Воспользуйтесь поиском по сайту: