
|
|
Для сигналов с ограниченным спектром теорема отсчетов имеет вид
и называется формулой Котельникова. При дискретизации сигнала появляется погрешность, обусловленная конечным временем одного преобразования и неопределенностью момента времени его окончания. В результате вместо равномерной дискретизации получаем дискретизацию с переменным периодом. Такая погрешность называется апертурной. Если считать, что апертурная погрешность определяется скоростью изменения сигнала, то ее можно определить по формуле
где Та - апертурное время, u'(tn) - скорость изменения сигнала в момент времени tn, т. е.
Для гармонического сигнала u(t) = Um sinwt максимальное значение апертурной погрешности получим при условии u'(t)=Um, т. е. при coswt = l. Относительная апертурная погрешность в этом случае будет иметь значение
Сравнивая период дискретизации, определенный по теореме отсчетов, с апертурным временем (2.1), получим
откуда следует, что для снижения апертурной погрешности приходится в p/d раз увеличивать частоту преобразования АЦП. Так, например, при дискретизации гармонического сигнала с частотой fm = 10кГц по теореме отсчетов достаточно иметь максимальную частоту АЦП Fm = 2fm = 20кГц, при погрешности da = 10-2, необходимо увеличить эту частоту до значения 2 fm p/d = 20∙103p/10-2 = 6,3 MГц. В отличие от дискретизации, которая теоретически является обратимой операцией, квантование представляет собой необратимое преобразование исходной последовательности и сопровождается появлением неизбежных погрешностей. Характеристика идеального квантователя приведена на рис. 2.2 б. При равномерном квантовании расстояние между двумя соседними значениями делается постоянным, как показано на рис. 2.1 б. Разность между двумя соседними значениями квантованной величины называется шагом квантования h. По существу квантование представляет собой операцию округления непрерывной величины до ближайшего целого значения. В результате максимальная погрешность квантования равна ±0,5 h (рис. 2.1 б). Однако при преобразовании произвольного сигнала максимальная погрешность встречается сравнительно редко, поэтому в большинстве случаев для оценки качества АЦП используют не максимальную, а среднеквадратическую погрешность Выходной величиной АЦП является цифровой код, т. е. последовательность цифр, с помощью которой представляются дискретные квантованные величины. В АЦП используют четыре основных типа кодов: натуральный двоичный, десятичный, двоично-десятичный и код Грея. Кроме этого, АЦП, предназначенные для вывода информации в десятичном коде, выдают на своем выходе специализированный код для управления семисегментными индикаторами. Большинство АЦП работают с выходом в натуральном двоичном коде, при котором каждому положительному числу N ставится в соответствие код {bi}=b1, b2, ..., bn, где bi равны нулю или единице. При этом положительное число в двоичном коде имеет вид
Такой код принято называть прямым: его крайний правый разряд является младшим, а крайний левый - старшим. Прямой код пригоден лишь для работы с однополярными сигналами. Полный диапазон преобразуемого сигнала равен 2n, a N =2n-1. Двоичные числа, используемые в АЦП, как правило нормализованы, т. е. их абсолютное значение не превышает единицы. Они представляют собой отношение входного сигнала к полному диапазону:
Если АЦП должен работать с двуполярными числами, то наиболее часто используют дополнительный код, который образуется вычитанием преобразуемого числа С из постоянной величины 2n+1. Диапазон представления чисел в двоичном коде имеет значение от 2-m до 1-2-m. Нуль имеет одно значение 000...0. При использовании в АЦП двоично-десятичных кодов каждая десятичная цифра представляется четырьмя двоичными знаками и содержит десять значений от 0 до 9. Так, например, десятичное число 10 можно представить как 0001 0000, а число 99 можно представить в виде 1001 1001. Так как при кодировании четырьмя двоичными знаками можно получить 16 кодовых значений, то приведенное двоично-десятичное представление не является единственным. Наиболее широко используют коды, в которых цифрам в тетрадах присваивают веса 8-4-2-1 или 2-4-2-1:

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
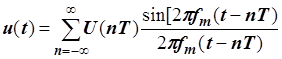
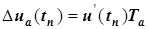
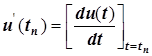
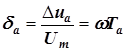 . (2.1)
. (2.1) ,
, , которая примерно в 3,5 раза меньше максимальной. В АЦП погрешность квантования определяется как единица младшего значащего разряда (ЕМР).
, которая примерно в 3,5 раза меньше максимальной. В АЦП погрешность квантования определяется как единица младшего значащего разряда (ЕМР). . (2.2)
. (2.2) .
.