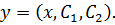|
|
Свойства определённого интеграла1. 3. Геометрическое приложение определенного интеграла (площадь криволинейной трапеции). Рассмотрим фигуру Рис. 8.1. Криволинейная трапеция Фигура, ограниченная снизу отрезком [a; b] оси Ox, сверху графиком непрерывной функции y = f(x) такой, что f (x) ≥ 0 при х Отрезок [a; b] называют основанием этой криволинейной трапеций. Площадь криволинейной трапеции вычисляется по формуле:
Таким образом, геометрический смысл определенного интеграла заключается в вычислении площади криволинейной трапеции. Приведём различные примеры криволинейной трапеции:
Рассмотрим основные способы вычисления площади криволинейной трапеции:
Алгоритм нахождения площади криволинейной трапеции: 1. Построить графики функции; 2. Определить пределы интегрирования a и b; 3. Выбрать и записать соответствующую формулу площади криволинейной трапеции; 4. Вычислить площадь криволинейной трапеции.
ПРИМЕР : Вычислить площадь криволинейной трапеции, ограниченной осью Ох, прямыми х = -1, х = 2 и параболой y = 9 - x2. Решение: Построим график функции y = 9 - x2 и изобразим данную криволинейную трапецию:
координаты вершины:
(0 ; 9) - вершина Точки пересечения с осью Ох: 9 - x2 = 0 -x2 = 9 x2 = 9 => x1/2 = Проведём прямые х = - 1 и х = 2 f(x)=9 - x2 a = - 1 b = 2 Формула для вычисления площади криволинейной трапеции:
Ответ: Sкр.тр = 24(кв.ед) Лекция 9. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
Дифференциальные уравнения первого порядка Рассмотрим дифференциальное уравнение: y′= f(x,y) начальное условие Коши к нему имеет вид:
Общее решение дифференциального уравнения y′=f(x,y) имеет вид y=φ(x,C), где C – произвольная постоянная. Оно определяет семейство интегральных кривых. Частное решение – это одна интегральная кривая, проходящая через точку, заданную начальным условием.
Дифференциальные уравнения первого порядка с разделяющимися переменными: А) Если в дифференциальном уравнении y′=f(x,y) функция f(x,y) может быть представлена в виде: Его решение (интегрирование) проводится по следующему алгоритму: 1. Представим
2. Разделить переменные: 3. Проинтегрировать обе части равенства:
где С – произвольная постоянная. Это общий интеграл уравнения, входящие в него неопределенные интегралы находятся методами, рассматриваемыми в интегральном исчислении.
Б) Если дифференциальное уравнение записано в виде:
то это уравнение с разделяющимися переменными, если
Интегрирование уравнения производится так:
Считая
Интегрируя обе части получим:
Заметим, при разделении переменных могут быть «потерянные» решения, которые в некоторых случаях будут особыми решениями.
Пример: Найти общее решение дифференциального уравнения
Решение: Так как
Это дифференциальное уравнение с разделяющимися переменными. Разделим переменные (у – влево, х - вправо) и получим:
Проинтегрируем обе части дифференциального уравнения:
Рассмотрим решение каждого из интервалов отдельно:
Тогда, получим
Ответ:
Пример: Найти частное решение дифференциального уравнения с разделяющимися переменными, удовлетворяющее начальному условию
Решение: Проинтегрируем обе части дифференциального уравнения:
Рассмотрим решение каждого из интервалов отдельно:
Тогда, получим
Чтобы найти частное решение ДУ надо найти значение С при условии, что
Тогда частное решение ДУ имеет вид:
Ответ:
Дифференциальные уравнения второго порядка В общем виде дифференциальное уравнение второго порядка записывается так:
Если это уравнение можно разрешить относительно производной второго порядка, то оно примет нормальный вид:

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
 , где С - константа
, где С - константа

 [a; b] и f (x) > 0 при х
[a; b] и f (x) > 0 при х  (а; b), а с боков ограниченная отрезками прямых х = а и x = b, называется криволинейной трапецией.
(а; b), а с боков ограниченная отрезками прямых х = а и x = b, называется криволинейной трапецией.



 или
или


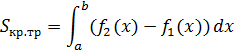


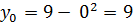
 3
3
 .
. , т.е.
, т.е.  при
при 
 , то уравнение называется уравнением с разделяющимися переменными.
, то уравнение называется уравнением с разделяющимися переменными.


 ,
, ,
, ;
; 
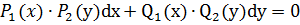 ;
; , разделим на
, разделим на  :
:
 - общий интеграл уравнения.
- общий интеграл уравнения.



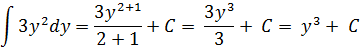



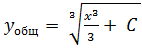
 при
при 
 ,
, 


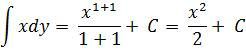





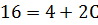
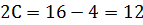




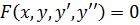
 а его общее решение содержит две произвольных постоянных:
а его общее решение содержит две произвольных постоянных: