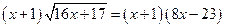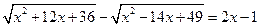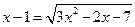|
|
III Изучение нового материала.12 Нестандартные методы решения иррациональных уравнений. 4. Умножение на сопряжённое выражение. 5. Переход к модулю. 6. Использование свойств функции: § Область определения функции (ОДЗ) § Область значения функции § Свойство ограниченности функции (метод оценок) § Свойство монотонности § Использование суперпозиций функций · Умножение на сопряжённое выражение. Воспользуемся формулой Пример 8: Умножим обе части уравнения на сопряжённое выражение:
Проверка показывает, что число является корнем. Ответ: · Переход к модулю. Для этого метода воспользуемся тождеством: Пример 9:
Рассмотрим случаи: § Если
§ Если
2=6( ложно) § Если
Ответ: -3;3 · Использование свойств функции: § Область определения функции (ОДЗ) Иногда нахождение области определения функций, входящих в уравнение, существенно облегчает его решение. Пример 10: ОДЗ: Проверка показывает, что только x=1 является корнем. Ответ: Пример 11:
Тогда Ответ: корней нет. § Область значений функции Пример 12: Данное уравнение не имеет решений, так как его левая часть- функция Ответ: корней нет Пример 13: Учитывая то, что левая часть уравнения – функция
Ответ: корней нет § Свойство ограниченности функции (метод оценок) · Если Пример 14: Заметим, что
Ответ: § Свойство монотонности · Пусть · Пусть Пример 15: . Рассмотрим функции
Значение корня легко найти подбором: Ответ: Пример 16: Функция Ответ: § Использование суперпозиций функций · Если Пример 17: Запишем уравнение в виде Рассмотрим функцию Сделаем замену
Ответ:
Решение уравнений в группах по 6 человек. Ребята получают карточку с заданием. Решение уравнений обсуждают вместе, записывают его.
1 6 5
Учащиеся групп обсуждают решение, исправляют ошибки и выставляют оценки. Потом работы с выставленными оценками возвращаются в группы для обсуждения вклада каждого в решение проблемы. Выставляются каждому оценки с занесением в оценочную таблицу. Учитель контролирует и вносит, если нужно, свои коррективы.
Решить уравнения: 1) 2) 3) 4) 5) 6) 7) 8) *
Используемая литература. 1. Чулков П.В. Материалы курса «Уравнения и неравенства в школьном курсе математики»: Лекции 1-8. – М.: Педагогический университет «Первое сентября», 2006. 2. Дьячков А.К., Иконникова Н.И., Казак В.М., Морозова Е.В. Единый государственный экзамен. Математика. – Челябинск: Взгляд, 2006 –Ч.1,2 3. Шарыгин И. Ф. Факультативный курс по математике: Решение задач. – М.: Просвещение, 1989 4. Черкасов О.Ю., Якушев А.Г. Математика: интенсивный курс подготовки к экзамену. – М.: Айрис-пресс, 2004. 5. Ершова А.П., Голобородько В.В. Самостоятельные и контрольные работы по алгебре и началам анализа для 10-11 классов. – М.: Илекса, 2006.
Задания для работы в группах: Вариант 1(1,3,5 группы). Решите уравнения, используя подсказку: 1. Возведи обе части в квадрат:
2. Выполни замену:
3. Найди ОДЗ:
4. Умножай на сопряжённое выражение:
5. Переходи к модулю:
6. Используй свойства функций:
7. Реши любым способом:
Вариант 2( 2,4,6 группы) Решите уравнения, используя подсказку: 1. Возведи обе части в квадрат:
2. Выполни замену:
3. Найди ОДЗ:
4. Умножай на сопряжённое выражение:
5. Переходи к модулю:
6. Используй свойства функций:
7. Реши любым способом:
Проверочная работа по теме: «Методы Вариант 1
Решите уравнения, используя подсказку: 1. Возведи обе части в квадрат:
2. Выполни замену:
3. Найди ОДЗ:
4. Разложи на множители:
5. Умножай на сопряжённое выражение:
6. Переходи к модулю:
7. Используй свойства функций:
8. Реши любым способом:
решения иррациональных уравнений» Вариант 2
Решите уравнения, используя подсказку: 1. Возведи обе части в квадрат:
2. Выполни замену:
3. Найди ОДЗ:
4. Разложи на множители:
5. Умножай на сопряжённое выражение:
6. Переходи к модулю:
7. Используй свойства функций:
8. Реши любым способом:

12 Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
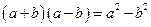
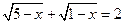






 , то
, то  , тогда
, тогда 
 тогда
тогда 
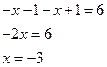
 , тогда
, тогда  ,а
,а 
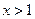 , тогда
, тогда 
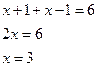


 ОДЗ: x=0 и x=1
ОДЗ: x=0 и x=1
 , тогда
, тогда 
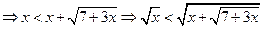

 может принимать только неотрицательные значения.
может принимать только неотрицательные значения.
 может принимать только неотрицательные значения, решим неравенство:
может принимать только неотрицательные значения, решим неравенство: 
 неравенство решений не имеет, тогда и исходное уравнение тоже.
неравенство решений не имеет, тогда и исходное уравнение тоже.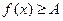 и
и  , то
, то 

 , т.е.
, т.е.  , а
, а 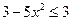

 Проверка показывает, что это значение является и корнем второго уравнения.
Проверка показывает, что это значение является и корнем второго уравнения.
 - функция, возрастающая (убывающая) на некотором промежутке I. Тогда уравнение
- функция, возрастающая (убывающая) на некотором промежутке I. Тогда уравнение  имеет на промежутке I не более одного корня.
имеет на промежутке I не более одного корня. - убывающая на этом промежутке. Тогда уравнение
- убывающая на этом промежутке. Тогда уравнение  имеет на промежутке I. не более одного корня
имеет на промежутке I. не более одного корня
 и
и 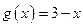 .
.
 возрастает на своей области определения, как сумма двух возрастающих функций, следовательно, уравнение
возрастает на своей области определения, как сумма двух возрастающих функций, следовательно, уравнение  имеет не более одного корня. Так как
имеет не более одного корня. Так как 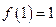 , то
, то 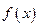 - монотонно возрастающая функция, то уравнения
- монотонно возрастающая функция, то уравнения  и
и  равносильны.
равносильны.

 - монотонно возрастающую, тогда уравнение имеет вид
- монотонно возрастающую, тогда уравнение имеет вид 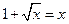

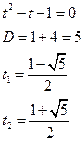 не удовлетворяет условию
не удовлетворяет условию 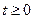





 После выполнения группами заданий проводится взаимопроверка. Группы меняются заданиями с решениями по кругу:
После выполнения группами заданий проводится взаимопроверка. Группы меняются заданиями с решениями по кругу:
 2 3 4
2 3 4