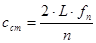|
|
Измерение скорости распространения продольных волн в стержне.12 Цель работы Исследование явления акустического резонанса. Измерение скорости распространения продольных колебаний в тонких стрежнях. Измерение модуля Юнга различных материалов.
В работе используются: генератор звуковых частот, частотомер, осциллограф, электромагнитные излучатель и приемник акустических колебаний, набор образцов в виде стержней и «толстых» цилиндров из различных материалов (стали, алюминия, латуни, текстолита и т. д.).
Распространение продольных волн в тонких стержнях. Акустические волны, распространяющиеся в металлических стержнях, существенно отличаются от волн распространяющихся в неограниченной среде. При этом речь идет о волнах, длина которых λ велика или сравнима с радиусом R стержня. Строгий анализ распространения таких волн связан с довольно громоздкими и трудными математическими расчетами. Рассмотрим распространение продольной волны вдоль оси тонкого стержня постоянного сечения площадью S в пределе. Стержень считается тонким в том случае, когда радиус стержня R мал по сравнению с длиной волны λ, т.е.
Под действием продольной силы F элементарный отрезок стержня Δx, ограниченный плоскостями Δx и x + Δx , растянется или сожмется на величину Δξ . Относительное удлинение, т.е. деформация элемента стержня, будет равна ∂ξ/∂x . Напряжение σ*, т.е. сила, приходящаяся на единицу поперечного сечения стержня, согласно закону Гука, будет равна: (3) Коэффициент пропорциональности Е носит название модуля Юнга и имеет размерность Н/м2. В результате переменной деформации вдоль оси стержня будет распространяться продольная волна. Действительно, в сечениях x и x + Δx напряжения будут различными, а их разность можно записать следующим образом: (4) Эта разность напряжений вызовет движение элемента стержня массой m = SρΔx вдоль оси x . Уравнение движения этого элемента можно записать в виде: (5) где ρ - плотность материала стержня. Обозначив Ε/ρ через (сст)2, выражение (5) запишем в следующем виде: (6) Это уравнение носит название «волнового уравнения». Оно, в частности, описывает распространение продольных волн в стержне. Решение волнового уравнения можно представить в форме двух бегущих волн, распространяющихся в обе стороны вдоль оси x со скоростью Сст: (7) где f и F- произвольные функции. В случае гармонического возбуждения колебаний функции f и g являются синусоидальными Таким образом скорость распространения продольной волны в пределе (8) называемой стержневой скоростью. В данной работе используется именно эта мода. Отметим, что в высокочастотном пределе, когда ( 9 ) где, µ - коэффициент Пуассона. Измерение скорости распространения продольных волн в стержне. Зная плотность материала и величину скорости Сст можно по формуле (8) вычислить модуль Юнга материала Е. Для определения величины скорости Сст в данной работе используется метод акустического резонанса. Это явление состоит в том, что при определенных частотах гармонического возбуждения колебаний волны, распространяющиеся по стержню в противоположные стороны, оказываются в фазе, что приводит к резкому увеличению амплитуды колебаний. В данной работе возбуждение колебаний происходит посредством воздействия на торец стержня периодической силой, направленной вдоль его оси. Возбуждаемая при этом волна испытывает многократные отражения от торцов стержня. При этом прямая и отраженная волны оказываются в фазе и усиливают друг друга, если на длине стержня укладывается целое число полуволн, т.е. (10) Таким образом, для того, чтобы измерить скорость сст, нужно измерить частоты, на которых наблюдаются акустические резонансы и, зная номера гармоник и геометрические размеры стержня, рассчитать скорость по формуле (10). Далее, по формуле (8) можно рассчитать и модуль Юнга материала, из которого изготовлен стержень. Отметим, что такой метод определения модуль Юнга материала является одним из самых точных.

12 Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
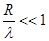 . Направим ось x вдоль геометрической оси стержня (рис. 1).
. Направим ось x вдоль геометрической оси стержня (рис. 1).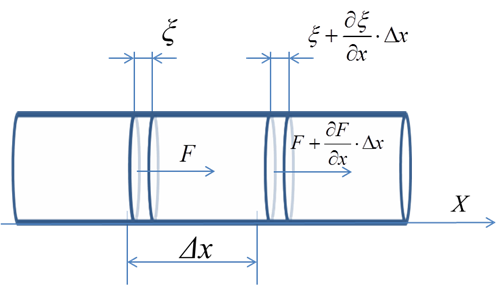
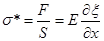
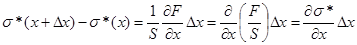
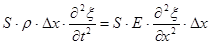 ,
,
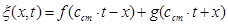

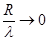 стремится к величине
стремится к величине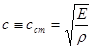
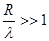 скорость акустических волн в стержне стремится к скорости продольных волн в неограниченной среде:
скорость акустических волн в стержне стремится к скорости продольных волн в неограниченной среде: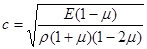
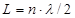 , где L – длина стержня, λ – длина волны, а n – произвольное натуральное число. Число n называют номером гармоники. Зная частоту fn, на которой наблюдается резонансное усиление амплитуды колебаний, вызванных периодическим воздействием на торец стержня и номер гармоники можно рассчитать скорость распространения продольных волн в стержне:
, где L – длина стержня, λ – длина волны, а n – произвольное натуральное число. Число n называют номером гармоники. Зная частоту fn, на которой наблюдается резонансное усиление амплитуды колебаний, вызванных периодическим воздействием на торец стержня и номер гармоники можно рассчитать скорость распространения продольных волн в стержне: