
|
|
Порядок выполнения работы
1. Перенести из табл. 9 лабораторной работы № 6 (см. Приложение) данные канала переменного сечения: значения площадей сечений II и III (внезапное сужение) и полных напоров в этих сечениях; значения площадей сечений IV и V (внезапное расширение) и полных напоров в этих сечениях, а также скоростных напоров в сечениях III и IV (при этом 2. Определить опытные значения местных потерь при внезапном сужении потока 3. Определить опытные значения местных потерь при внезапном расширении потока 4. Найти расчетные значения местных потерь при внезапном сужении 5. Определить относительное расхождение d опытного и расчетного значений потерь напора при внезапном сужении и расширении русла. 6. Сделать выводы по лабораторной работе. Работа 8. ОПРЕДЕЛЕНИЕ потерь напора по длине Цель работы 1. Освоение экспериментального и расчетного методов определения потерь напора на трение по длине. 2. Проведение сравнительного анализа потерь напора по длине, полученных экспериментальным методом, с потерями напора, рассчитанными по формуле Дарси-Вейсбаха при использовании расчетных зависимостей для коэффициента гидравлического трения. Вычисление относительного расхождения экспериментального и расчетного значений потерь напора по длине. Общие сведения В случае установившегося движения жидкости при равномерном её течении эпюра скорости в поперечном сечении не изменяется вдоль потока. Возникающие при этом потери энергии на прямых участках трубопроводов и каналов с постоянными по длине сечениями называются потерями по длине, а гидравлическое сопротивление, вызывающее эти потери, – сопротивлением по длине. Таким образом, сопротивлением по длине называется сопротивление прямых участков трубопроводов и каналов с постоянными по длине сечениями при равномерном движении жидкости. Потери по длине обусловлены внутренним трением в жидкости, поэтому имеют место не только в шероховатых, но и в гладких трубах и каналах. Физической причиной гидравлического трения является вязкость и инерционность жидкости. Таким образом, потери по длине обусловлены инерционно-вязкостными свойствами жидкости и шероховатостью стенок каналов и могут быть определены по формуле Дарси – Вейсбаха:
где Коэффициент сопротивления трения
Здесь l – коэффициент гидравлического трения, который зависит от числа Рейнольдса Re и относительной шероховатости стенок трубы или канала k, то есть
Число Рейнольдса для круглых труб и каналов
для каналов и труб произвольного сечения
здесь Относительная шероховатость k представляет собой отношение абсолютной эквивалентной шероховатости Δ к диаметру d, то есть k = Δ/d. (7) По числу Рейнольдса вся область сопротивления разбита на пять зон. I зона (Re ≤ 2000) – зона ламинарного режима течения. При ламинарном движении коэффициент гидравлического трения l практически не зависит от шероховатости, являясь функцией только числа Рейнольдса, то есть l I = f(Re), и определяется формулой Пуазейля:
II зона (2000<Re<4000) – зона перемежаемости ламинарного и турбулентного режимов течения. При данном режиме течения коэффициент гидравлического трения l также не зависит от шероховатости, а зависит, как и в предыдущем случае, только от числа Рейнольдса, то есть lII = f(Re). С увеличением числа Рейнольдса Re относительная продолжительность существования турбулентного режима растет, ламинарного – уменьшается. В этой зоне коэффициент гидравлического трения
где коэффициент c определяется следующей зависимостью:
III зона В зоне “гладкостенного” сопротивления коэффициент гидравлического трения l зависит только от числа Рейнольдса, то есть Если Re < 105 коэффициент гидравлического трения l может быть определен по формуле Блазиуса:
Если Re > 105 коэффициент гидравлического трения l может быть определен по формуле Филоненко и Альтшуля:
IV зона В этой зоне коэффициент гидравлического трения l зависит как от числа Рейнольдса, так и от шероховатости, то есть
V зона В зоне “квадратичного” сопротивления коэффициент гидравлического трения l вполне определяется шероховатостью стенок канала или труб, то есть
либо формулой Шифринсона
Для определения коэффициента гидравлического трения l в турбулентной области течения можно использовать универсальную формулу Альтшуля:
Рис. 10. График изменения коэффициента гидравлического трения l
Таким образом, объединив зависимости (1) – (3), получим:

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 ) в табл. 10 (см. Приложение).
) в табл. 10 (см. Приложение). как разность полных напоров сечений II и III соответственно.
как разность полных напоров сечений II и III соответственно.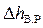 как разность полных напоров сечений IV и V соответственно.
как разность полных напоров сечений IV и V соответственно. и внезапном расширении
и внезапном расширении  потока, используя формулу Вейсбаха (1), также формулы (3) и (4) для определения коэффициентов местных сопротивлений при внезапном сужении и расширении русла соответственно.
потока, используя формулу Вейсбаха (1), также формулы (3) и (4) для определения коэффициентов местных сопротивлений при внезапном сужении и расширении русла соответственно. , (1)
, (1)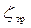 – коэффициент сопротивления трения;
– коэффициент сопротивления трения; 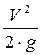 – скоростной напор, рассчитанный по средней скорости V.
– скоростной напор, рассчитанный по средней скорости V. – для круглых труб и каналов, (2)
– для круглых труб и каналов, (2) – для остальных труб. (3)
– для остальных труб. (3)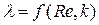 . (4)
. (4) , (5)
, (5)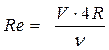 , (6)
, (6)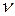 – кинематический коэффициент вязкости, м2/с.
– кинематический коэффициент вязкости, м2/с. (8)
(8)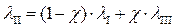 , (9)
, (9)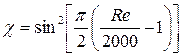 (10)
(10) – зона “гладкостенного” сопротивления.
– зона “гладкостенного” сопротивления.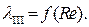
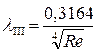 . (11)
. (11) (12)
(12)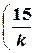 < Re <
< Re <  – переходная зона.
– переходная зона. и может быть определен по формуле Кольбрука:
и может быть определен по формуле Кольбрука: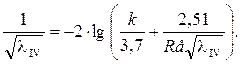 (13)
(13)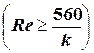 – зона “квадратичного” сопротивления.
– зона “квадратичного” сопротивления.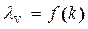 . Для определения коэффициента гидравлического трения l в этой зоне можно, например, воспользоваться формулой Никурадзе и Прандтля:
. Для определения коэффициента гидравлического трения l в этой зоне можно, например, воспользоваться формулой Никурадзе и Прандтля: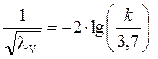 , (14)
, (14) . (15)
. (15)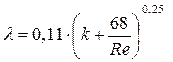 . (16)
. (16)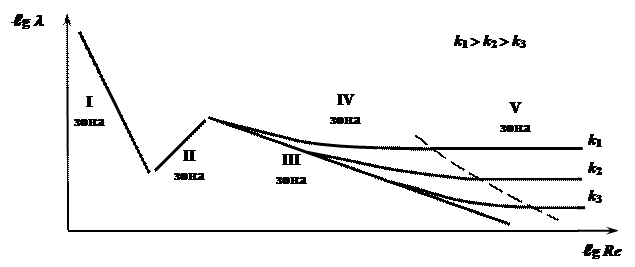 На рис. 10 показана зависимость коэффициента гидравлического трения l от числа Рейнольдса Re во всей области сопротивления.
На рис. 10 показана зависимость коэффициента гидравлического трения l от числа Рейнольдса Re во всей области сопротивления.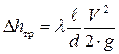 – для круглых труб и каналов, (17)
– для круглых труб и каналов, (17)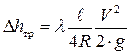 – для труб и каналов любого профиля. (18)
– для труб и каналов любого профиля. (18)