
|
|
Порядок выполнения работы
1. Заполнив водой бак 1 (см. рис. 5), перевернуть устройство для получений течения в канале постоянного сечения 4. 2. Снять показания пьезометров равен нулю, то есть 3. Измерить время t (в секундах) перемещения уровня воды в баке на произвольно заданную величину S. 4. По данным измерений определить: а) расход жидкости
числовые значения поперечного сечения бака А и В определить по табло на устройстве № 4; б) среднюю скорость потока в сечениях I …VI (значения площадей сечений w приведены на табло устройства № 4)
в) скоростные напоры г) полные напоры 5. Данные опытов занести в табл. 9 (см. Приложение). 6. Построить для данного канала пьезометрическую линию. Для этого, обозначив контуры канала, отложить в масштабе от его осевой линии (плоскости сравнения) для сечений I…VI пьезометрические напоры 7. На том же рисунке построить напорную линию. Для этого в масштабе отложить для каждого сечения I …VI от пьезометрической линии скоростные напоры
Рис. 6. Построение напорных линий для канала постоянного сечения
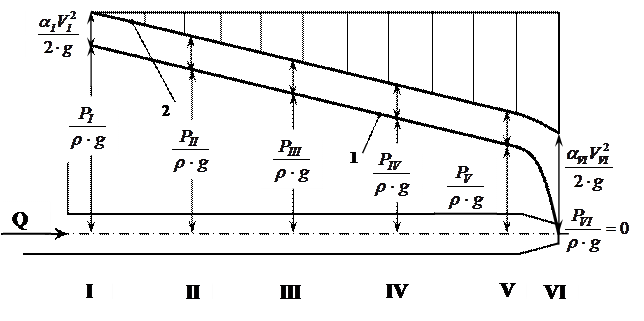
8. Заполнив водой бак 2 (см. рис. 5) и перевернув устройство для получения течения в канале переменного сечения 3, повторить опыт по пп. 2…7. Пьезометрическая и напорная линии для данного канала показаны на рис. 7 кривой 1 и 2 соответственно. 9. Сделать выводы по данной работе.
Рис. 7. Построение напорных линий для канала переменного сечения
Работа 7. Исследование местных гидравлических
Цель работы 1. Освоение методики опытного определения потерь напора в местных гидравлических сопротивлениях. 2. Проведение сравнительного анализа потерь напора в местных сопротивлениях, полученных опытным путем, с потерями напора, рассчитанными по формуле Вейсбаха при использовании инженерных зависимостей для коэффициентов местных сопротивлений. Вычисление относительного расхождения опытного и расчетного значений потерь напора в местных гидравлических сопротивлениях.
Общие сведения Местные изменения размеров или конфигурации русла на различных фасонных участках (внезапное или плавное расширение (сужение), вентили, задвижки, клапаны, колена, арматура и т.п.) вызывают деформацию и изменение скорости потока. При прохождении жидкости через фасонные участки происходит отрыв транзитного потока от стенок русла, образуются циркуляционные зоны, на вращение жидкости в которых затрачивается часть механической энергии потока. Гидравлические сопротивления фасонных участков называются местными сопротивлениями, потери механической энергии в этих местных сопротивлениях называютсяместными потерями энергии. Потери напора в местных гидравлических сопротивлениях с физической точки зрения обусловлены инерционно-вязкостным взаимодействием жидкости со стенками фасонных участков русла и могут быть определены по формуле Вейсбаха:
где z – коэффициент местного сопротивления; V – средняя по сечению скорость, м/с. Если скорость в местном гидравлическом сопротивлении изменяется по длине, то за расчетную скорость принято принимать бóльшую из скоростей. Сложный характер взаимодействия потока жидкости с местными гидравлическими сопротивлениями не позволяет, как правило, установить аналитические зависимости для определения коэффициентов местных сопротивлений z. Для большинства местных сопротивлений коэффициенты z определяются опытным путем. В общем случае, как показывают расчеты и данные опытов, коэффициенты z зависят от геометрии фасонного участка трубы или канала и от состояния потока. При этом влияние числа Рейнольдса Reна коэффициенты многих местных сопротивлений ограничивается, как правило, областью ламинарного течения жидкости. При турбулентном течении коэффициенты местных сопротивлений z определяются в основном формой местных сопротивлений и геометрическими параметрами и не зависят от числа Рейнольдса, что означает квадратичный закон сопротивления или автомодельность. Величина местных потерь напора экспериментально определяется разностью полных напоров жидкости до и после местного сопротивления. При этом коэффициент местного сопротивления z определяется отношением местных потерь напора к скоростному напору, то есть
При расчетномопределении потерь напора по формуле Вейсбаха (1) коэффициент местного сопротивления при внезапном сужении русламожет быть определен по полуэмпирической формуле Идельчика:
При определении потерь напора при внезапном сужении потока Коэффициент местного сопротивления при внезапном расширении русламожет быть определен по следующей аналитической зависимости:
При определении потерь напора при внезапном расширении потока

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 по нижним положениям менисков воды в них для пяти сечений I …V, пьезометрический напор в шестом сечении
по нижним положениям менисков воды в них для пяти сечений I …V, пьезометрический напор в шестом сечении .
. , (5)
, (5) ; (6)
; (6) в сечениях I…VI, приняв коэффициент кинетической энергии aI…a VI »1;
в сечениях I…VI, приняв коэффициент кинетической энергии aI…a VI »1; в сечениях канала I…VI, совместив плоскость сравнения с осевой линией потока (таким образом,
в сечениях канала I…VI, совместив плоскость сравнения с осевой линией потока (таким образом,  (или от осевой линии потока – полные напоры
(или от осевой линии потока – полные напоры  ) и соединить полученные точки (см. рис. 6, кривая 2).
) и соединить полученные точки (см. рис. 6, кривая 2).


 , (1)
, (1)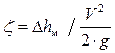 . (2)
. (2)
 . (3)
. (3) необходимо коэффициент
необходимо коэффициент  умножить на бóльший скоростной напор, то есть на V2 /2×g.
умножить на бóльший скоростной напор, то есть на V2 /2×g.
 (4)
(4) необходимо коэффициент
необходимо коэффициент  умножить на бóльший скоростной напор, то есть на V1 /2×g.
умножить на бóльший скоростной напор, то есть на V1 /2×g.