|
|
Уравнение расхода для несжимаемой и сжимаемой жидкостиРассмотрим поток жидкости и предположим, что в сечениях А-А и В-В (рис.1.1) скорости по всему сечению равны средней скорости и направлены параллельно оси горизонтально расположенной трубы. Согласно закону сохранения энергии
для случая несжимаемой жидкости (
где Согласно условию неразрывности струи для несжимаемой жидкости (закон сохранения материи):
Выразим
где Подставив (1.4) и (1.5) в (1.3), получим
Подставим выражение (1.6) в (1.2), после чего выразим скорость в самом узком сечении струи (
Давления
Секундный расход в единицах объема для несжимаемой жидкости может быть выражен как
Коэффициенты
который называют коэффициентом расхода и определяют экспериментальным путем. Уравнения расхода для несжимаемой жидкости приобретают вид:
где Подставив (1.14) в (1.1) и проинтегрировав (1.1) для сечений А-А и В-В, получим
Подставляя на основании (1.13) в уравнение (1.15) значение
получаем
Уравнение неразрывности потока сжимаемой жидкости для сечений
Выразим
где через Подставим (1.18) в (1.17), после чего выразим (1.18) относительно
Подставляя (1.19) в (1.16), находим среднюю скорость в наиболее узком сечении потока
Как и для несжимаемой жидкости, введем коэффициент
Уравнение расхода (1.21) можно представить в виде, аналогичном уравнению для несжимаемой жидкости, что более удобно для практических целей:
где
где
Уравнения (1.22) и (1.23) отличаются от уравнений для несжимаемой жидкости (1.11) и (1.12) только поправочным множителем на расширение измеряемой среды. Поэтому уравнения (1.22) и (1.23) действительны также для несжимаемой жидкости, поскольку для нее поправочный множитель Данные уравнения расхода для сжимаемой жидкости могут применяться только в том случае, когда скорость потока в сужающем устройстве не достигает критической, т.е. скорости звука в данной среде. 11.Уравнение Бернули. Физический смысл и примеры приминения Закон (уравнение) Бернулли является (в простейших случаях[1][2][3][4]) следствием закона сохранения энергии для стационарного потока идеальной (то есть без внутреннего трения) несжимаемой жидкости:
Здесь
Уравнение Бернулли также может быть выведено как следствие уравнения Эйлера, выражающего баланс импульса для движущейся жидкости[5]. В научной литературе закон Бернулли, как правило, называется уравнением Бернулли[6](не следует путать сдифференциальным уравнением Бернулли), теоремой Бернулли[7][8] или интегралом Бернулли[5][9]. Константа в правой части часто называется полным давлением и зависит, в общем случае, от линии тока. Размерность всех слагаемых — единица энергии, приходящаяся на единицу объёма жидкости. Первое и второе слагаемое в интеграле Бернулли имеют смысл кинетической и потенциальной энергии, приходящейся на единицу объёма жидкости. Следует обратить внимание на то, что третье слагаемое по своему происхождению являетсяработой сил давления (см. приводимый в приложении вывод уравнения Бернулли) и не представляет собой запаса какого-либо специального вида энергии («энергии давления»[10]). Соотношение, близкое[11] к приведенному выше, было получено в 1738 г. Даниилом Бернулли, с именем которого обычно связывают интеграл Бернулли. В современном виде интеграл был получен Иоганном Бернулли около 1740 года. Для горизонтальной трубы высота Эта форма уравнения Бернулли может быть получена путём интегрирования уравнения Эйлера для стационарного одномерного потока жидкости, при постоянной плотности
Согласно закону Бернулли, полное давление в установившемся потоке жидкости остается постоянным вдоль этого потока. Полное давление состоит из весового Из закона Бернулли следует, что при уменьшении сечения потока, из-за возрастания скорости, то есть динамического давления, статическое давление падает. Это является основной причиной эффекта Магнуса. Закон Бернулли справедлив и для ламинарных потоков газа. Явление понижения давления при увеличении скорости потока лежит в основе работы различного родарасходомеров (например труба Вентури), водо- и пароструйных насосов. А последовательное применение закона Бернулли привело к появлению технической гидромеханической дисциплины — гидравлики. Закон Бернулли справедлив в чистом виде только для жидкостей, вязкость которых равна нулю. Для приближённого описания течений реальных жидкостей в технической гидромеханике (гидравлике) используют интеграл Бернулли с добавлением слагаемых, учитывающих потери на местных и распределенных сопротивлениях. Известны обобщения интеграла Бернулли для некоторых классов течений вязкой жидкости (например, для плоскопараллельных течений[12]), в магнитной гидродинамике[13], феррогидродинамике[14]. Одно из применений[править | править вики-текст] Закон Бернулли можно применить к истечению идеальной несжимаемой жидкости через малое отверстие в боковой стенке или дне широкого сосуда.
Закон Бернулли позволяет объяснить эффект Вентури: в узкой части трубы скорость течения жидкости выше, а давление меньше, чем на участке трубы большего диаметра, в результате чего наблюдается разница высот столбов жидкости Согласно закону Бернулли приравняем полные давления на верхней поверхности жидкости и на выходе из отверстия:
где
Отсюда: Часто уравнение Бернулли записывается в виде:
где
Для сжимаемого идеального газа[править | править вики-текст]
где
При движении в неоднородном поле
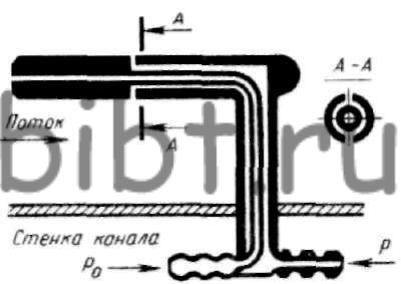
12. Измерение давления, скорости и расхода жидкостиПИТО-ПРАНДТЛЯ ТРУБКА - устройство для измерения давления, а также направления потока жидкости или газа и их расхода, основанное на измерении давления в потоке. Пито-прандтля трубку устанавливают вдоль потока (рис. П-17). Через центральное отверстие измеряют полное давление р0; через боковые - статическое давление р. Скорость потока вычисляют по формуле
Рис. П-17. Схема трубки Пито-Прандтля 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
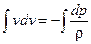 (1.1)
(1.1) ), получим
), получим , (1.2)
, (1.2)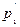 и
и  – абсолютные давления в сечениях А-А и В-В соответственно, Па;
– абсолютные давления в сечениях А-А и В-В соответственно, Па; 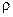 – плотность протекающей жидкости перед сужающим устройством, кг/м3;
– плотность протекающей жидкости перед сужающим устройством, кг/м3; 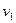 и
и 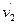 – средние скорости потока жидкости в сечениях А-А и В-В соответственно, м/с.
– средние скорости потока жидкости в сечениях А-А и В-В соответственно, м/с. . (1.3)
. (1.3) и
и 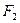 через
через 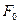 – площадь отверстия сужающего устройства при рабочей температуре, м2 :
– площадь отверстия сужающего устройства при рабочей температуре, м2 :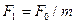 , (1.4)
, (1.4)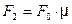 , (1.5)
, (1.5)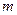 – относительная площадь сужающего устройства (
– относительная площадь сужающего устройства (  , здесь
, здесь  и
и 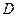 – соответственно диаметр отверстия сужающего устройства и трубопровода при рабочей температуре);
– соответственно диаметр отверстия сужающего устройства и трубопровода при рабочей температуре); 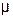 – коэффициент сужения струи.
– коэффициент сужения струи. . (1.6)
. (1.6)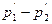 ):
): . (1.7)
. (1.7) и
и  и
и 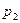 (рис. 1.1) в формулу (1.7) вводят поправочный коэффициент
(рис. 1.1) в формулу (1.7) вводят поправочный коэффициент  и уравнение средней скорости в наиболее узком сечении потока принимает вид
и уравнение средней скорости в наиболее узком сечении потока принимает вид . (1.8)
. (1.8)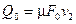 или
или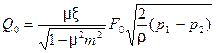 . (1.9)
. (1.9) не могут быть определены с достаточной точностью независимо друг от друга. Поэтому их объединяют в один общий коэффициент
не могут быть определены с достаточной точностью независимо друг от друга. Поэтому их объединяют в один общий коэффициент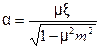 , (1.10)
, (1.10)
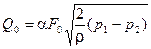 ; (1.11)
; (1.11)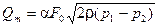 , (1.12)
, (1.12)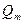 – расход в единицах массы, кг/с.
– расход в единицах массы, кг/с.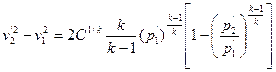 . (1.15)
. (1.15) ,
, . (1.16)
. (1.16) . (1.17)
. (1.17)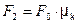 , (1.18)
, (1.18) обозначен коэффициент сужения, который отличается от коэффициента сужения для несжимаемой жидкости, так как он зависит от отношения давлений
обозначен коэффициент сужения, который отличается от коэффициента сужения для несжимаемой жидкости, так как он зависит от отношения давлений 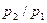 . Это происходит потому, что вследствие отсутствия боковых стенок, особенно у диафрагм, газ или перегретый пар может расширяться в радиальном направлении. Следовательно, наименьшее сечение струи потока для сжимаемой жидкости за диафрагмой будет несколько больше, чем для несжимаемой жидкости, так как сжимаемая жидкость будет несколько увеличиваться в объеме вследствие уменьшения давления за сужающим устройством.
. Это происходит потому, что вследствие отсутствия боковых стенок, особенно у диафрагм, газ или перегретый пар может расширяться в радиальном направлении. Следовательно, наименьшее сечение струи потока для сжимаемой жидкости за диафрагмой будет несколько больше, чем для несжимаемой жидкости, так как сжимаемая жидкость будет несколько увеличиваться в объеме вследствие уменьшения давления за сужающим устройством.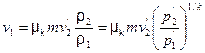 . (1.19)
. (1.19)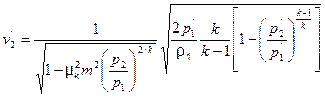 . (1.20)
. (1.20)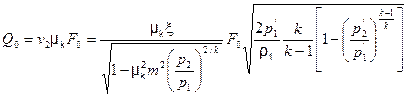 . (1.21)
. (1.21) ; (1.22)
; (1.22) , (1.23)
, (1.23)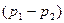 – перепад давления на сужающем устройстве, Па;
– перепад давления на сужающем устройстве, Па; 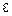 – поправочный множитель на расширение измеряемой среды, равный
– поправочный множитель на расширение измеряемой среды, равный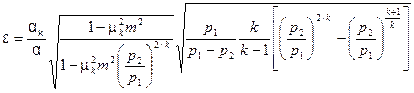 , (1.24)
, (1.24)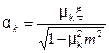 . (1.25)
. (1.25)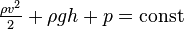
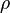 — плотность жидкости,
— плотность жидкости, — скорость потока,
— скорость потока,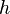 — высота, на которой находится рассматриваемый элемент жидкости,
— высота, на которой находится рассматриваемый элемент жидкости,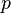 — давление в точке пространства, где расположен центр массы рассматриваемого элемента жидкости,
— давление в точке пространства, где расположен центр массы рассматриваемого элемента жидкости,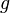 — ускорение свободного падения.
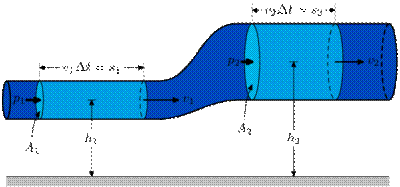
— ускорение свободного падения.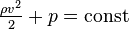 .
. .
.
 , статического
, статического 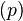 и динамического
и динамического 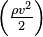 давлений.
давлений.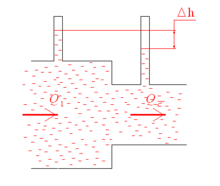
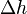 ; бо́льшая часть этого перепада давлений обусловлена изменением скорости течения жидкости, и может быть вычислена по уравнению Бернулли
; бо́льшая часть этого перепада давлений обусловлена изменением скорости течения жидкости, и может быть вычислена по уравнению Бернулли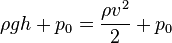 ,
, — атмосферное давление,
— атмосферное давление,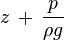 — гидростатический напор (сумма геометрического напора z и пьезометрической высоты
— гидростатический напор (сумма геометрического напора z и пьезометрической высоты 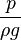 ).
).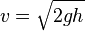 . Это — формула Торричелли. Она показывает, что при истечении идеальной несжимаемой жидкости из отверстия в широком сосуде жидкость на выходе приобретает скорость, какую получило бы тело, свободно падающее с высоты
. Это — формула Торричелли. Она показывает, что при истечении идеальной несжимаемой жидкости из отверстия в широком сосуде жидкость на выходе приобретает скорость, какую получило бы тело, свободно падающее с высоты 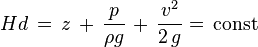
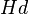 — гидродинамический напор,
— гидродинамический напор, — скоростной напор.
— скоростной напор.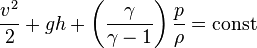 [15] (постоянна вдоль линии тока или линии вихря)
[15] (постоянна вдоль линии тока или линии вихря)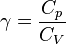 — Адиабатическая постоянная газа
— Адиабатическая постоянная газа — давление газа в точке
— давление газа в точке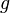 — ускорение свободного падения
— ускорение свободного падения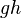 заменяется на потенциал гравитационного поля.
заменяется на потенциал гравитационного поля.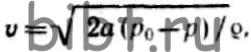 где а - поправочный коэф.; ρ- плотность газа или жидкости.
где а - поправочный коэф.; ρ- плотность газа или жидкости.