
|
|
Обработка ряда равноточных измерений одной величины
Порядок обработки результатов рядаравноточных измерений одной величины следующий. 1. Вычислить среднее арифметическое хо по формуле (3.7). 2. Получить ряд уклонений результатов измерений от среднего арифметического по формуле (3.8). 3. Проконтролировать сумму уклонений. Сумма уклонений от среднего арифметического должна быть равна нулю в пределах погрешностей округлений, т.е. [v] = 0. В значении среднего арифметического для начальной обработки следует оставлять после запятой на один знак больше, чем в результатах измерений. При этом, из-за возможного округления среднего арифметического, сумма уклонений может незначительно отличаться от нуля. 4. Составить ряд квадратов уклонений v2 и получить сумму квадратов уклонений [v2]. 5. Вычислить СКП одного измерения по формуле (3.10). 6. Вычислить СКП СКП по формуле (3.11); 7. Вычислить СКП среднего арифметического по формулам (3.21) или (3.22). 8. Вычислить относительную погрешность результата измерения по формуле (3.2), используя в числителе значение СКП результата измерения. 9. Вычислить относительную погрешность среднего арифметического по формуле (3.2), используя в числителе значение СКП среднего арифметического. 10. Произвести округление результатов в соответствии со значением СКП среднего арифметического и записать окончательное значение измеренной величины с её доверительным интервалом (для заданной доверительной вероятности). В табл. 3.2 приведен пример обработки результатов измерений линии, измеренной на местности рулеткой с миллиметровыми делениями.
Пример 3.5. Обработка ряда равноточных измерений одной величины Решение. СКП одного измерения (формула Бесселя): m = 0,004645 м. СКП средней квадратической ошибки одного измерения (3.11): mm= 0,000519 м. СКП среднего арифметического, (3.21) или (3.22): М = 0,00073 м. Таблица 3.2 К примеру 3.5
хо = 83,6619 [v] = 0 [v2] =841,60∙10-6
На основании значения mm величину m можно округлить до m = 0,005 м. Значение среднего арифметического округлять здесь не следует, поскольку разряд округления и значение погрешнсоти среднего арифметического (М = 0,0007 м) – одного порядка. С учетом данных табл. 3.1 можно записать значение измеренной величины в виде доверительного интервала ±tM с заданной вероятностью Р: Х(Р=68,3%) = (83,6619 ± 0,0007) м; Х(Р=95,5%) = (83,6619 ± 0,0014) м; Х(Р=99,7%) = (83,6619 ± 0,0021) м. Запись, например, для Х(Р=95,5%) расшифровывается так: с вероятностью 95,5% величина Х находится в интервале 83,6605 м < Х < 83,6633 м . Проконтролируем ряд значений хi, приведённый в табл. 3.2, на соответствие его нормальному закону распределения. Найдём для этого число измерений, для которых их погрешности находятся в пределах ±m, ±2m и ±3m, т.е. в пределах (83,662±0,005) м, (83,662±0,010) м и (83,662±0,015) м, с округлением среднего арифметического и СКП одного измерения до 0,001 м (как было получено при измерениях). Получим: n(t = 1) = 28, n(t = 2) = 40, n(t = 3) – нет. Отношение n(t = 1) к общему числу измерений n = 40 равно 70%, что примерно соответствует вероятности Р = 68,3% для нормального закона распределения. Отклонение объясняется ограниченным числом измерений.
Рассмотрим ещё один пример на обработку результатов измерений с использованием формул (3.12), (3.13) и (3.14).
Пример 3.6.Оценка СКП по значениям вероятной и средней погрешностей. Исходные данные см. табл. 3.2. Таблица 3.3 К примеру 3.6
Решение. Расположим ряд случайных погрешностей, полученный в таблице по их возрастанию по абсолютной величине (без учета знака погрешности) – табл. 3.3. Середина ряда соответствует порядковым номерам 20 и 21, т.е. срединная погрешность равна r = 3,1 мм. Из формулы (3.12) следует, что m = r/0,67 = 4,627 мм (в примере 3.5 m = 4,645 мм). Получим среднюю погрешность. Сумма абсолютных погрешостей Как видим, отклонения значений СКП, полученной ранее в примере 3.5, от значений, полученных через срединную и среднюю погрешности, являются вполне приемлемыми. Однако не следует стремиться упрощать подобные оценки (вычисления). Дело в том, что в примерах рассмотрен довольно большой по объёму ряд случайных погрешностей. На практике же обычно ряды случайных погрешностей по объёму меньше, поэтому и не следует ожидать таких близких результатов, даже если этот небольшой ряд и подчиняется нормальному закону распределения. В связи с этим целесообразно, всё-таки, вычисления выполнять по схеме, представленной в примере 3.5. Часто обработку ряда случайных погрешностей выполняют по несколько другой схеме, более простой. Для этого в ряду измеренных величин выбирают самое маленькое значение xmin и образуют ряд уклонений
в котором все значения уклонений Далее сумму квадратов уклонений результатов измерений от среднего арифметического определяют по формуле
а значение среднего арифметического определяют по формуле
Дальнейшие расчеты аналогичны приведенным в примере 3.4. Рассмотрим решение задачи, приведенной в примере 3.5, с использованием данной схемы. Пример 3.7.Обработка ряда равноточных измерений через уклонения Решение. Таблица 3.4 К примеру 3.7
По формуле (3.30) находим По формуле (3.31) находим значение среднего арифметического
Далее все вычисления повторяют аналогичные расчёты, выполненные в примере 3.5. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
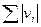 = 146,6 мм. По формуле (3.14) находим vo = 3,665. По формуле (3.15) находим m = 1,25∙3,665 = 4,581 мм (в примере 3.5 m = 4,645 мм).
= 146,6 мм. По формуле (3.14) находим vo = 3,665. По формуле (3.15) находим m = 1,25∙3,665 = 4,581 мм (в примере 3.5 m = 4,645 мм). , (3.29)
, (3.29) будут положительными.
будут положительными. , (3.30)
, (3.30)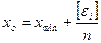 . (3.31)
. (3.31) ;
;  .
. мм2 = 841,6∙10-6 м2 (такой же точно результат, как и в примере 3.5).
мм2 = 841,6∙10-6 м2 (такой же точно результат, как и в примере 3.5).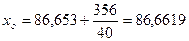 м (такой же результат, как и в примере 3.5).
м (такой же результат, как и в примере 3.5).