
|
|
Формулы логики предикатов
81. Пусть F1 и F2 являются формулами логики предикатов. Какое из приведенных ниже выражений не является формулой. а) F1F2. б) в) г)
82. Пусть F1 и F2 являются формулами логики предикатов. Какое из приведенных ниже выражений не является формулой. а) б) в) г)
83. Формула логики предикатов называется выполнимой на множестве М, если при некоторой подстановке вместо предикатных переменных конкретных предикатов, заданных на этом множестве, она превращается в а) опровержимый предикат. б) выполнимый предикат. в) тождественно истинный предикат. г) тождественно ложный предикат.
84: Формула логики предикатов называется опровержимой) на множестве М, если при некоторой подстановке вместо предикатных переменных конкретных предикатов, заданных на этом множестве, она превращается в а) опровержимый предикат. б) выполнимый предикат. в) тождественно ложной предикат. г) тождественно истинный предикат.
85. Формула логики предикатов называется тождественно истиннойна множестве М, если при всякой подстановке вместо предикатных переменных любых конкретных предикатов, заданных на этом множестве, она превращается в. : а) опровержимый предикат. б) выполнимый предикат. в) тождественно истинный предикат. г) тождественно ложный предикат.
86: Формула логики предикатов называется тождественно ложной на множестве М, если при всякой подстановке вместо предикатных переменных любых конкретных предикатов, заданных на этом множестве, она превращается в а) опровержимый предикат. б) выполнимый предикат. в) тождественно истинный предикат. г) тождественно ложный предикат.
87. Формула логики предикатов называется общезначимой, или тавтологией, если при всякой подстановке вместо предикатных переменных любых конкретных предикатов, заданных на каких угодно множествах, она превращается в а) опровержимый предикат. б) выполнимый предикат. в) тождественно истинный предикат. г) тождественно ложный предикат.
88. Формула логики предикатов называется тождественно ложной или противоречием, если при всякой подстановке вместо предикатных переменных любых конкретных предикатов, заданных на каких угодно множествах, она превращается в а) опровержимый предикат. б) выполнимый предикат. в) тождественно истинный предикат. г) тождественно ложный предикат.
89. Каким из ниже перечисленных слов или сочетанием слов следует заменить символ Всякая формула, получающаяся из тавтологии алгебры высказываний заменой входящих в нее пропозициональных переменных произвольными а) пропозициональными переменными. б) кванторными переменными. в) предметными переменными. г) предикатными переменными.
90. Каким из ниже перечисленных символов следует заменить символ
а) б) в) г)
91. Каким из ниже перечисленных символов следует заменить символ
а) б) в) г)
92. Каким из ниже перечисленных символов следует заменить символ
а) б) в) г)
93. Каким из ниже перечисленных символов следует заменить символ
а) б) в) г)
94. Две формулы, F и H, логики предикатов называются равносильными на множестве М,если при любой подстановке в эти формулы вместо предикатных переменных любых конкретных предикатов, определенных на М, формулы превращаются в а) одноместные предикаты б) равносильные предикаты. в) опровержимые предикаты г) выполнимые предикаты
95. Приведенной формойдля формулы логики предикатов называется такая равносильная ей формула, в которой из операций алгебры высказываний имеются только операции а) кванторам. б) высказываниям. в) предметным переменным. г) к тавтологиям.
96 Предваренной нормальной формойдля формулы логики предикатов называется такая ее приведенная форма, в которой все кванторы стоят в ее начале, а область действия каждого из них распространяется до конца формулы, то есть это формула вида а) тавтологией. б) высказыванием. в) приведенной формой. г) предикатом.
97. Резольвентой для родительских предложений P и ØPÚQ является а) Q б) P в) ØP г) NIL
98. Резольвентой для родительских предложений PÚQ и ØPÚQ является а) Q б) P в) ØP г) NIL
99. Резольвентой для родительских предложений ØPÚQ и ØQÚR является а) Q б) ØPÚR в) ØPÚQ г) NIL
100. Одной из возможных резольвент для родительских предложений PÚQ и ØPÚØQ является а) Q б) QÚØQ в) ØPÚQ г) NIL Раздел 6. Теория алгоритмов.
101. Каким из ниже перечисленных слов следует заменить символ Функция f(x1, . . ., хп) называется а) разрешимой. б) перечислимой. в) вычислимой г) аналитической.
102. Каким из ниже перечисленных слов следует заменить символ Множество М называется а) разрешимым. б) перечислимым. в) вычислимым г) аналитическим.
103. Каким из ниже перечисленных слов следует заменить символ Множество M, являющееся подмножеством натуральных чисел, называется а) разрешимым. б) перечислимым. в) вычислимым г) аналитическим.
104. Применение к слову 138578926 Марковской подстановки (85789, 00) дает результат: а) 138578 б) 130026 в) 8578926 г) 0085789
105 Применение к слову шрам Марковской подстановки (ра, ар) дает результат:
а) шарш б) марш в) шарм г) рашм
106. Каким из ниже перечисленных слов следует заменить символ Упорядоченный конечный список формул подстановок в алфавите А:
называется а) схемой б) программой в) функцией г) командой
107. Пусть А={ a0, a1, a2,….., an, } –алфавит. Рассмотрим схему нормального алгоритма
В какое слово она перерабатывает слово ana0a1a2 ? а) a1a2 б) a0a1a2 в)
108.Завершите формулировку принципа нормализации Маркова: Для нахождения значений функции, заданной в некотором алфавите, тогда и только тогда существует какой-нибудь алгоритм, когда функция нормально а) разрешима б) перечислима в) определена г) вычислима
109. Дана система команд машины Тьюринга: q1a1→q2λR; q1a2→q3λR; q2a2→q3λR; q3a2→q1λR; q3a1→q4TE; и лента с записью: а1 а2 а2 а1 а1; начальное состояние: q1. Данная машина: а)сотрёт всю ленту; б)оставит на ленте символ а1; в)оставит на ленте символ Т; г)зациклится.
110. Рассмотрим машину Тьюринга с алфавитом
Какую операцию в унарном коде выполняет эта машина. а) копирование. б) сложение двух натуральных чисел. в) умножение двух натуральных чисел. г) стирание всех слов с ленты.
111. Рассмотрим машину Тьюринга с алфавитом
Какую операцию в унарном коде выполняет эта машина. а) копирование. б) сложение двух натуральных чисел. в) умножение двух натуральных чисел. г) стирание всех слов с ленты.
112. В теории рекурсивных функций в качестве набора операторов, с помощью которых строятся новые функции, выбраны следующие наборы: Варианты ответов а) оператор проектирования, оператор суперпозиции; б) оператор проектирования, оператор минимизации; в) интегральный оператор, оператор суперпозиции, оператор примитивной рекурсии; г) оператор суперпозиции, оператор примитивной рекурсии, оператор минимизации;
113.: Выразить функцию s(x,y)= x + y через простейшие функции с помощью оператора примитивной рекурсии Варианты ответов
a)
114. С помощью ограниченного оператора минимизации, простейшие и примитивно-рекурсивные функции s(x,y)= x + y и p(x,y)= x Варианты ответов а) б) в) г)
115. Завершите формулировку тезиса Черча: Всякая функция, вычислимая некоторым алгоритмом, а) примитивно-рекурсивна б) рекурсивна. в) разрешима. г) перечислима.
116.Для указанных классов функций, заданных на множестве натуральных чисел и принимающих натуральные значения, справедливо следующее утверждение: а) класс всех функций, вычислимых по Тьюрингу, совпадает с классом всех нормально вычислимых функций, но не совпадает с классом всех рекурсивных функций б) класс всех нормально вычислимых функций совпадает с классом всех рекурсивных функций, но не совпадает классом всех функций, вычислимых по Тьюрингу. в) существует рекурсивная функция, вычислимая по Тьюрингу, но не вычислимая никаким нормальным алгоритмом г) все три класса (класс всех функций, вычислимых по Тьюрингу, класс всех нормально вычислимых функций, класс всех рекурсивных функций) совпадают.
117.: Рассмотрим следующую функцию Для произвольного слова
а) вычислима по Тьюрингу б) не вычислима по Тьюрингу. в) перечислима по Тьюрингу г) примитивно-рекурсивна
118. Проблема распознавания самоприменимых машин Тьюринга алгоритмически . а) вычислима б) разрешима в) неразрешима г) перечислима
119.: а) Класс а) с той же скоростью, как и данная функция f . б) по крайней мере так же быстро, как данная функция f . в) сложность которых растёт медленнее, чем функция f . г) очень быстро.
120. Класс NP содержит задачи, для которых алгоритмы, способные решить их за разумное время а) известны. б) эффективны. в) не известны. г) приводится в справочниках.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
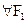





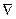 в следующей теореме.
в следующей теореме.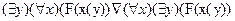 , чтобы получить тавтологию логики предикатов.
, чтобы получить тавтологию логики предикатов.
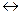


 , чтобы получить тавтологию логики предикатов.
, чтобы получить тавтологию логики предикатов.
 , чтобы получить тавтологию логики предикатов.
, чтобы получить тавтологию логики предикатов. , чтобы получить тавтологию логики предикатов.
, чтобы получить тавтологию логики предикатов. , а знаки отрицания относятся лишь к предикатным переменным и к
, а знаки отрицания относятся лишь к предикатным переменным и к ,где Ki есть один из кванторов
,где Ki есть один из кванторов  ), а формула F не содержит кванторовиявляется
), а формула F не содержит кванторовиявляется

 г) an
г) an и системой команд
и системой команд
 и системой команд
и системой команд
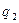


 б)
б)  в)
в) 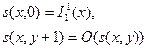 г)
г) 
 y выразите целую часть
y выразите целую часть  .
.


 на словах в алфавите A1 ={1}.
на словах в алфавите A1 ={1}. длины п в алфавите A1 ={1}положим:
длины п в алфавите A1 ={1}положим: Тогда функция
Тогда функция  (f) содержит алгоритмы, сложность которых растёт
(f) содержит алгоритмы, сложность которых растёт