|
|
Формулы алгебры высказываний. Формальное исчисление высказываний
41. Формула алгебры высказываний называется выполнимой, если:
а) она на любом наборе высказываний, подставляемых вместо пропозициональных переменных, представляет собой ложное высказывание б) существует такой набор высказываний, при подстановке которого в формулу получится ложное высказывание в) существует такой конкретный набор высказываний, при подстановке которого в формулу получается истинное высказывание г) при подстановке любых наборов конкретных высказываний в формулу, получаем истинное высказывание
42. Формула алгебры высказываний называется опровержимой, если:
а) она на любом наборе высказываний, подставляемых вместо пропозициональных переменных, представляет собой ложное высказывание б) существует такой набор высказываний, при подстановке которого в формулу получится ложное высказывание в) существует такой конкретный набор высказываний, при подстановке которого в формулу получается истинное высказывание г) при подстановке любых наборов конкретных высказываний в формулу, получаем истинное высказывание
43. Формула алгебры высказываний называется тождественно ложной, если:
а) она на любом наборе высказываний, подставляемых вместо пропозициональных переменных, представляет собой ложное высказывание б) существует такой набор высказываний, при подстановке которого в формулу получится ложное высказывание в) существует такой конкретный набор высказываний, при подстановке которого в формулу получается истинное высказывание г) при подстановке любых наборов конкретных высказываний в формулу, получаем истинное высказывание
44. Формула алгебры высказываний называется тавталогией, если:
а) она на любом наборе высказываний, подставляемых вместо пропозициональных переменных, представляет собой ложное высказывание б) существует такой набор высказываний, при подстановке которого в формулу получится ложное высказывание в) существует такой конкретный набор высказываний, при подстановке которого в формулу получается истинное высказывание г) при подстановке любых наборов конкретных высказываний в формулу, получаем истинное высказывание
45. Каким из ниже перечисленных слов следует заменить символ а) правила вывода. б) аксиомы в) алфавит г) формулы
46. Каким из ниже перечисленных слов следует заменить символ а) правила вывода. б) аксиомы. в) алфавит. г) формулы.
47. Каким из ниже перечисленных слов следует заменить символ а) правила вывода. б) аксиомы. в) алфавит. г) формулы. 48. Каким из ниже перечисленных слов следует заменить символ Формальная теория включает множество отношений R на множестве формул, которые образуют
а) правила вывода. б) аксиомы. в) алфавит. г) формулы.
49.Каким из ниже перечисленных слов следует заменить символ Выводом формулы F из множества формул Г называется последовательность формул В1, В2, … , Вк, Вк+1, … , Вn = F, где каждая формула Вк есть либо формула из Г, либо
а) аксиома б) тождество в) теорема г) слово
50.Каким из ниже перечисленных слов следует заменить символ Выводом формулы F называется последовательность формул В1, В2, … , Вк, Вк+1, … , Вn = F, где каждая формула Вк есть либо
а) формула б) тождество в) теорема г) аксиома
51. Правило Modus Рonenc имеет вид:
а) б) в) г)
52. Правило Modus tollens имеет вид:
а) б) в) г) 53. Каким из ниже перечисленных слов следует заменить символ Метатеория – это совокупность фактов о свойствах теории, в частности, факт выводимости некоторой формулы теории является а) теоремой. б) метатеоремой. в) аксиомой. г) леммой.
54. Полнота Формального исчисления высказываний (ФИВ) означает: а) что существует эффективное правило или алгоритм доказательства теорем. б) что ни одна из аксиом этой теории не выводится из остальных в) что всякая выводимая в ФИВ формула является тавтологией содержательной теории высказываний и всякая тавтология должна выводиться в ФИВ: г) что в ней невозможно доказать обе формулы F и
55. Разрешимость Формального исчисления высказываний (ФИВ) означает: а) что существует эффективное правило или алгоритм доказательства теорем. б) что ни одна из аксиом этой теории не выводится из остальных в) что всякая выводимая в ФИВ формула является тавтологией содержательной теории высказываний и всякая тавтология должна выводиться в ФИВ: г) что в ней невозможно доказать обе формулы F и
56. Независимость системы аксиом Формального исчисления высказываний (ФИВ) означает: а) что существует эффективное правило или алгоритм доказательства теорем. б) что ни одна из аксиом этой теории не выводится из остальных в) что всякая выводимая в ФИВ формула является тавтологией содержательной теории высказываний и всякая тавтология должна выводиться в ФИВ: г) что в ней невозможно доказать обе формулы F и
57. Непротиворечивость Формального исчисления высказываний (ФИВ) означает: а) что существует эффективное правило или алгоритм доказательства теорем. б) что ни одна из аксиом этой теории не выводится из остальных в) что всякая выводимая в ФИВ формула является тавтологией содержательной теории высказываний и всякая тавтология должна выводиться в ФИВ: г) что в ней невозможно доказать обе формулы F и
58. Какая из приведенных формул не выводима в Формальном исчислении высказываний а) б) в) г)
59. Какая из приведенных формул не выводима в Формальном исчислении высказываний а) б) в) г)
60. Какая из приведенных формул выводима в Формальном исчислении высказываний а) б) в) г)
Часть 4 Логика предикатов 61. Каким из ниже перечисленных слов или сочетанием слов следует заменить символ n-местный предикат – это определённое на множестве а) высказывание. б) аксиому. в) пропозициональную переменную. г) булевскую переменную.
62.Если при любой подстановке вместо переменных а) тождественно-ложным б) тождественно-истинным в) выполнимым г) опровержимым 63.Если при любой подстановке вместо переменных из а) тождественно-ложным. б) тождественно-истинным. в) выполнимым. г) опровержимым.
64. Предикат а) высказывание. б) формулу. в) истинное высказывание. г) известное высказывание.
65. Предикат а) ложное высказывание. б) формулу. в) истинное высказывание. г) известное высказывание.
66. Каким из ниже перечисленных слов или сочетанием слов следует заменить символ Операцией связывания кванторов общности называется правило, по которому каждому одноместному предикату P(x), определенному на множестве М сопоставляется высказывание . : а) выполнимым предикатом. б) опровержимым предикатом. в) тождественно-истинным предикатом. г) известным высказыванием.
67 Каким из ниже перечисленных слов или сочетанием слов следует заменить символ Операция связывания кванторов существования называется правило, по которому каждому одноместному предикату P(x), определенному на множестве М сопоставляется высказывание а) выполнимым предикатом. б) тождественно ложным предикатом. в) опровержимым предикатом. г) истинным высказыванием.
68. Каким из ниже перечисленных слов или сочетанием слов следует заменить символ Операцией связывания кванторов общности по переменной а) тождественно-истинным. б) опровержимым предикатом. в) выполнимым. г) тождественно ложным предикатом.
69 Операцией связывания кванторов существования по переменной а) тождественно-истинным. б) опровержимым предикатом. в) выполнимым. г) тождественно ложным предикатом:
70. В формуле а) первой. б) связанной. в) свободной. г) существующей.
71. В формуле а) первой. б) связанной. в) свободной. г) общей.
72. В формуле а) второй б) связанной. в) свободной. г) существующей.
73. В формуле а) второй б) связанной. в) свободной. г) общей.
74: Предикат ln(x²+y³)=21,5, где х, у –действительные числа, является а) тождественно истинным б) тождественно ложным в) выполнимым г) тавтологией
75. Предикат x²+y²= -11, где х, у –действительные числа, является а) тождественно истинным. б) тождественно ложным. в) выполнимым г)опровержимым
76: Предикат ln(x²+y³)=21,5, где х, у –целые числа, является а) тождественно истинным б) тождественно ложным в) выполнимым г) тавтологией
77. Предикат x²+y²= -11, где х, у –комплексные числа, является а) тождественно истинным. б) тождественно ложным. в) выполнимым г)опровержимым
78. Предикат «Формальная теория высказываний является x» где x есть одно из понятий множества {формальная теория, полная теория, разрешимая теория, непротиворечивая теория} является а) тождественно истинным. б) тождественно ложным. в) 2-местным г)опровержимым
79. Предикат «Формальная теория предикатов является x» где x есть одно из понятий множества {формальная теория, полная теория, разрешимая теория, непротиворечивая теория} является а) тождественно истинным. б) тождественно ложным. в) 4-местным. г) выполнимым
80. Формула а) замкнутой. б) открытой. в) высказыванием. г) матрицей.
Раздел 5 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2024 stydopedia.ru Все материалы защищены законодательством РФ.
|
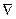в предложении: Формальная теория включает множество символов А, образующих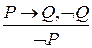 
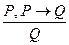
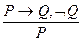
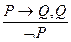
F.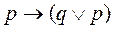
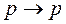
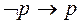
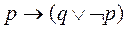
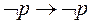
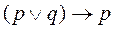
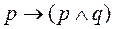
функция, которое при подстановке вместо элементов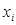 
из множества 
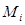обращается в 
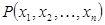, заданный на множестве 
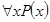, которое истинно тогда и только тогда, когда P(x) является 
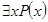, которое ложно в том и только том случае, когда P(x) является 
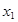называется правило, по которому каждому n-местному предикату 
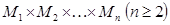сопоставляется (n-1)-местный предикат 
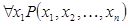, определенный на множестве 
, который на любых наборах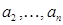 
превращается в высказывание 
, истинное в том и только том случае, когда одноместный предикат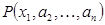 
, определенный на множестве 
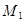, является 
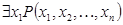, определенный на множестве 
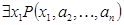, ложное в том и только том случае, когда одноместный предикат 
называется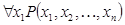
переменная 
называется