
|
|
Давление в покоящейся жидкостиГидростатика. Давление в покоящейся жидкости Уравнение равновесия жидкости, находящейся в относительном покое, в дифференциальной форме имеет вид:
Основное уравнение гидростатики может быть представлено так:
Гидростатическое давление в точке определяется по формуле:
Гидростатическое давление может быть условно выражено высотой столба жидкости Величина давления Разница между полным давлением и атмосферным называется манометрическим давлением: Вакуумом называется недостаток давления до атмосферного:
Сила давления покоящейся жидкости на плоские стенки Сила суммарного давления жидкости на плоскую стенку равна произведению смоченной площади стенки на гидростатическое давление в центре тяжести этой площади:
Центр давления – точка приложения равнодействующей сил давления –определяется формулой:
где
Сила давления жидкости на криволинейные стенки Равнодействующая сила давления жидкости на цилиндрическую поверхность равна:
где
Направление равнодействующей силы давления на криволинейную поверхность определяется через составляющие:
Плавание тел Условие плавания тел определяется неравенством:
где Здесь W – водоизмещение плавающего тела. Плавание будет остойчивым, если выполняется условие:
где
Метацентрический радиус находится по формуле:
где
Примеры решения задач. Давление в покоящейся жидкости Пример 2.1. Определить избыточное давление в забое скважины глубиной h=85 м, которая заполнена глинистым раствором плотностью ρ=1250кг/ м Решение. Величину избыточного давления находим по формуле p=ρgh= Ответ: p= 1МПа.
Пример 2.2. Определить избыточное давление воды в трубе по показаниям батарейного ртутного манометра. Отметки уровней ртути от оси трубы: z Решение. Батарейный ртутный манометр состоит из двух последовательно соединенных ртутных манометров. Давление воды в трубе уравновешивается перепадами уровней ртути, а также перепадами уровней воды в трубках манометра. Суммируя показания манометра от открытого конца до присоединения его к трубе, получим:
где
Подставляя исходные величины, получим:
Ответ:
Пример 2.3. Нижняя часть рабочей камеры кессона находится на глубине h=30м от свободной поверхности воды. Определить избыточное и абсолютное давление воздуха, которое необходимо создать в рабочей камере кессона, чтобы вода из реки не могла проникнуть в камеру. Решение. Избыточное давление воздуха в рабочей камере должно быть не менее гидростатического давления на заданной глубине, т.е.
Абсолютное давление в рабочей камере кессона найдем по формуле
Ответ:
Пример 2.4. Определить тягу Решение. Давление в топке на уровне сечения 2-2 составит
где
Давление перед топочной дверкой на уровне сечения 2-2
где Давления дымовых газов и воздуха равны
Разность давлений в топке котла и перед топочной дверкой равна
или
Принимаем:
Вычислим разность напоров
Пример 2.5. Колокол 1 газгольдера диаметром D=6,6 м весит Решение. Для обеспечения равновесия колокола сила суммарного давления газа Р на верхнее перекрытие колокола должна быть равна весу колокола G , т.е.Р=G. В то же время сила суммарного давления на воду под колоколом составляет
где
Вычисляем площадь сечения колокола
и получаем
Давление Следовательно,
и разность уровней Н составляет
Ответ: Н=0,102 м.
Пример 2.6. Определить давление в резервуаре Решение. Условие равновесия для ртутного манометра можно записать в следующем виде:
где
Найдем давление p0 в газовой подушке
Таким образом, в резервуаре – вакуум, величина которого составит
Запишем условие равновесия для трубки 1
откуда найдем высоту подъема уровня воды в трубке 1
Ответ: Пример 2.7. Для заливки центробежного насоса 1 установлен вакуумнасос 2. Какой необходимо создать вакуум в камере рабочего колеса насоса, если верх корпуса центробежного насоса находится над уровнем воды в резервуаре на расстоянии Н=3,5м? Решение. Из формулы для нахождения вакуума
где
Ответ: Задачи к разделу. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
 .
. .
. .
. .
. = 1 кг/см2 = 9,81∙104 Па называется технической атмосферой. Давление, равное одной технической атмосфере, эквивалентно давлению столба воды высотой 10 м.
= 1 кг/см2 = 9,81∙104 Па называется технической атмосферой. Давление, равное одной технической атмосфере, эквивалентно давлению столба воды высотой 10 м. .
.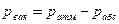 .
.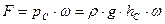 .
. ,
, – заглубление центра тяжести смоченной площадки под уровень свободной поверхности;
– заглубление центра тяжести смоченной площадки под уровень свободной поверхности; – момент инерции смоченной площади относительно оси, проходящей через центр тяжести площади параллельно линии уреза жидкости.
– момент инерции смоченной площади относительно оси, проходящей через центр тяжести площади параллельно линии уреза жидкости. ,
, – горизонтальная составляющая полной силы гидростатического давления на криволинейную поверхность;
– горизонтальная составляющая полной силы гидростатического давления на криволинейную поверхность; – вертикальная составляющая полной силы гидростатического давления на криволинейную поверхность, равная весу жидкости в объеме тела давления.
– вертикальная составляющая полной силы гидростатического давления на криволинейную поверхность, равная весу жидкости в объеме тела давления. .
.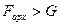 ,
,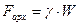 .
. ,
, – метацентрический радиус;
– метацентрический радиус; – расстояние между центром тяжести тела и центром водоизмещения.
– расстояние между центром тяжести тела и центром водоизмещения. ,
, – водоизмещение.
– водоизмещение. .
. Па
Па  1МПа.
1МПа. =1,75 м ; z
=1,75 м ; z  = 3 м ; z
= 3 м ; z  = 1,5 м ; z
= 1,5 м ; z  = 2,5 м.
= 2,5 м. 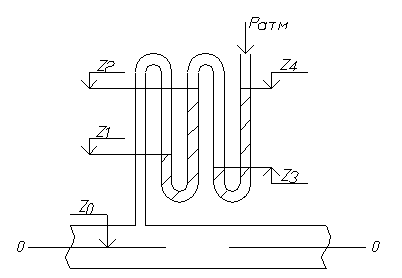
 ,
, 
 =1000
=1000  - плотность воды;
- плотность воды; - плотность ртути.
- плотность ртути.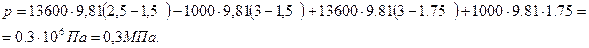

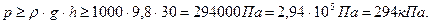
 т.е.
т.е.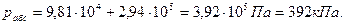
 .
.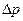 (разность давлений) в топке котла и перед топочной дверкой Д , если высота котла и дымовой трубы Н=15м. Дымовые газы имеют температуру t
(разность давлений) в топке котла и перед топочной дверкой Д , если высота котла и дымовой трубы Н=15м. Дымовые газы имеют температуру t  Температура наружного воздуха
Температура наружного воздуха  .
.
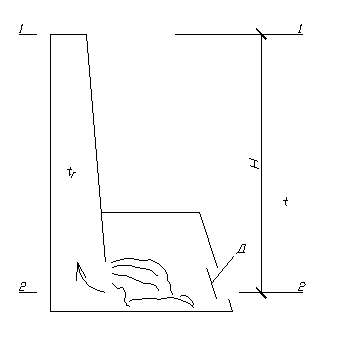
 атмосферное давление на уровне сечения 1-1;
атмосферное давление на уровне сечения 1-1;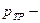 давление, создаваемое дымовыми газами, удаляемыми через трубу.
давление, создаваемое дымовыми газами, удаляемыми через трубу.
 давление, создаваемое столбом воздуха высотой Н.
давление, создаваемое столбом воздуха высотой Н. ; где
; где  ,
,  ,
, - плотность газа при температуре
- плотность газа при температуре  ;
;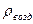 - плотность воздуха при температуре
- плотность воздуха при температуре  .
.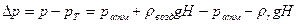
 .
. и
и 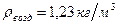 . Тогда получим:
. Тогда получим: .
.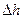 ;
; ;
; м вод. ст.
м вод. ст. . Определить разность Н уровней воды под колоколом газгольдера и в его стакане 2.
. Определить разность Н уровней воды под колоколом газгольдера и в его стакане 2.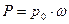
 - давление газа под колоколом;
- давление газа под колоколом; - площадь колокола.
- площадь колокола.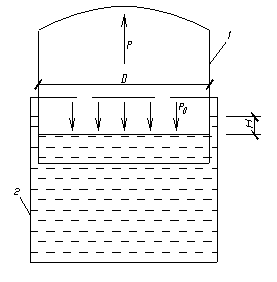 Из сравнения упомянутых зависимостей найдем давление в газовой подушке колокола
Из сравнения упомянутых зависимостей найдем давление в газовой подушке колокола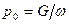 .
. 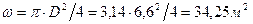
 .
. ,действующее на поверхность воды под колоколом, должно быть уравновешено разностью уровней воды Н.
,действующее на поверхность воды под колоколом, должно быть уравновешено разностью уровней воды Н.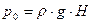
 .
. в трубке 1, если показания ртутного манометра
в трубке 1, если показания ртутного манометра  и
и  .
. ,
, - плотность ртути;
- плотность ртути;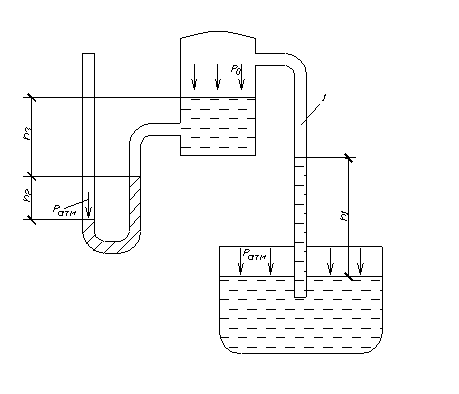
 .
.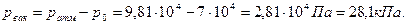
 ,
, .
.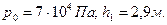
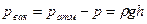 имеем:
имеем: ,
, - абсолютное давление на поверхности воды в корпусе насоса после его заливки;
- абсолютное давление на поверхности воды в корпусе насоса после его заливки; 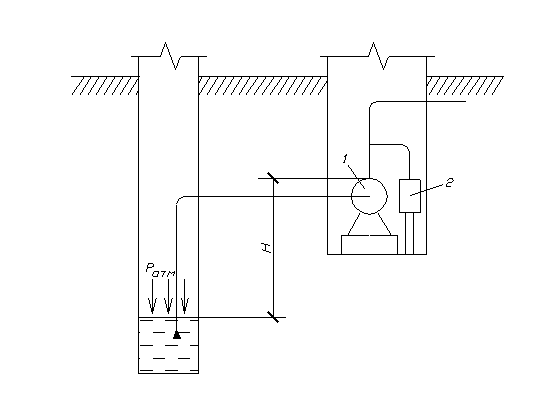
 .
. .
.